np -165　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　ベルヌーイ　( スイス )　 　　　　　　１８ 世 紀　　　　　　　 ベツセル　( ドイツ )


　　　　　　　　　ダニエル・ベルヌーイ　は　13 歳 で 大 学　1５ 歳 で 学士試験合格 1６ 歳 で 修士号 取 得

　　　　　　　　　　　　　　　　　　　　　　　　父　兄　弟　本人　皆　　学 者


　　　　　　　　　ベッセル関数　Bessel function　とは、最初にスイスの数学者　ダニエル・ベルヌーイ　によって定義され　
　　　　　　　　　フリードリヒ・ヴィルヘルム・ベッセルにちなんで名づけられた関数。 円 筒 関 数 と呼ばれる。

　　　　　　　　　以下に示す、ベッセルの 微分方程式 における${\displaystyle y(x)}$　 特殊解 の1つである


　　　　　　　　　　　　　


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

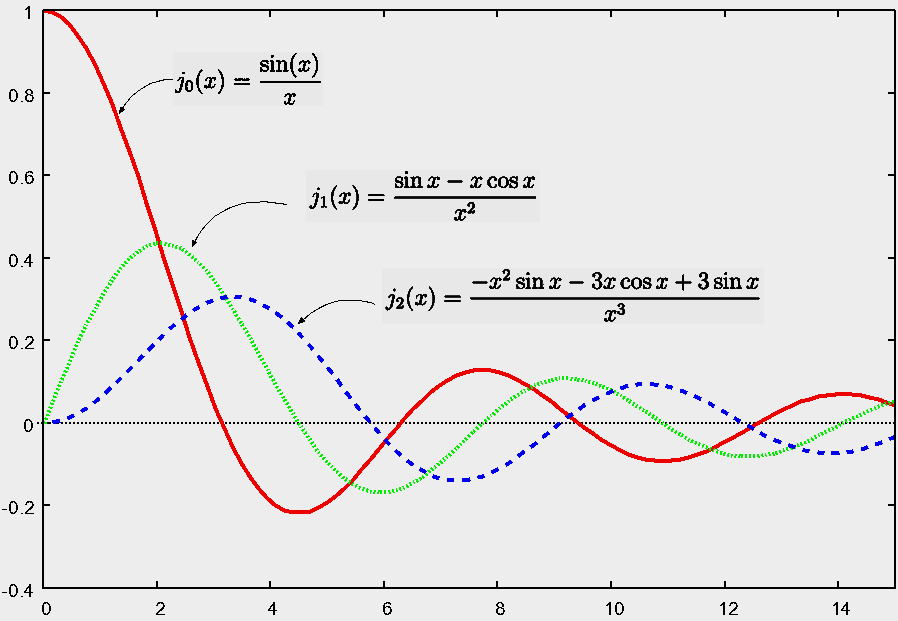
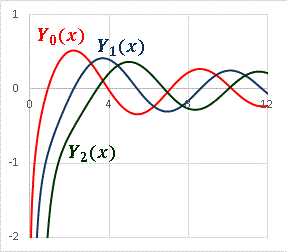
　　　　　　　　　　　　　　　　　　　　　第 １ 種　ベツセル関数　グラフ　　　　　　　　　　第 ２ 種　ベツセル関数　グラフ


　　　　　　　　　　　第Ⅰ種 ベツセル 関 数　グラフ　高 精 度 計 算　　　　CASIO

　　　　　　　　　　　　　　Bessel function of the 1st kind 　J_^ν ( x )

　　　　　　　　　　( 1 )　　x ² y" + x y´ + ( x ² - ν² ) y 　= 　o　　　y 　=　 J_^ν ( x )

　　　　　　　　　　( 1 )　　J_^ν ( x ) 　= 　Σ_k=0 ^∞ 【 (-1 ) ^k / k ！Γ( k + ν+ 1 ) 】 ( x / 2) ^{ν+ 2k}

　　　　　　　　　　( 1 )　　e ^{( x / 2 ) ( t - 1 / t )} = 　Σ_k=0 ^∞ 【 Jn ( x ) tⁿ　　　n 　=　 integer　


　　　　　　　　　　　　　　第２種 ベツセル 関 数　グラフ　高 精 度 計 算
　　　　
　　　　　　　　　　　　　　Bessel function of the ２nd kind 　Y_^ν ( x )

　　　　　　　　　　 ( 1 )　　x ² y" + x y´ + ( x ² - ν² ) y 　= 　o　　　y 　=　 _^Yν ( x )

　　　　　　　　　 　( 1 )　　_^Yν ( x ) 　=　 J_^ν ( x ) cos ( νπ) - J_^-ν ( x )

　　　　　　　　　 　( 1 )　　_^Y-ν ( x )　 =　 (- 1)^{n _Yn} ( x )



　　　　　　　　　　　　　▲　　第 １ 種 　ベツセル　関 数
　
　　　　　　　　　　第 1 種 ベッセル 関 数 は 　${\displaystyle \displaystyle J_{\alpha }(x)}$Jα ( x ) 　と 表 記 される。

　　　 　　　${\displaystyle \displaystyle J_{\alpha }(x)}$Jα ( x ) はベッセルの微分方程式の解であり、${\displaystyle \displaystyle \alpha }$α が整数もしくは非負であるとき、 x = 0${\displaystyle \displaystyle x=0}$で有限の値をとる

。　　 ${\displaystyle \displaystyle J_{\alpha }}$　　Jα における、特定解の選択及び正規化は定義された後に、後述する。

　　　　　　　第1種ベッセル関数はまた、${\displaystyle \displaystyle x=0}$x = 0 のまわりでの　テイラー展開　（非整数の${\displaystyle \displaystyle \alpha }$　α　 に対しては、

　　　　　　　より一般に　べき級数展開　　によって定義することもできる。

　　　　　　　　　

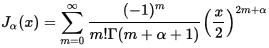
　　　　非整数の ${\displaystyle \displaystyle \alpha }$α に対しては、 ${\displaystyle \displaystyle J_{\alpha }(x)}$Jα ( x ) と ${\displaystyle \displaystyle J_{-\alpha }(x)}$J -α ( x ) とが、ベッセルの微分方程式に対する線形独立な2つの解を与える。

　　　　　　　　整数の${\displaystyle \displaystyle \alpha }$ に対してはこれらは線形独立な解を与えない。

　　　　　　　　なぜなら、整数${\displaystyle \displaystyle n}$ に対して、 ${\displaystyle \displaystyle J_{n}(x)}$Jα ( x ) と ${\displaystyle \displaystyle J_{-\alpha }(x)}$J -α ( x ) と ${\displaystyle \displaystyle J_{-n}(x)}$の　あいだには　関 係

　　　　　　　　　　${\displaystyle \displaystyle J_{-n}(x)}$

${\displaystyle \displaystyle J_{-n}(x)=(-1)^{n}J_{n}(x)}$

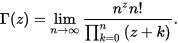
　　　　が成り立ち、両者は明らかに　線形従属　となるからである。

　　　　　　整数次数に対して ${\displaystyle \displaystyle J_{n}(x)}$Jα ( x ) と　線形独立な第二の解　は、以下の第2種ベッセル関数によって与えられる

　　　　　　　　　第Ⅰ種 ベツセル 関 数　グラフ　高 精 度 計 算　　　　CASIO

　　　　　　　　　　　　　　Bessel function of the 1st kind 　J_^ν ( x )

　　　　　　　　　　( 1 )　　x ² y" + x y´ + ( x ² - ν² ) y 　= 　o　　　y 　=　 J_^ν ( x )

　　　　　　　　　　( 1 )　　J_^ν ( x ) 　= 　Σ_k=0 ^∞ 【 (-1 ) ^k / k ！Γ( k + ν+ 1 ) 】 ( x / 2) ^{ν+ 2k}

　　　　　　　　　　( 1 )　　e ^{( x / 2 ) ( t - 1 / t )} = 　Σ_k=0 ^∞ 【 Jn ( x ) tⁿ　　　n 　=　 integer　


　　　　　　　　　　　　　　第２種 ベツセル 関 数　グラフ　高 精 度 計 算
　　　　
　　　　　　　　　　　　　　Bessel function of the ２nd kind 　Y_^ν ( x )

　　　　　　　　　　 ( 1 )　　x ² y" + x y´ + ( x ² - ν² ) y 　= 　o　　　y 　=　 _^Yν ( x )

　　　　　　　　　 　( 1 )　　_^Yν ( x ) 　=　 J_^ν ( x ) cos ( νπ) - J_^-ν ( x )

　　　　　　　　　 　( 1 )　　_^Y-ν ( x )　 =　 (- 1)^{n _Yn} ( x )


　　　　　　　　　　▲　　第 ２ 種 　ベツセル　 関 数

　　　　　　　　　第 2 種 ベッセル 関 数は　 ${\displaystyle \displaystyle Y_{\alpha }(x)}$Y α ( x ) 　と 表 記 される

　　　　 ${\displaystyle \displaystyle Y_{\alpha }(x)}$Y α ( x ) 　はやはり　ベッセルの微分方程式の解　であり、

　　　　${\displaystyle \displaystyle x=0}$x = 0 において特異性をもつ。また、${\displaystyle \displaystyle Y_{\alpha }(x)}$Y α ( x ) は、しばしばノイマン関数とも呼ばれ、${\displaystyle \displaystyle N_{\alpha }(x)}$N α ( x ) とも表記される。

　　　　第1種　ベッセル関数 　${\displaystyle \displaystyle J_{\alpha }(x)}$J α ( x ) 　との関係　は

　　　　　　　　　　　

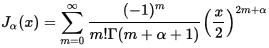
　　で与えられる。ただし、${\displaystyle \displaystyle \alpha }$α が 整 数 のときは 右 辺 は 極 限 によって　定 義 されるものとする。

非整数 の ${\displaystyle \displaystyle \alpha }$α に対しては、 ${\displaystyle \displaystyle J_{\alpha }(x)}$J α ( x ) と ${\displaystyle \displaystyle J_{-\alpha }(x)}$J -α ( x ) と${\displaystyle \displaystyle J_{-\alpha }(x)}$が 線形独立 な 2 つ の 解 をすでに与えているので、

${\displaystyle \displaystyle Y_{\alpha }(x)}$

Y α ( x ) は 解 の表現としては冗長である。

整 数 ${\displaystyle \displaystyle n}$n 　に対しては、${\displaystyle \displaystyle Y_{n}(x)}$は${\displaystyle \displaystyle J_{n}(x)}$と　線形独立な第二の解　を与えている。

整 数 ${\displaystyle \displaystyle n}$n に対して、${\displaystyle \displaystyle Y_{n}(x)}$Y α ( x ) 　と　 ${\displaystyle \displaystyle Y_{-n}(x)}$Y - α ( x ) 　とのあいだには 関 係


　　　　　　　　　　　　　　　　

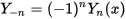
が 成り立ち、したがって両者は やはり 線 形 従 属 である。

${\displaystyle \displaystyle J_{\alpha }(x)}$J α (x ) 及び ${\displaystyle \displaystyle Y_{\alpha }(x)}$はどちらも、負の実軸を除く複素平面上で x ${\displaystyle \displaystyle x}$の解析的な関数（正則な関数）である。　　　　

${\displaystyle \displaystyle \alpha }$

x 　が　正の整数のとき、これらの関数は負の実軸上に分岐点を持たず、したがって ${\displaystyle \displaystyle x}$x の整関数となる。

また、固 定 した ${\displaystyle \displaystyle x}$　x　 に対して、ベッセル　関 数　α　の　整 関 数

　　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー