np -175　　　　　　

　　　　　　　　　　　　　●　　　　　ベーター　関　数


　　　　　　　　　　　　　ベータ 関 数　 beta function）　　と　は


　　、ルシャンドル の 定 義　に従って　　第一種オイラー積分　　とも呼ばれる 　特 殊 関 数 である



　　　　　　　　 　　　　　　　　　　　　　　　　　　β　関 数　　高 精 度 計 算


　　　　　　　　　　　


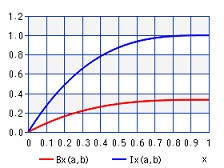
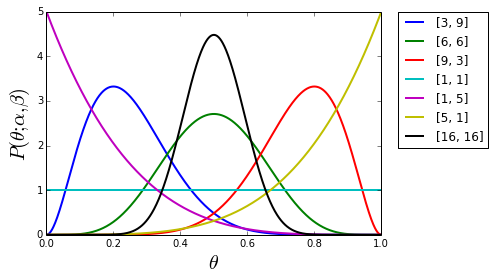
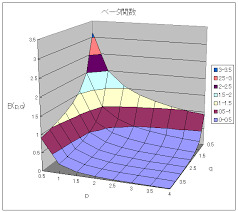
　　　　　　　　　　　B ( x , y )　 =　 ∫ _o¹t^x-1 (1 - t) ^y-1 d t


　　　　　　　　変 数 変 換 　した　積 分 表 示
　　　　　　　　　　

　　　　　　　　　　　　　　　　　B ( x 、 y ) 　= 　2 ∫ ₀^π/2　sin^2x-1 θ　cos^2y-1θ dθ${\displaystyle \mathrm {\mathrm {B} } (x,y)=2\int _{0}^{\pi /2}\sin ^{2x-1}\theta \cos ^{2y-1}\theta \,d\theta \!}$　　　　

　　　　　　　　　　　　　　　　　B ( x 、 y ) 　= 　2 ∫ ₀^π/2　t^x-1 / 【 (t + 1)^{x + y}　】 d t
　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　B ( x 、 y ) 　= 　1 / 2^{x + y -1} ∫_-1¹ (1 + t)^x-1(1-t)^y-1 d t　　　　　${\displaystyle \mathrm {\mathrm {B} } (x,y)=\int _{0}^{\infty }{\frac {t^{x-1}}{(1+t)^{x+y}}}\,dt\!}$　　　　　　　　　　　　　${\displaystyle \mathrm {\mathrm {B} } (x,y)={\frac {1}{2^{x+y-1}}}\int _{-1}^{1}(1+t)^{x-1}(1-t)^{y-1}\,dt\!}$　　　　　　　　　　　　　


　　　　　　　　ベータ 関 数　との　関　係


　　　　　　　　　　　　　　　　　ベータ 関 数　は　次 の よ う に　ガンマ 関 数　と 結 び つ く


　　　　　　　　　　　　　　　　　B ( x ・y )　=　【　Γ(x)　Γ(y)　 】 　/ 　Γ (x + y)


　　　　　　　　　　　　　　　　　　例　　　　x　=　1　　 y　=　2　　　　　　答　え　　0.5


　　　　　　　　手　計　算　　　B ( 1 ・2 )　=　【　Γ (1)　Γ(2)　 】 / Γ(1 + 2)　=　1/2　=　0.5

　　　　　　　　　　　　　　　　　　　　　　ガンマ 関 数　を　使つうて　計　算



　　　　　　　　　　　　　　　　　　　　　　次 は　積 分　を　使つて　計　算

　　　　　　　　　　　　　　　　　　B ( 1 ・2 )　=　∫₀¹　 t^a-1 (1-t)^b-1 d t

　　　　　　　　　　　　　　　　　　　　　　　　　　=　∫₀¹　t^1-1　(1-t)^2-1 d t　=　∫₀¹ 　t⁰　 (1-t)¹ d t
　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　=　∫₀¹ 　 (1-t) d t　=　1/2　=　0.5



　　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー