 np -180
np -180 
パスカルの三角形 出 典: フリー百科事典 『ウィキペディア(Wikipedia)』
 二 項 定 理 の 係 数
二 項 定 理 の 係 数

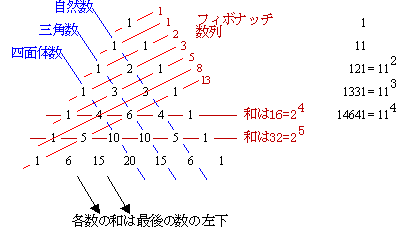
パスカルの三角形 (英語:Pascal's triangle)は、二 項 展 開 における 係 数 を 三 角 形 状 に並べたものである。
ブレ ーズ・パスカル(1623年 - 1662年)の 名前がついているが、実際には パスカル より 何世紀も前 の数学者たちも研究していた。
この三角形の作り方は単純なルールに基づいている。まず最上段に1を配置する。それより下の行はその位置の右上の数と
左上の数の和を配置する。例えば、5段目の左から2番目には、左上の1と右上の3の合計である4が入る。このようにして数を並べると、
上から n 段目、左から k 番目の数は、二項係数
( n - 1) C k - 1 = ( n - 1 ) 階 乗 / ( ( k - 1 ) 階 乗 ) ・ (( n - 1 ) - ( k - 1 )) 階 乗
負でない 整数 n ≥ k に対して
n C k = n - 1 C k - 1 + n - 1 C k
n C o = 1
が成り立つ。
パスカルの三角形は三次元以上に拡張が可能である。3次の物は 「パスカルのピラミッド」 「パスカルの四面体」 と呼ばれる。
4次以上のものは一般に 「パスカルの単体」 と呼ばれる。
( a + b ) 2 = a 2 + 2 a b + b 2
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
( a + b ) 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 a b 3 + b 4
二 次 ・ 三 次 ・ 四 次 方 程 式 の 解 の 導 出 の 展 開 式 において 変 数 変 換 が おこなわれる
これらの 公 式 を 暗 記 しておくと 便 利 で あ る
--------------------------------------------------------
参 考 おもしろい 数 列 を 見 つ け ま し た
自 然 数 1 2 3 4 5 6 7 8 -------
三 角 数 1 3 6 10 15 21 28 36 …
自 然 数 の n 番 目 ま で を 足 し た 数 を n 番 目 の 項 とする
三 角 推 数 1, 4, 10, 20, 35, 56, 84, 120, 165
三 角 数 の n 番 目 ま で を 足 し た 数 を n 番 目 の 項 とする
- 四 面 体 数 1 4 10 20 35
三 角 推 数 と 同 じ
図 形 数 平 方 数 四 角 数 1 4 9 16 25
- ● 自 然 数 1 2 3 4 5 6 7 ---
-
- ● 三 角 数
デジタル大辞泉の解説
等差数列 で 、自 然 数 の 等 差 数 列 1,2,3,4,5,6… の 第 n 項 までの 和 を 第 n 項
と する 数 列 1,3,6,10,15,21…。また、その 各 項。
1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
1+2+3+4+5+6=21 … となる。
第 n 項 の 三 角 数 は n (n+1) ÷ 2 で 表 す こ と が できる。
y = Σ1 n n ( n + 1 ) ÷ 2
三 角 数 の グ ラ フ
●
三 角 推 数 と は
三 角 錐 数 triangular pyramidal number)は 球 を 右 図 のように 三 角 錐 の 形 にならべたとき、
そこに含まれる 球 の 総 数 にあたる 自 然 数 である。
つまり 三 角 数 を 1 から小さい順に 足した数 の ことである。 四面体数 (しめんたいすう、

例: 1, 4 (=1+3), 10 (=1+3+6), 20 (=1+3+6+10), 35 (=1+3+6+10+15)
n 番目の 三角錐数 Tn は1から n 番目 の 三角数 n(n + 1)/2 までの 和 に等しいので
また組み合わせの記号を用いると となる。
三角錐数 を 小さい順 に 列 記 すると
- 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969,
● 四 面 体 数 1 4 10 20 35
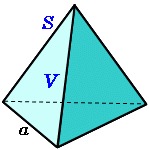

整 数 : n
三 角 数 : n(n+1)/2
四 面 体 数 : n(n+1)(n+2)/6
5 胞 体 数 : n(n+1)(n+2)(n+3)/24 五 砲 体 数 とは
ここでは, シェルピンスキー の 論文 にしたがって, 四面体数 の 性 質 について考えてみる.
161^2-360・72 = 1 より,
an+1 = 161an+360bn, bn+1 = 72an+161bn
a1 = 9 , b1 = 4 とする.
an+1 = 161an+360bn = 161an+360(72an-1+161bn-1)
= 161an-an-1+161(161an-1+360bn-1) = 161an+160an-1
bn+1 = 72an+161bn = 72(161an-1+360bn-1)+161bn
= 161(72an-1+161bn-1)+161bn-bn-1 = 161bn+160bn-1 より
an+1 = 161an+160an-1,bn+1 = 161bn+160bn-1
α,βを2次方程式x^2-161x-160 = 0 の根として,
an+1-αan = β(an-αan-1) β^2(an-1-αan-2) = ・・ = β^(n-1)(a2-αa1)
α,βを入れ替えると
an+1-βan = α^(n-1)(a2-βa1)
an+1-αan = β^(n-1)(a2-αa1)
したがって,整数列{an}の一般項は
an = {α^(n-1)(a2-βa1)-β^(n-1)(a2-αa1)}/(α-β)
整数列{bn}でも同じ漸化式ですから,同じ一般項になります.
bn = {α^(n-1)(b2-βb1)-β^(n-1)(b2-αb1)}/(α-β)
===================================
ところで,
(161a+360b)^2-5(72+161b)^2 = a^2-5b^2 より,
α^n = an+bn√5
β^n = an-bn√5
を満足させるような整数列{an},{bn}になっています.
これらの数列は
an^2-5bn^2 = 1
となる関係式で結ばれていて,
an/bn→ √5
ですから, √5 に最も近い分数を与えることがわかります(最良近似).
● 図 形 数 平 方 数 四 角 数 1 4 9 16 25 36
図形数 (figurate numbers) とは、一定の規則 で 図形状 に並べられた点の
個数として表される 自然数 の 総称 である。
その歴史は、古代ギリシアのピタゴラス学派が「万物は数である」との思想のもと、
図形と数を結び付けたところにまで遡る。例えば、図形として 正方形 を考えると、
数としては 平方数 を得る。平方数を図形数として見るときには、これを特に「四角数」と呼ぶ
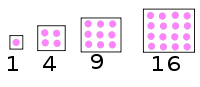

↑ ↑
n 2 → 1 2 2 2 3 2 奇 数 の 和 1 + 3 + 5 + 7 = 16


三 角 数 の 2 倍 は 矩 形 数 三角数 の 8 倍 に 1 を加えると 四角数
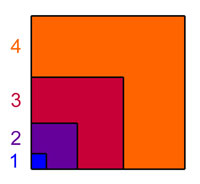
+ 23 + 33 + 43 = (1 + 2 + 3 + 4) 2 を示す図
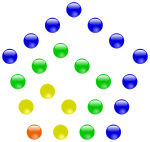
五 角 数 各グノモンの 面 積 は 立 方 数 である

五 角 数 ア ニ メ
===================================
● フィポナツチ 数 列
フィボナッチは次の問題を考案した[3]。
- 1つがいの兎は、産まれて2か月後から毎月1つがいずつの兎を産む。
- 兎が死ぬことはない。
- この条件のもとで、産まれたばかりの1つがいの兎は1年の間に何つがいの兎になるか?
つがいの数は次の表のようになる。どの月のつがいの合計も、
その前の2つの月での合計の和となり、フィボナッチ数が現れていることがわかる

 np -180
np -180