
 np - 208
np - 208
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
数 学 史 の 偉 業 論 文 掲 載 へ 2020 04 04 読売新聞


京 都 大 は 3 日、数 学 の 未 解 決 難 問 A B C 予 想 の 証 明 に 成 功 したとする
京大 数理解析 研究所 の 望月新一 教 授 ( 51 ) の 論 文 について、国際的 な 数学 専門誌 PRIMS に
掲 載 が 決まつた と 発 表 し た
投 稿 か 7年半 という 異 例 の 時 間 をかけて 他の 数学者 たちが 検 証 し 、正しい と 認 め た
専 門 家 は 数学史 に 残 る 偉 業 と 評 価 している
★ 審 査 7 年 半
A B C 予 想 は 1985 年 に 欧 州 の 二 人 の 数 学 者 が 提 唱
整 数 A , B と 、 それらを 足し合わせた C 間 に 、
か け 算 が 絡 む 特 別 な 関 係 が 成り立つ と 予 想 している
望月教授 は、整 数 論 や 幾 何 学 を 組み合わせた 宇 宙 際 タイヒミュラー 理 論 という
全く 新しい 理 論 を 提 唱
この理論 に 基づくいて A B C 予 想 を 証 明 したとする 4本 の 論 文 を、
2012年8月 に 自身 の ホームページ 上 で 発 表 し、PRIMS に 投 稿 した
全体で 600 ペーイ 以上に及び、あまりにも 独 創 的 な 内 容 から 未 来 から 届いた 論 文 などと 評 された
PRIMS は 数 理 研 が 編 集 し、欧州数学会 が 発 行 する 望月教授 が
編集委員長 を 務めるが、今回 は 本人 が 審 査 に 関与できないように 特別編集委員会 を
設けて 数人 で 審 査 し、2月 に 掲 載 を 認 めた
記者会見 した 特別編集委員長 の 玉川安騎男 教授 は 学 問 的 な 観 点 から 慎 重 に
議 論 を 重ね、証 明 が 正しいと 認 めた と、公正 な 審 査 だつたことを 強 調 した
望月教授 は 19才 で 米プリンストン大 数学科 を 卒 業 し、32才 の 若さ で 京大教授 に
就任した 天才肌 の 数 学 者
メデイア の 取材 に 応じない意向 を 示しており、記者会見 に も 出 席 しなかつた
加藤文元 東京工大教授 ( 数論幾何学 ) の話 望月 教授 の 理 論 は A B C 予 想 の 証明 にとどまらず、
他の数々 の 未解決予想 の 証 明 にもつながると 期 待 される
21 世紀 の 数 学 を 代 表 する 業 績 で、今後 の 数 学 界 への 影 響 は 計り 知れない
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
★ A B C 予 想 Yahoo よ り
35年間 未解決で、世界中 の 数学者 を 悩ませてきた 数学 の 超難問 「ABC予想」 を、京都大数理解析研究所 の
望月新一 教授 (51) が 証 明 した。
2千年以上 の 歴史 がある 整数論 の 中で、「最も重要な未解決問題」 とも言われた 難 題 とは、どういったものだろうか。
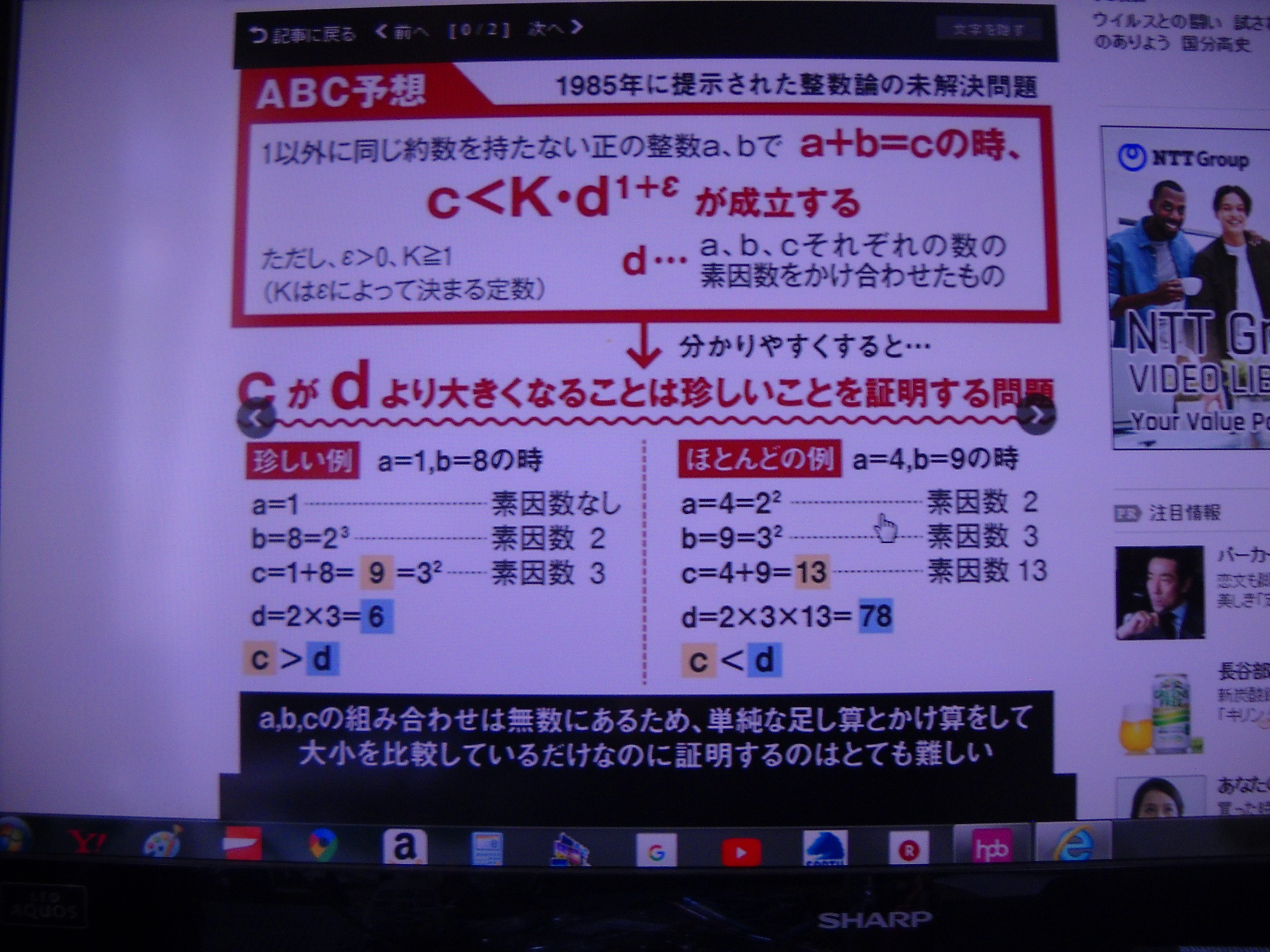
ABC予想は1985年、スイスのデビッド・マッサー氏とフランスのジョゼフ・オステルレ氏により提示された 整数論 の 難 問 だ。
それは、a+b=c という 単純な足し算 から 始まる。正の 整 数 a と 整 数 b の 「和」 である c と、三つの数 a、b、c
それぞれの 素 因 数 の 「積」 を考えた時、和 と 積 の 間 に、ある特別な 関 係 があることを示している。
具 体 的 に a = 1 、 b = 8 で 考えると、 a と b の 和 は 「 1+ = 9 (c) 」 となる。
次 に 、b = 8 は 「 2×2×2 」 と 素 因 数 分 解 できるので 素 因 数 は 2 。
同 様 に c = 9 は 「 3×3 」 で 素 因 数 は 3 となる 。
a は 1 なので 素 因 数 はない すると、a、b、c それぞれの 素 因 数 の 積 は 「 2×3 = 6 」 となる。
この場合、和 である c = 9 と、積 である 6 を 比べると 和 が 積 より 大きい 。
だが、実は、無 数 に ある a、b、c の 組み合わせ を 試すと、ほとんどで 、積 が 和 より 大きくなる。
ABC 予想 は 和 が 積 より 大きくなるのは とても珍しい、ということを 主 張 している。
単純な 足し算 と かけ算 をして 大 小 を 比 較 しているだけなのに、証 明 するのはとても 難 し い。
整 数 は 1、2、3…… と 無 限 に 続 く 単 純 な 数 だ。だが、実 は、その 整 数 から 導かれる 和 と 積 の
関 係 は
未 解 明 の 部 分 が 多 い。
ABC 予想 は 和 と 積 の 関 係 の 根本的な 部 分 を 明らかにするもので、整数 を 統 制する包括的な 問 題 とされる。
「ABC 予想 が 正しければ……」 と、ABC 予想 を 前 提 とした 研究 は 数多くある。
影 響 の 大きさから、いわば 整 数 を 牛耳る 「 番 頭 」 のような 存 在 なのだ。
ABC 予想 はこうした 影響力 の 大きさから、2 千年 以上 の 歴史 がある 整数論 の 中で 「 最も重要な 未解決問題 」
と
言 われて い た。
ABC 予 想 が 証 明 されると、スピロ 予想 や フライ 予想 、ボイタ 予想 などさまざまな 数 学 の 難 問 が
一挙 に 解 決 すると される。
証 明 に 350 年 以上 かかった 「 フェルマー の 最 終 定 理 」 も、ABC 予想 を 発 展 させると、
数 ページ で 簡 単 に 証 明 できてしまう ほどだ。 ( 石倉徹也 )
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
★ A B C 予 想 の 具 体 例




ABC 予想とは?
ABC 予想 を 一文で書いてしまうと、「 a+b = c が 成り立つ 自然数 ( 正の整数 ) a、b、c において、
積 abc の 素因数 の 関 係 を 考えた時、
数 ( a、b、c ) は いくつかの 組しかない」 ことを 表 し た 予 想 です。
文章 だけだと、ちょっと 分かり にくいかも。
中高生 が 習うような 「 整 数 の 方程式 」 の考え方を ”めちゃくちゃ” 発 展 させたものが、
1985年に 欧 州 の 数学者 ( D・マッサーとJ・オステルレ ) によって 提 唱 されたことから 始まりました。
問 題 の 内 容
(ABC 予 想 を 考える際には、数 ( a、b、c ) を 「 1 以外に 共通 の 約 数 をもたない 『 素 』」 であることが 前 提 です)
a + b = c を 満たす 数 があるとき 、 abc の 積 を d とします。
このとき、a、b、c は 互いに 異なる 数 でなくては いけません。
その d を、任 意 の 実 数 κ ( κ > 1 ) で 累 乗 します。
このとき、普通に考えれば、d は a ~ c のどの 数 よりも 大きくなるものだと 思われますが、
d が c より 小さく なってしまう ことが 稀 に あるのです。
累 乗・・・a の 3 乗 ( a×a×a=a^3 ) みたいなもの
“ abc を 掛け合わせて 出した 数 ” である 「 d 」 が、” もともとあった ” 「 c 」 より 小さく なってしまうと いうことは、
数 組 み 合 わ せ が 無 限 にあると 考えられません。
つまり、ここに挙げられている 数 の 組 ( a、b、c ) は 「 数える程度 」 しか 存在しないのではないか……? と
考えられているのが、 この 「 ABC 予 想 」 なんです。
分かり やすい 具 体 例
例えば ( a、b、 c ) の 3つ の 数 が ( 2、7、9 ) の 組 の とき を 考えてみましょう。 この数 で 式 に当てはめてみると、
【 a+b=c 】 2+7 = 9 【 abc=d 】 d = 2×7×3 = 42
となります。
( 【 abc = d 】 で 使われている 数 は、上にも 書いたとおり 素 因 数 です。a=2、b=7、c=9=3^2なので、ここではc=3となります)
出てきた d = 42をκ>1 の 範囲 ( 例えば κ=2 のとき )で 累 乗 してみると、当たり前ですが d は c より大きくなりますよね。
こんな 感じの 組み合わせは 数 多 く ありますが、もし ( a、b、c ) の 3つ の 数 が ( 1、8、9 ) となればどうでしょう?
同じように 計 算 をしてみると、
【 a+b=c 】1+8 = 9 【 abc=d 】 d = 2×3 = 6
となり、d が cより 小さくなって しまいます。
( 【abc = d 】 で使われている 素 因 数 : a=1、b=8=2^3=2、c=9=3^2=3)
この d = 6 を κ > 1 の 範 囲 で 累 乗 してみるんですけど、このκ、どんな 数 でも良いわけではありません。
もし κ = 2 とかだったら、やっぱり d > c となりますからね。
しかし、κ = 1.2 とした場合だと、d は c より 小さくなるんです。
(κ = 1.2 のとき )6^1.2 = 8.58………
これまでは、パソコン などの 計 算 によって、こういった 「 d が c より 小さくなる 」 み合わせの 数 が 『
κ>1.6』に限ったもので見つかっているということだけが分かっていました。
そんな中で、ABC 予 想 で は
- κ = 2 ( もしくは 2 以上 ) となるような 数 の 組 は存在しない
- 反例のない、ある 実数 が存在する
- κ > 1 となるよう な自然数 の 組は 限られた 個 数 しか存在しない
ということを内容として取り上げていたことから、「 ホントにあるのか……?」 と 数学者 を 唸らせていたんだというのです。
式の証明もそうですが、そもそも 反例 を上げることができないため 「 難しい 」 と言われていたんですね。
望月新一が書いた 論 文 は?
現在、ニュースなどで話題となっている論文については、今後の数学専門誌に記載されるため閲覧することはできません。
しかし過去に提示した論文については、以下のページからPDFファイルとして 確 認 することができます。
宇宙際 タイヒミュラー 理 論 ( Inter-universal Teichmueller Theory ) … 英 語 版 宇 宙 際 タイヒミュラー 理 論 Yahoo
しかもこれはほんの一部で、全体の ページ 数 は 500 を 超えるほど。
住んでいる世界が違うことだけは体験できます(´・ω・`)
まとめ
望月教授が解明したABC予想について、分かりやすい事例が書かれていたので紹介してみました。
問題の数値例などは、以下の引用元を参考としました。
いろいろ端折っている上に、数学的な表し方を省いた部分もあるため、詳細を確認したい場合は以下から確認してみてください。
いちおう全文を載っけておきます。
ABC 予 想 の 具体的な 解 説 ( タップ で 開 く )
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ フレイル 虚 弱 状 態 について
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
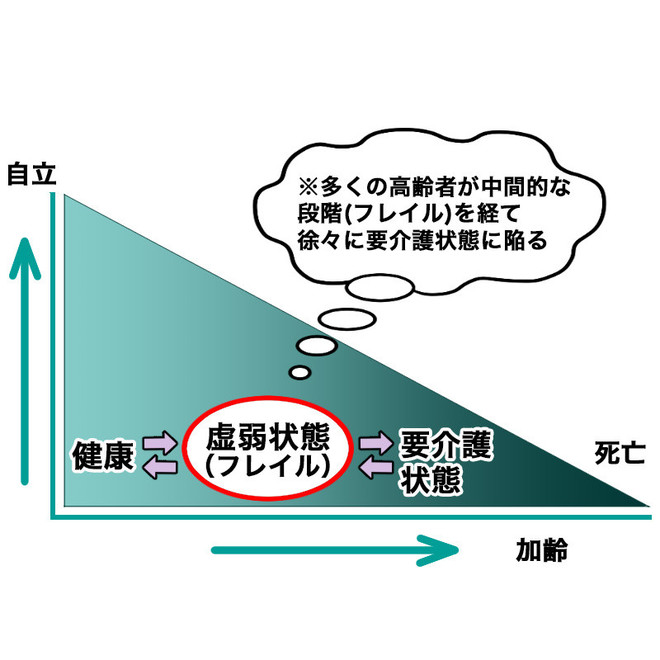
フレイル と は
フレイルは、海外の老年医学の分野で使用されている英語の「Frailty(フレイルティ)」が語源となっています。
「Frailty」を日本語に訳すと「虚弱」や「老衰」、「脆弱」などを意味します。
日本老年医学会は高齢者において起こりやすい「Frailty」に対し、正しく介入すれば戻るという意味があることを
強調したかったため、多くの議論の末、「フレイル」と共通した日本語訳にすることを2014年5月に提唱しました1)。
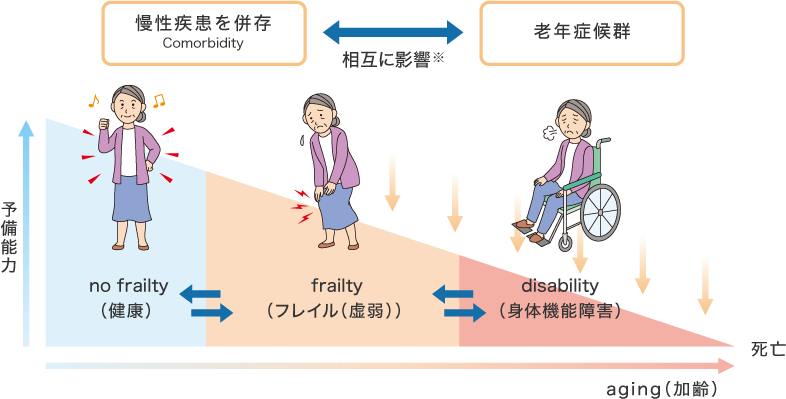
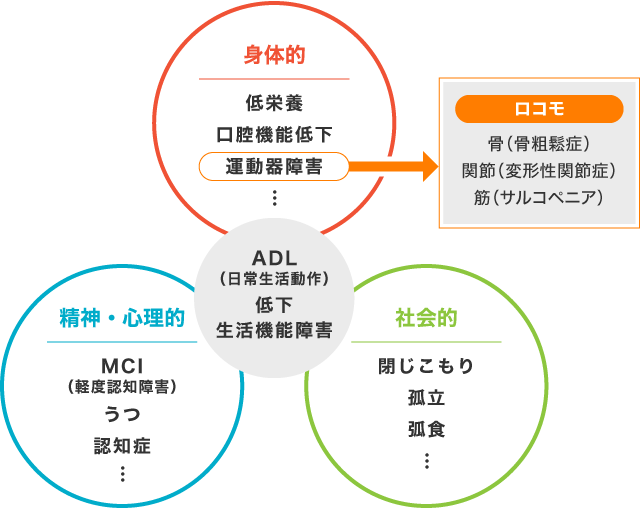
フレイルは、厚生労働省研究班の報告書では「加齢とともに心身の活力(運動機能や認知機能等)が低下し、
複数の慢性疾患の併存などの影響もあり、生活機能が障害され、心身の脆弱性が出現した状態であるが、
一方で適切な介入・支援により、生活機能の維持向上が可能な状態像」2)とされており、健康な状態と日常生活でサポートが
必要な介護状態の中間を意味します。多くの方は、フレイルを経て要介護状態へ進むと考えられていますが、
高齢者においては特にフレイルが発症しやすいことがわかっています。
高齢者が増えている現代社会において、フレイルに早く気付き、正しく介入(治療や予防)することが大切です。
フレイル の 基 準
フレイルの基準には、さまざまなものがありますがFriedが提唱したものが採用されていることが多いです。
Friedの基準には5項目あり、3項目以上該当するとフレイル、1または2項目だけの場合にはフレイルの前段階である
プレフレイルと判断します。
体重減少:意図しない年間4.5kgまたは5%以上の体重減少
- 疲れやすい:何をするのも面倒だと週に3-4日以上感じる
- 歩行速度の低下
- 握力の低下
- 身体活動量の低下

フレイルには、体重減少や筋力低下などの身体的な変化だけでなく、気力の低下などの精神的な変化や社会的なものも含まれます
次に、フレイル状態に至るとどのようなことが起きるか説明します。
フレイル 状態 に 至るとどうなるか
フレイルの状態になると、死亡率の上昇や身体能力の低下が起きます。
また、何らかの病気にかかりやすくなったり、入院するなど、ストレスに弱い状態になっています。
例えば健常な人が風邪をひいても、体の怠さや発熱を自覚するものの数日すれば治ります。
しかし、フレイルの状態になっていると風邪をこじらせて肺炎を発症したり、怠さのために転倒して打撲や骨折をする可能性があります
また、入院すると環境の変化に対応できずに、一時的に自分がどこにいるのかわからなくなったり、
自分の感情をコントロールできなくなることもあります。
転倒による打撲や骨折、病気による入院をきっかけにフレイルから寝たきりになってしまうことがあります。
フレイルの状態に、家族や医療者が早く気付き対応することができれば、フレイルの状態から健常に近い状態へ改善したり、
要介護状態に至る可能性を減らせる可能性があります。
具体的なフレイルへの介入方法に関しては、「フレイルの予防」の項目で説明します。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
2020 04 28
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★










