np -210 ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
過 去 、この 掲 示 板 に 質 問 した 問 題 を お気に入り に 保 存 しておきました
B B S 過 去 ロ グ 【 物 理 の かぎ しつぽ 】 一 覧 表
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
np -210
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
過 去 、この 掲 示 板 に 質 問 した 問 題 を お気に入り に 保 存 しておきました
B B S 過 去 ロ グ 【 物 理 の かぎ しつぽ 】 一 覧 表
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
このページのPDF版 
サイトマップ教えてください 三次方程式 の 解 の 公 式 Jon @ 物理 の かぎ プロジエクト
３ ペ−ジ の なかほどに U^3 + V^3 ＝ -2q U^3 V^3 ＝ -p^3 と 分解方程式 ( ２ 次方程式 )
ξ^2 + 2qξ - p^3 との 関 係 について
この 関 係 は どのようにして 導かれる のでしょうか ? 素 人 に 分かるように やさしく 教えてください ０８−０４−２４
2次方程式 の 解 と 係 数 の 関 係 「
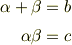となる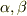 
は の 2次方程式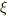 
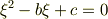
の 解 である． 」 は ご 存 じ ですか?
ご教授 ありがとうございました ． 私 は 不勉強 で この 関 係 を 忘れて おりました． 三次方程式 の 解 の 公式 を 勉
して
いたとき この 関 係 が 理 解 ，納 得 できず いらいらして 欲求不満 になっておりました．
おかげさまで すっきりしました ． 多謝０８−０５−０１
教えてください
ニ−ルス．アベ−ル 更に ガロア により 証明されたという 五次以上の方程式 には 一般代数的解法の公式 がない 】
とあります． ところが，代数学の基本定理には 【 n 次方程式 には 複素数の中に n 個の解を持つ 】 ありますが
これはどういうことなのでしょうか?
解 の 個 数 は 判別 きるが ， その 値 までは 特定できないってことでは？
４次以下の 代数方程式 には ，解 の 公 式 があり，
それによって 解 は 四則演算 と 平方根 や 立方根 の 有限回 の 組み合わせ によって 表されます．
しかし ５次以上 の 代数方程式 では ，解 を 四則演算 と 冪根 の 有限回 の 組み合わせ によって 表す 公式 は
存在しません．
しかし，解 は 存 在 するので ，近似的 に 解 を 求めることは できます．
また， 解を無限級数で表すこともできます． 詳しくは次のページが参考になると思います．
Response ありがとうございました． やはり 天才数学者 の 考える 世 界 なのでしょうか?
RESP ありがとうございました． 五次以上 の 方程式 は 楕 円 関 数 を 使って 解けるようですが
楕 円 関 数 は さらさら分からないので あきらめざるを 得ません． ありがとうございました． 三 輪
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ E 〓 mc2
教えて ください
E 〓 m.c2 の 式 で m の 素 材 について の ことです．
m の 素 材 によって E の エネルギ− は 異なると 思われます．
具体的 に m が 石炭 １ グラム のとき ，この 式 で 計 算 すると
E の エネルキ− は どうなるのでしょうか ?
素 朴 な 質 問 で 恐 縮 します．
三輪次男 さん， 面 白 い 観 点 の お 話 だとおもいます．
「 石炭 １ グラム 」 でも 「 ウラン １ グラム 」 でも 計 算 上 では 同じ エネルギ 値 ですよね．
しかし 物 質 が 地 球 上 の 環 境 で エネルギ 転 換 できるには，
その 物 質 が 「 核 分 裂 」 するか 「 核 融 合 」 を 経 由 する 必 要 があります．
したがって，石炭 や シリコン など手に入り易い物質 では エネルギ 源 とはなりません．
早速 の レス ありがとうございました．
物 質 が地 球 上 の 環 境 で エネルギ− 転 換 できるには，その 物 質 が 「 核 分 裂 」 するか
「 核 融 合 」 を 経 過 する 必要 とのこと．
原子力発電 で 特 別 の 核 燃 料 が 必 要 になるのですね． ０８−０９−０７ 三 輪
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
教 え て ください
物 体 は 高 速 で 移 動 すると 質 量 は 増 加 して ，長 さ は 縮 む といいます．
質 量 ，長 さ を 停 止 状 態 と 高 速 状 態 の 値 をそれぞれ Mo . Mv Lo . Lv と すると
質 量 に 関しては M v ＝ M o / √( 1 - V 2 / C 2 )
長 さ に 関して は L v ＝ L o √ ( 1 - V 2 / C 2 )
とありますが この式 は どのようにして 導かれる のでしょうか．
よろしく お願いします．
多分，このご質問には，多くのサイトで取り上げられているように思います．また，
学ばれる方の勉強方針に依っても，説明する方法も色々有ると思います．
私も数年前から，この掲示版を拝見していますが，基礎的な相対論を学ばれるとするときには；
相対論の考え方， 砂川 重信・著， 岩波書店， ISBN 4-00-007895-5．
を図書館などでご覧の上で，判らない所を質問されると良い様に感じます．
レスポンスありがとうございました．
おすすめの【相対論の考え方，砂川重信著】で検索したらいろんな記事が
ありました．その中で，ロ−レンツ変換に関する記事が参考になりました．
ロ−レンツ変換について勉強してみようと思います．
後期高齢者になった私には一寸重荷ですががんばってみます．
お礼まで ０８−０９−２０ 三 輪
＞後期高齢者になった私には一寸重荷ですががんばってみます．
私も同類です．数年前に，水泳の解析をしたくて流体力学の関連でこちらのサイトをしりました．
流体力学はユックリと進んでいます．通常の物理一般は，この掲示版を拝見していて，
記憶が塊状に回復しました．
物理を解釈する能力は，囲碁のそれと似ていて，時とともに醸造されるようです(笑)．
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
インタ−ネット で 四次方程式 の 解 を 検 索 して 勉 強 しております．
その中の 四次方程式 の 解 法 ．四次方程式 の 解 の 公 式 （４） 式
y^2 + 1/2（B2 + t）］^2 〓 t（y - 1/2t.B1）^2 - 1/4t.B1^2 - B0 + 1/4（B2
+ t）^2 この 剰 余 項 〓 ０ とした
（５）式-1/4t.B1^2 - B0 + 1/4（B2 + t） 〓 0
整 理 した 三次方程式 t^3 + C2.t^2 + C1.t + C0 〓 0 解 を t 〓 t1 ，t2 ，t3 として おりますが
この 三次方程式 の 解 と 四次方程式 の 解 との 関 係 に どのような 意 味 があるのでしょうか ？ 教えてください
2乗 ＝ 2乗 の 形 にむりやり 変 形 させるのに，ひとまず 
を導入して目的の形になる をみつけているだけですね？
たとえば，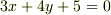 
という 方程式 があったとして，これを 
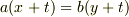の形にしようという目的があったとします．
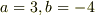はすぐにわかりますから，展開整理すれば 
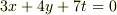最初の式と比べて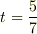 
以上 の 論 理 の 流れが 理 解 できますか？
本 筋 とは 関 係 い 話です． 何 故 ゲタ 記 号 を 等号 代わりに 使われるのですか?
ゲタ記号 〓 は 「 表示不可能文字 」 を表す 写 植 用 記 号 であり，
数学記号 である 等号 ＝ ではありません．このような 文 脈 で 使う文字 ではないと 思います．
下 駄 記 号
こちらにつけておきます
> Yokkunさん の レス への 返 礼 No. 23301 に対して > 数学の証明 はしばしば，トリック を 感じます． > ありがとうございました． ::
> toorisugari no Hiro さん の レスへの 返礼 > 私は，下駄記号 は 知りませんでした． 〓 >
黒 く ，太くて アクセント があると 思ってつかいました．
> おはづかしい次第です．ありがとうございました．
> 以 前，質 問を出したとき返礼ができるような書式であったように思います． > 返信書式 の 画 面 はどうすればよいでしようか？ > 教えてください．
「 返/修/削 」 ボタン を 押して 最 後 にある 欄 に記入するだけです．
[home] [掲示板] [ページの先頭] 最も 初歩的 には ，重力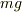 
， 段 差 の 角 での抗力 
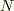， 水平方向の力 
のつりあいを考えればよいと 思います．
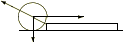
段 差 の 角 を 軸 とする力 の モーメント のつりあいから，車輪中心 と 角 を 結ぶ 半径 の 水平方向 からの 角度を 
として，
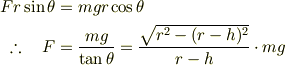
を 得ます．すなわち，
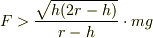
のとき，車 輪 が 段 差 を上がります．下 記 は シミュレーション の 動 画 です．
設 定 は ，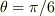 
すなわち， 
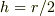で す．
ただし，以上 の 解 析 は，十分 ゆっくりと引いた場合 に上がる 限 界 ということですから，
速 度 をもって 段 差 に 衝 突 する 上がり方 では，また 条 件 が 異なると 思われます．