★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
![]() np - 214
np - 214 ![]()
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
等 号 ( とうごう ) は 「 = 」 の かたち をした 数 学 記 号 である 。 「 イコール 」 と 読む ことが 多 い 。
等 号 の 左 右 が 等 価 であることを 表 し、等 号 で 結ばれた 数 式 を 「 等 式 」 と 呼ぶ。
1557 年 に ウェールズ の 数 学 者 ロバート・レコード に よって 発 明 された。
「 = 」 のことを 等 号 といい,「 = 」 の 両 側 の 表すものが 等しい という 関 係 ( 相 等 関 係 )
を表します。
また,「 >,< 」 のことを 不 等 号 といい,左 辺 と 右 辺 の 値 の 大 小 関 係 を 表します。
等 号 を 使って 表した式 ( 150=90+60 等 ) を 等 式 といいます。
不等号 を 使って 表した式 ( 150<90+70 等 ) を 不 等 式 といいます。
ただし,等 号 や 不 等 号 の 用 語 は 第 3 学年 の 指 導 内 容 で,
等 式 や 不等式 の 用 語 は 指 導 内 容 ではありません。
等号は ,第 1 学年 から 指 導 しますが,下のように 左から 順 に 計 算 して,
その結果 を 示すときに = を 使うといった 意 味 で 扱ってきています 。
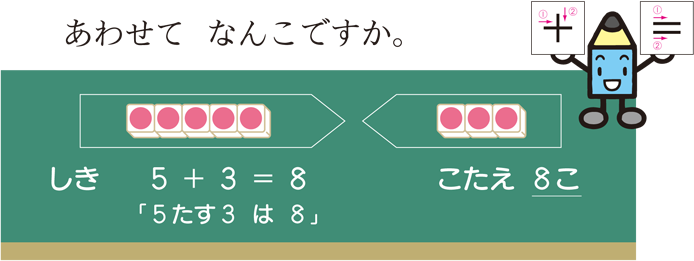
等 号 を 相 等 関 係 を表 す 意 味 で使うのは,第 2 学年 からであり,下のように 指 導 します。

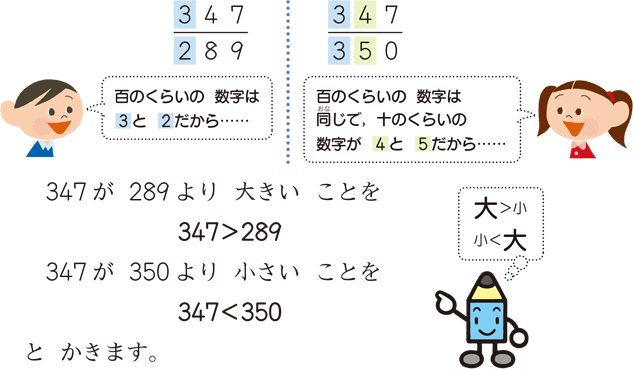
不等号は,下のような 数 の 大 小 をくらべる 場 面 で 導入し,記 号 の 意 味 を 知らせます。
その後,上のような 数 量 の 関 係 を 式 に 表す 場 面 で,等 号 と 同 時 に 扱い,
等 号 や 不等号 を 用いて 数 量 の 関 係 を 正しく 表す ことが できるようにするのです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
私 は 趣 味 で お 遊 び の 数 学 で 時 間 つ ぶ し しております
三次方程式 の 解 の 導 出 する 展 開 式 は A - 4 4~5 ページ あります が
この 展 開 式 の 中 で この 数 学 記 号 〓 ( 等 号 イコール ) が こにうまく 使われているのに 関 心 しました
x3 + a x2 + b x + c = 0 ( 0 1 )
三 次 方 程 式 の 解
X1 = u1 + v1 - a/3 =ω1×(ξ1)1/3+ω1×(ξ2)1/3-a/3 p = b/3 - a2/9
=1×[-q+√(q2+p3)]1/3+1×[-q-√(q2+p3)]1/3-a/3 q = c/2 + a3/27 -a.b/6
=(27c+2a3-9ab)/54
=【-(27c+2a3-9ab)+《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3》1/2】1/3
+【-(27c+2a3-9ab)-《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3 》1/2 】1/3 - a/3
X2 = u2 + v3 - a/3 =ω2×(ξ1)1/3+ω3×(ξ2)1/3 - a/3
=(-1+ i √3)/2 ×【-(27c+2 a3 -9ab)/54+《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3》1/2】1/3
+ (-1-i √3)/2 ×【-(27c+2a3-9ab)-《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3 》1/2 】1/3 - a/3
X3 省 略
三次方程式 の 解 の 導 出 する 展 開 式 を 抜き書き で 並べてみます
変 数 変 換 x = y - ( 1/3 ) a
y3 + 3 p y + 2 q = 0 立方完成 の 式 ( 0 2 ) p = b - ( 1/3 ) a q = c - ( 1/27 ) a3
x の 三次方程式 から y の 三次方程式 に 変 換 されておりますが 中 身 、内 容 は 変わりない 等 値 性
変 数 変 換 y = u + v
展 開 式 を 整 理 すると ( u3 + v3 + 2 q ) + ( u3 .v3 +p3 ) = 0 ( 0 3 )
この 展開式 は 前 の ( ) 内 u3 + v3 + 2 q = 0 後 の () 内 u3 .v3 +p3 = 0
と すれば 0 + 0 = 0 で 方 程 式 は 成 立 する
等 式 の 裏 技 このように 一つ の 方程式 を 二つ の 方程式 に 分 解 する のは 初 め て 見 ました
これは u v の 三次方程式 の 連立方程式 と 表 される
u3 + v3 + 2 q = 0 u3 + v3 = - 2 q
u3 .v3 + p3 = 0 u3 . v3 = - p3
更 に これは 二次方程式 の 解 と 係 数 の 関 係 の 式 と 同 じ 形 です
等 式 の 裏 技 三次方程式 の 連立方程式 が 二次方程式 の 解 と 係 数 の 関 係 式 と 同 じ である
a x2 +b x +c = 0 解 を α β とする と
α+ β = - b / a α 、 β = c / a
従つて 変 数 変 換 y = u + v よ り u3 v3 解 とする 二次方程式 が 導 出 できる
ξ2 - 2 q ξ - p3 = 0
この 二次方程式 の 解 を 逆 戻 しして 行 き 上 記 三次方程式 の 解 に たどり 着 く という 仕 組 み です
蛇 足 三次方程式 の 解 の 公 式 を 導 出 する 展 開 式 の 中 に
u3 , .v3 の 三次方程式 の 解 を 求める くだり がある
三次方程式 の 解 の 公 式 を 知 ら な く ても その 三次方程式 が 容 易 に 因 数 分 解 きれば
解 を 求 め る ことができる
( 三次方程式 ) = ( 一次方程式 ) × ( 二次方程式 )
u3 - a3 = 0 u3 = - a3
u3 - a3 = ( u - a ) ( u2 + a u + a2 )
解 u1 = ω1 a = a u2 = ω2 a = 【 ( - 1 + i √3 ) / 2 】 a u3 = ω3 a = 【 ( - 1 - i √3 ) / 2 】 a
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★