

���w ���� �� �s�v�c �� �W
s - 71
���@�@�@���� �� ���� �� �@�ϕ����� ���@ �ʐ� �� ���� �@�ƂȂ�
�@�@�@�@�@�@�@�@�@�@�@�Q�O�P�X�@�W�@�P�@�@In Put Test�@�@�@�@np - 71 ( �T���� )
�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@���@�@�@�@�@
�@�@�@�@�@�@�@���@�@�@�@�@ �@�@�@�@
�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�~ �� �� �� ���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�~
�� �� ��
�@�@�@�@�@�@�@�@�@�@�@�@L = 2 �� r�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� L d l �@= �� 2 �� r d r �@= �@�� r 2 �@= �@S
���@�@�@�ʐ� �� ���� �� �@�ϕ����� �� �@�̐� �� ���� �@�ƂȂ�
�@�@�@�@�@�@ �@�@  �@�@�@�@�@�@�@�@���@�@�@�@�@
�@�@�@�@�@�@�@�@���@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�~ �� �� ���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�~ �� �� �� ��
�@�@�@�@�@�@�@�@�@�@�@S = �� r 2�@�@�@�@�@�@�@�@�@�@�@�� S d s �@=�@�� �� r 2 d r�@ =�@ (2/3) �� r 3�@�@= �@V
�@�@�@�@�~ �� �� �� �� �� �� ����� �~ �� �� �� �� �ƂȂ�̂� �A �~ �� �� �S ���܂�� �����グ�� �� �~ �� �ƂȂ�
�@�@�@�@�@�@�@�@�@���߂ł��傤���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����ł�
���@�@�@�� �� �\ �� �� �� �� �� ���� �� �� �� �� ���� �~ �� �� �� �� �� �� �� ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �� ���Ƃ� �� �� ���܂����@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �w �� �� �� �w �� �� �� �� �ɂ̂��Ă���܂���
�@�@�@�@�@�@�@�� �� �� ���߂� �� �� �� ������ �܂����A���� �� �� �� �� �� ���� �~ �� �� ������
�@�@�@�@�@�@�@�@���߂� �� �� �� �� �� �� �����t�� �܂���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �t �� �� �� �� �� �� �� �� �� �� ��
�� ������ �Ƃ����B
�@�@�@�]���āA�� �� �� �\�ʐ� �Ƃ��́@�����@����ڂ���@�~���@�́@���ʊ��@�͓��������Ƃ��@���@���@�ł��܂��B
�@�@�@�@�@�@�� �� �\�ʐ� �� �� ���@�@S = 4 �� r 2 �@�́@�� ���� �� ���낢�� ����܂��@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �\ �� �� �@�� �� �� ���@ �@(1)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@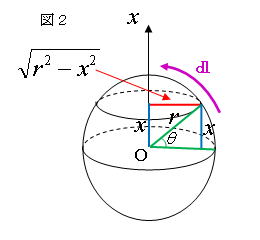
�@�@�@�@�@�@�@�@�\ �� �� �� �� �� �� �� ��� �ɂȂ�悤�ɁA�ϕ����� ��ς��āA�� �� �\ �� �ɉ����� �� �� ����
�@�@�@�@�@�@�@�@�} �ɂ����� �~ �� �� �� �� �\ �� �ɉ������@l�@�����ɐϕ��@������A
�@�@�@�@�@�@�@�@S = 2 �� 0r �� ��@(r2 -x2) d l�@�@���A�@l = r ���@�Ȃ̂ŁA�@x = r sin �Ɓ@�� �u �� ����ƁA�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@S = 4 �� r 2 �� 0 ��/2 ��@( r2 - r2 sin2 ��) r d���@
�@�@�@�@�@�@ �@�@�@�@�@ = 4 �� r 2 �� 0 ��/2 cos�� d���@= 4 ��r2 �k sin���l 0��/2 = �@4 �� r2
�@�@�@�@�@�@�@�@�@�@�@�@�ƂȂ�A�@�� �� �\ �� �� �� �� �� �@�� �� �����Ƃ��ł���
�@�@�@�@�@�@�@�@�@�A�@�@�@�� �� �\ �� �� �@�� �� �� ���@ �@(2)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@
�@
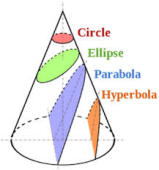
�@�@�@�@�@�@�@�@�@�@�@�@�} �� �悤�ȁ@�R�[���@( �~ �� �� )�@���l����B
�@�@�@�@�@�@�@�@�} �ł́A�P �@�����Ȃ����A���ꂪ �� �� �� �� �� �W ���Ă���悤��
�� �R �l ��
�@�@�@�@�@�@�@�@�� �� �� �Ă���Ɓ@�z �� ���Ă��������B�@ �R�[���@�� ��
�� �́@r�@�Ɓ@�� �����Ƃ��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�l �� �� �� �� ���@�R�[���@�̐����@n �@�Ƃ����
�@�@�@�@�@�@�@�@�P�� �� �R�[�� �� �� �� �� ���@�@Sc�@�Ƃ���ƁA�� �� �́@�@Vc = (1/3) Sc r�@�ƂȂ�
�@�@�@�@�@�@�@�@�@�@�@�@n�@�� �� �R�[�� �� �� �� �� �� �� �a�@���@S�@�Ƃ���Ɓ@�@�@S = n Sc�@
�@�@�@�@�@�@�@�@�@�@�@�� �� �� �� �a �@���@V�@�Ƃ���Ɓ@�@�@V = n Vc = n (1/3) Sc r�@�ł���
�@�@�@�@�@�@�@�@�@�����ŁA�R�[�� �� �� �� �� �� �� �a�@�@S = lim n�����@�� n Sc �� �� �� �\ �� ���@�ƂȂ�
�@�@�@�@�@�@�@�@�@����A�@�R�[�� �� �� �� �� �� �a�@�@V = lim n�����@�� n Vc �� (1/3) S r= �� �� �� ���@�ƂȂ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�]���āA�� �� �\ �� ���@�@S�@ �Ɓ@�� ���@�@V�@�@ �ɂ́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �� ���@V = (1/3) S r�@= �@(4/3)�@�� r3�@�� ���藧�B
�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@����āA�@ �@�@�@�@�@S = 4 �� r2�@�@�@�� ������
�@�@�@�@�@�@�@�@�@�B�@ �@ ���@���@�\ �� �� �@�� �� �� ���@ �@(3)
�@�@�@�@�@�@�@�@�@�@�@�@�� �� �\ �� �� �} �� �����悤�� �� �� �� �� �� �l����B
�@�@�@�@�@�@�@�@�@�@�@������A�� �d �� �� �@���� �� �� �\ �� �� �� �� �� �� ���߂�
�@�@�@�@�@�@�@�@�@�@�@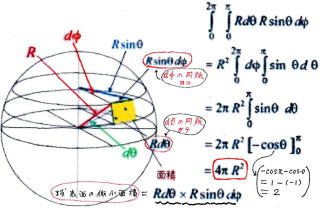
�@�@�@�@�@�@�@�@�@�@�@�@��d�ϕ��A���d�ϕ� �� ���Z����@��w���� �� �� �� ���܂���ł����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�� �������Ȃ̂� �� �� �� �I �� �� �� �� �� ���������̂ł��傤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�������w �� ��� ������ �� ���ł��B
�@�@�@�@�@�@ �@�@�@�@�� �� �� �� �ҁ@8 0�� �ɂȂ��Ă͂��߂� �� �� ���A�� �� �x�@100�@�� �ł�
�@�@�@�@�@
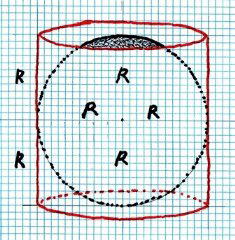
�@�@�@�@�@�@�@�@���@�@�� �� �� �� �����@�~ �� �� �� �� �� �� �� �� �@�� �@�~ �� �� �S �� �� �� �� ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@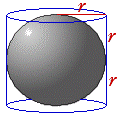
�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� ���@ �@Ss = 4 �� r2�@�@�@�@�@�@�@�@�@�S �� ���@�@St = 6 �� r2
�@�@�@�@�@�@�@�@�@�@�@�@�@Ss =�@(�~�� �̒���)�@�~�@�� �� = 2��r �~ 2 r �@= �@4 �� r 2
�@�@�@�@�@�@�@�@�@�@�@�@�@St =�@Ss + (��ʐ� + ��ʐ�) =�@4��r 2 �{ 2��r 2�@= 6 �� r 2
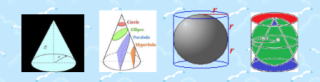
���@�@�@�@�́@�ρ@���@�@�@ �@�~ ���@�B�@���@�B�@�~ ��
�@�@�@�@�@�@�@�@ �@�@�@�@�@�@
�@�@�@�~ �� �� �� �� ���� �� �� �~ �� �ɂ����� �� �� �� �� �W �� �� �� ���܂����@
�@�@�@�@�@�@�@�@�@�@�@�@�� ���@ �� �@�\ �� ���@�́@�� ���@
�@�@�~ ���@�@�@�@�@V = (1/3) S h = (2/3) �� r3�@�@�@�@�@S = ( 1 + ��5 ) �� r2
�@�@ ���@�@�@�@�@�@V = (4/3) �� r3 �@�@�@�@�@�@�@�@�@�@�@ �@S = 4 �� r2
�@�@�~ ���@ �@�@�@ V = 2 �� r3�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ S = 6 �� r2
�@�@�@�@���@�@�@�� �� ��@�@�~ ���@�g�@���@�g�@�~ ���@=�@1 �g�@2 �g�@3
�y (2/3) ��r3 �z�g �y (4/3) ��r3�z�g �y 2 ��r3 �z= (2/3) �g(4/3) �g2= 1 . �Q . 3
�@�@�@�@�@�@�@�@�@�@�@�@���ꂢ�ȁ@�� �� ���@�ł�
�@�@�@�@���@�@�@�� �� �� �\ �� �� �� �� ���@�@�@�@�@�@�� �� ��
�@�@�@�@�@�g�@�� �� �� �� �� �� �� �� ����� �\ �� �� �� �� �� �ƂȂ�@�g
�@�@�@�~ ���@�@d V / d r =�y (2/3) �� r3�@�z= 2 �� r2 ���@S = ( 1 +��5 ) ��r2
�@�@�@�@�@���@�@�@�@dV / d r = �y (4/3) �� r3 �z�M = 4 �� r2 �@= �@S
�@�@�@�~ ���@�@�@�@d V / d r = �y 2 �� r3 �z�M = 6 �� r2 �@=�@ S
�@�@�@�@�@�@�@�@����Ɂ@�g�@�\ �� �� �� �� ���@�� �� �� ����� �� �� �� �� ���@�ƂȂ�@�g
�@�@�@�@�~ ���@�@�@�@�� S d r = ��0 r 2 �� r2 d r = (2/3) ��r3 �@= �@V
�@�@�@�@���@�@�@�@�@�� S d r = ��0 r 4 �� r2 d r = (4/3) �� r3 �@=�@ V
�@�@�@�~ ���@�@�@�@�� S d r = ��0 r 6 �� r2 d r = 2 �� r3 �@=�@ V
�@������@�@�~�� �� �� �� �� �� �� ���@�� �� �� ����������� �� �� �� �� �� ���@�ƂȂ��@
�@�@�@�@�@�@�� Sh d r = �� 0 r�@4 �� r2 d r = (4/3) �� r3 �@= �@V
�@�� ���܂����@�� �� �� �\ �� �� �� �� �� �� �� �� �� �� �� �� �� �����Ƃ��@
�@�@���́@���@���@�́@�� �� �� ���ׂ� �� �߂� ���钆 �� �C �� �� �܂���
�@�@�@�@�@�@�@�� �d�s �v �c�@�ЂƂ�@�x �� �����Ă���܂��@
�@���@ �@ �@�@�@�@�y�@�� �� �� �� �� �� �� �W�@�z
�@�@�@�@�@�@�� �� �� ���@�� �� �� ���@�� ���@������@���@���@�\ �� ���@�� �� ���@�ƂȂ�܂�
�@�@�@�@�@�@�@�@�@�X �� �A�@�� �� �� �� �� ���@ �~ �� �� �� �� ���@ �� �� �� ��
�@�@�@�@�@�� �� �� ���@�� �� ���@�@V = (4/3) �� r3�@�@�@�@dV / d r = 4 �� r2 = �� �� �\ �� ���@�� �� ��
�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�܂� �A�@�� �� �\ �� ���@�� �� ���@�� �� �� ������@�� �� �� ���@�� �� ���@�ɂȂ�܂�
�@�@�@�@�@�@�@�@�� ���@���@�� �� ���@�@�A�@�z�@�@�@���@�\�@�@�� �� �W �ɂ��邱�Ƃ� �� �� ���܂���