np - 115 2017 11 26 U



彌 永 昌 吉 著 ガ ロ ア ニ-ルス アーベル
( 仏 21才 19世紀 ) ( ノルウエーイ 26才 19世紀 )
前 置 き
以 前 日 本 人 の 数 学 者 彌 永 昌 吉 の 資 料 を Net で 拾 い 集 め て い た ら
著 書 ガロア の 時 代 ( 第一部 時 代 編 第二部 数 学 ) を 見 つ け ま し た
さつそく、 取 り 寄 せ ま し た
ガロア は フランス 生 ま れ の 天 才 数 学 者
21 才 の 若 さ で 恋 人 問 題 決 闘 で 倒 れ る
決 闘 前 夜 徹 夜 で 論 文 を 書 い て と い う 原 稿 の 最 後 に は
時 間 が な い 記 してあつた
第二部は本 屋 で 見 た ら 数 式 の 羅 列 でとても歯 が た た な いので Give Up
● 代 数 学 の 基 本 定 理
n 次 方 程 式 に は n 個 の 解 が あ る
an xn + an-1 xn-1 +an-2 x n-2 + ・ ・ + a2 x2 + a1 x + a0 = 0
一 方 、 五 次 以 上 の 方 程 式 に は 一 般 的 代 数 解 は な い と あ る
ただし、 代 数 的 で は な い が 、楕円関数 な ど を 用 い た 根 の 公 式 は
存 在 す る と い う
五 次 方 程 式 の 解 の 公 式 Wipedia
概要[編集]
あ代数学の基本定理によれば、任意の複素数係数方程式は複素数の中に根が存在するが、
しかしながら5次以上の方程式には一般には代数的解法は必ずしも存在しない。
すなわち、一般の五次方程式に対して代数的な根の公式は存在しない。
もう少し詳しく書くと、5次の一般方程式の根を、その式の各項の係数と有理数の、有限回の四則演算及び有限回の根号をとる操作の
組み合わせで表示することはできない。
これはルフィニ、アーベルらによって示され、またガロアによって方程式が代数的に解ける条件が裏付けられている(ガロア理論参照)。
なお、代数的ではないが、楕円関数などを用いた根の公式は存在する。
解の公式[編集]
5次方程式の解を超越的な手続を許して構成する方法としては、
- レベル5のモジュラー方程式の解を利用する方法
- 超幾何級数を利用する方法
の2つが知られている。 前者はエルミートによって、後者はクラインによって証明された
五 次 方 程 式 に は 代 数 解 が な い こ と の 証 明 は ニールス アーベル に よ つ て 証 明 さ れ て い る
さ ら に 、 ガ ロ ア は 群 集 合 の 概 念 を とりいれて 証 明 を 進 化 あ せ た
ガ ロ ア 理 論 と し て 知 ら れ て い る
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
● n 次 方 程 式 の 解
an xn + an-1 xn-1 + an-2 x n-2 + ・ ・ + a2 x2 + a1 x + a0 = 0
◆ 一 次 方 程 式 の 解 a x + b = 0 x = - ( b / a )
◆ 二 次 方 程 式 の 解 a x2 + b x + c = 0 x2 + ( b / a ) x + c / a = 0
平 方 完 成 の 形 に 変 換 し て ( xxx x ) 2 = 常 数 ( x + b/2a ) 2 = - ( c/a ) + ( b/2a) 2

c/a を等式の両辺から引く。すると次のようになる。

この二次方程式は平方完成が適用可能な形となっている。よって、等式の両辺に定数を足し、等式の左辺を平方完成とする。

これを変形する。
 .
.
最後に、右辺の項を変形し公分母を得ることで、次の式を得る。

等式が平方完成された。等式の両辺の平方根を取ることで次の式を得る。

x イコールの形に直すことで二次方程式の解の公式を得る。
◆ 三 次 方 程 式 の 解 x 3 + a x 2 + b x + c = 0
展 開 式 は 省 略 型 に スキツプ し て あ り ま す
y = x + a / 3 x = y - a / 3 と 変 数 変 換 して
y 3 + p y + q ~= 0 と 変 形 する 立 体 完 成 x 2 の 項 が 消 え て い る
さらに 、 y = u + v と 変 数 変 換 し て
u 3 + v 3 = q 連 立 方 程 式 が 得 ら れ る
u 3 × v 3 = - p この 連立方程式 は 二次方程式 の 解 と 係数の関係式 と 同 じ である
従 つ て 、 ξ 2 + 2 q ξ + p 3 = 0 元 の 三 次 方 程 式 の 分 解 方 程 式
ξ は u 3 ・ v 3 な の で
u 3 = - q + √( q 2 + 4 p 3 ) u 1 u 2 u 3
v 3 = - q - √( q 2 + 4 p 3 ) v 1 v 2 v 3
y = u + v y 1 y 2 y 3
◆ 四 次 方 程 式 の 解 x 4 +a x 3 + b x 2 + c x + d = 0
四次方程式 の 解 の 公式 の 導 出 は 二次方程式 、 三次方程式 の 解 の 導 出 を 理 解 しておれば
容 易に 導 出 できる 要するに、変 数 変 換 し て
二次方程式 - A ) ×( 二次方程式 - B ) = 0 の 形 に す る 複 二 次 方 程 式
( 二次方程式 - A ) = 0 、 ( 二次方程式 - B ) = 0 の どちらかが 0 ならば
等 式 は 成 立 する ( 二次方程式 - A ) = 0 の 解 は 2 個 ( 二次方程式 - B ) = 0 の 解 も 2 個
従 つ て 、四次方程式 の 解 は 4 個 得 ら れ る
x
◆ 五 次 方 程 式 の 解
【 五 次 方 程 式 に は 一 般 的 代 数 解 は な い 】
こ れ を 証 明 し た の が アベール ( ノルウエー 19 世 紀 26 才 )
ほ ぼ 同 時 期 に ガ ロ ア ( 仏 19 世 紀 21 才 ) が 群 集 合 置 換 等 の 概 念 を 導 入 し て
さ ら に 、 進 化 させました 有 名 な ガ ロ ア 理 論 で あ る
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
そ の 他、 参 考 資 料
● 日本大百科全書(ニッポニカ)の解説
ガロア理論
フランスの数学者ガロアが提起した方法論で、体(たい)の性質を有限群に関連させて調べる理論。
n次の方程式は重根を重複して数えればn個の複素数解をもつ。これはガウスによって証明された代数学の基本定理である。
二次、三次、四次の方程式は、とくに、係数とn乗根(n=2, 3, 4)を用いて解くことができる。しかるに五次以上の方程式は、
たとえばxn-a=0といった特殊なものを除けば、係数とn乗根だけでは解くことができない。
これが有名なアーベルの定理である。アーベルが19世紀初頭にこれを得たのに引き続いて、
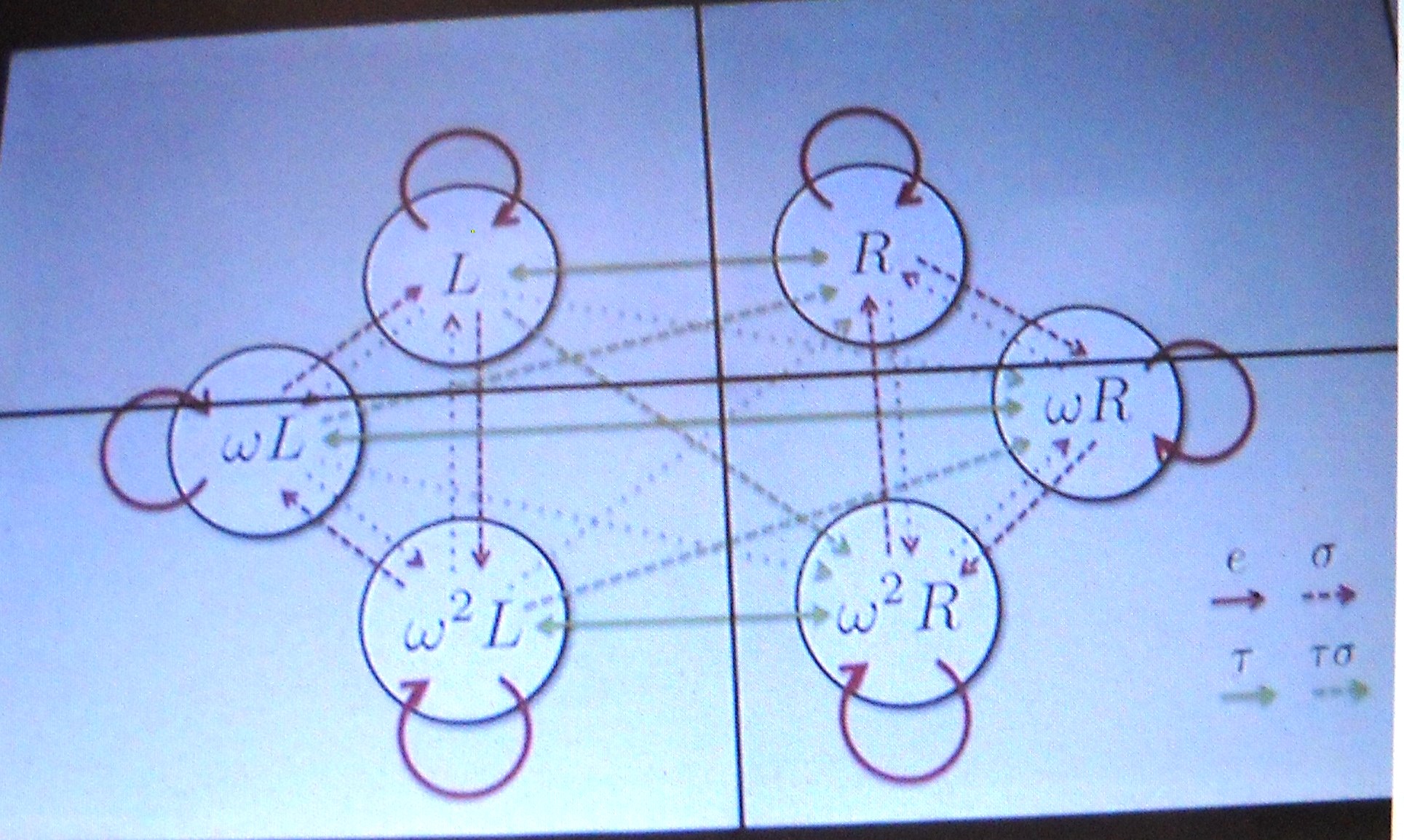
ガロア は、根の間の置換のなす群を研究することによって、べき根によって方程式が解けるかどうかを
群の問題に転化する原理 を確立した。これが ガロアの理論 である。一見、アーベルの定理によって代数学は研究すべき対象を
失ったかに思えたが、実際には古典代数学の幕引きが行われたのであり、以後、群、体などの代数的構造を研究する
新しい代数学が誕生した。
Q でもって 有理数体 を表す。f(x) を有理係数のn次既約多項式とする。方程式f(x)=0の解のすべてをQに添加した体を K とする。
体 K の自己同形の全体 G は群をなし、その位数はnである。この G を K の Q上の ガロア 群 と称する。
G の 部分群 と Kの部分体 とが一定の方法で1対1に対応するというのが ガロアの基本定理 である。
こうして、体の問題が群の問題に転化される。とくにf(x)=0の解が係数とべき根を用いて表されるためには、
G(0) = G, G(n+1) = [G(n),G(n)] ( ここに[G(n),G(n)] は G の 交換子群 である )とするとき、あるnに対してG(n)が
単位元のみからなる群となることが必要十分条件である。このような条件を満たす群を可解群 という。
すなわち、ガロア群 が 可解群 であることが べき根で解ける条件 である。[足立恒雄]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
. ● 間 奏: アーベル の 方程式論 について
歴史的な流れでいうとガロアの少し前にアーベルによる研究がある。ただし、
アーベルの方程式論のことは省略する。
アーベルの扱った問題はガロア理論の前座みたいな役割で取り上げるよりも、ガロア理論、楕円関数論、
数論の交差する問題(「クロネッカーの青春の夢」に至る問題)として扱った方がよいかもしれない。
目次から判断すると、デイヴィッド・A・コックス『ガロワ理論』の第15章「レムニスケート」が多分そのような内容。
ただしそれらが交差するというのはアーベルというよりもガウスの視点で、アーベルは数論的な面の研究はしていないみたい。
ガウスの円周等分方程式論は『数論研究』(1801年)の第7章に置かれその冒頭で楕円関数論の存在がほのめかされている
● 方 程 式 か ら ガ ロ ア 理 論
ガ ロ ア 以 前
ガロアが論文を書くより以前にラグランジュ、ガウス、ルフィニ、アーベルらの研究により、次のような結果が得られていた。
- 2次3次4次の方程式について: 提案されてきた方程式の解法はどれも解の置換の性質と密接に関係している。(ラグランジュ)
- 5次以上の方程式について: 解の置換の性質を調べることにより、5次以上の方程式が一般的にはべき根で解けないことが証明される。
- (ルフィニ、アーベル)
- 円周等分方程式などについて: 解の置換の性質を調べることにより、5次以上でもいくつかのタイプの方程式がべき根で解けることが
- 証明される。 (ガウス、アーベル)
ここからさらに進んで、任意の方程式についての解の置換(=ガロア群)の性質を考察したのがガロアだった、という流れになる。
◆ 対 称 性 ( シンメトリー ) ◆ 間 奏: アーベル の 方 程 式 論 について
◆ 方程式 の 対称性: 2次方程式 の 場 合 ◆ 解 の 置 換 ( ガロア群 )
◆ 3次、4次方程式 の 場 合 ◆ 原始元 の 最小多項式 と 基本定理 の 証 明
◆ 5次以上 の 方程式 の 非 可解性 ( ルフィニ、アーベル ) ◆ 方程式 の 可 解 性
◆ 円周等分 方程式 ( ガウス ) ◆ 追 記: 方程式 の 可解性 の 概 要
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
★ 
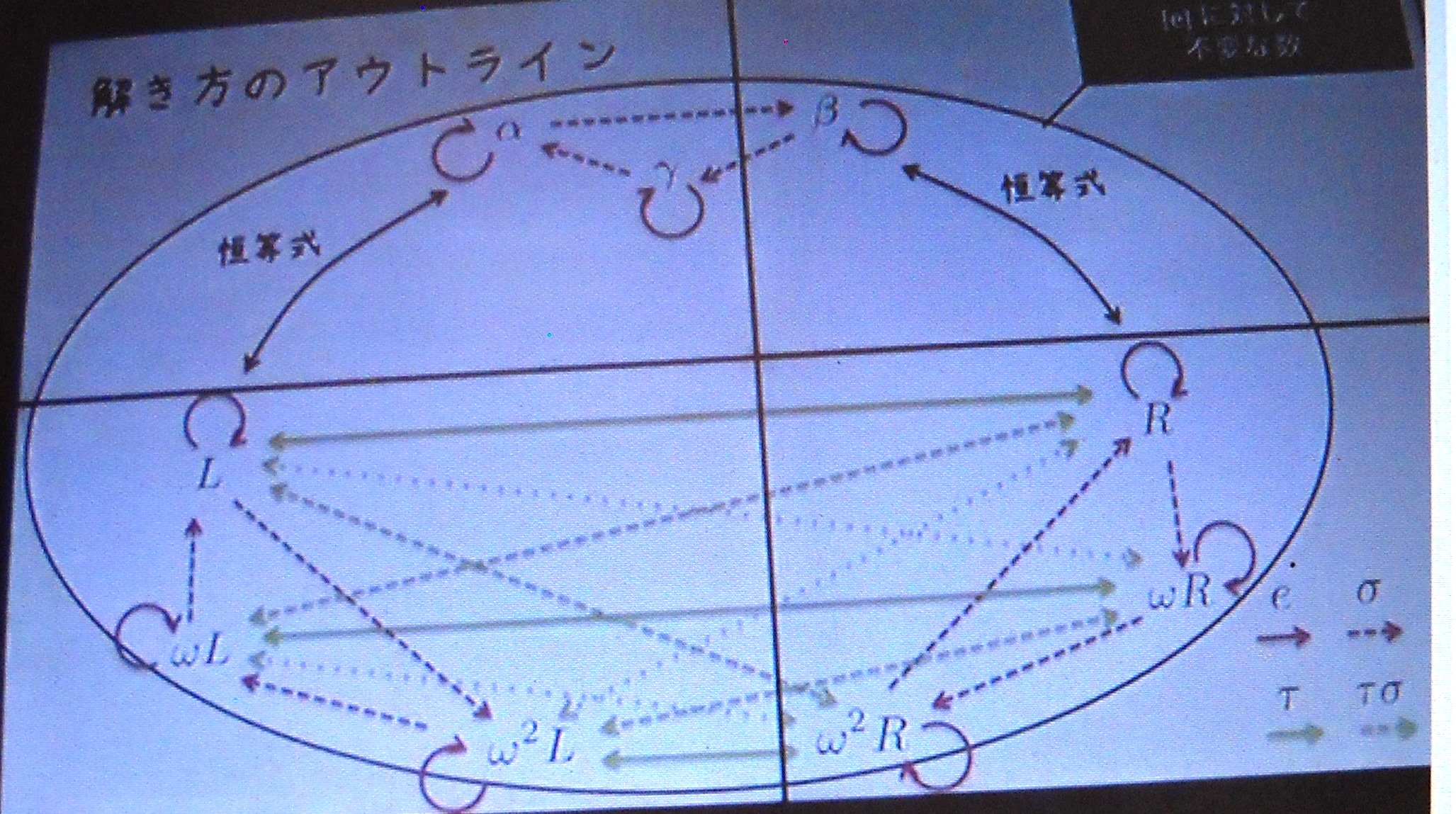
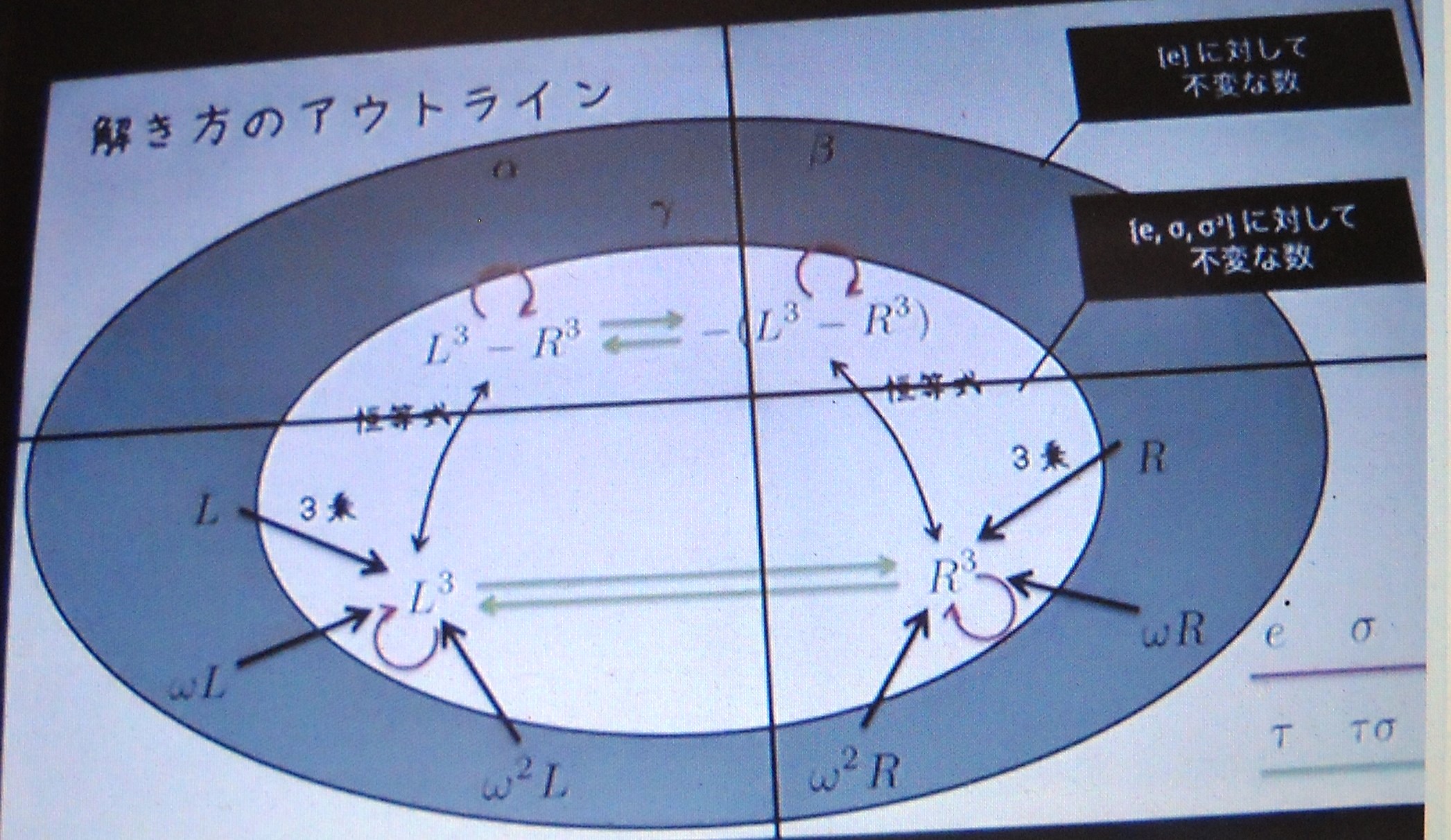
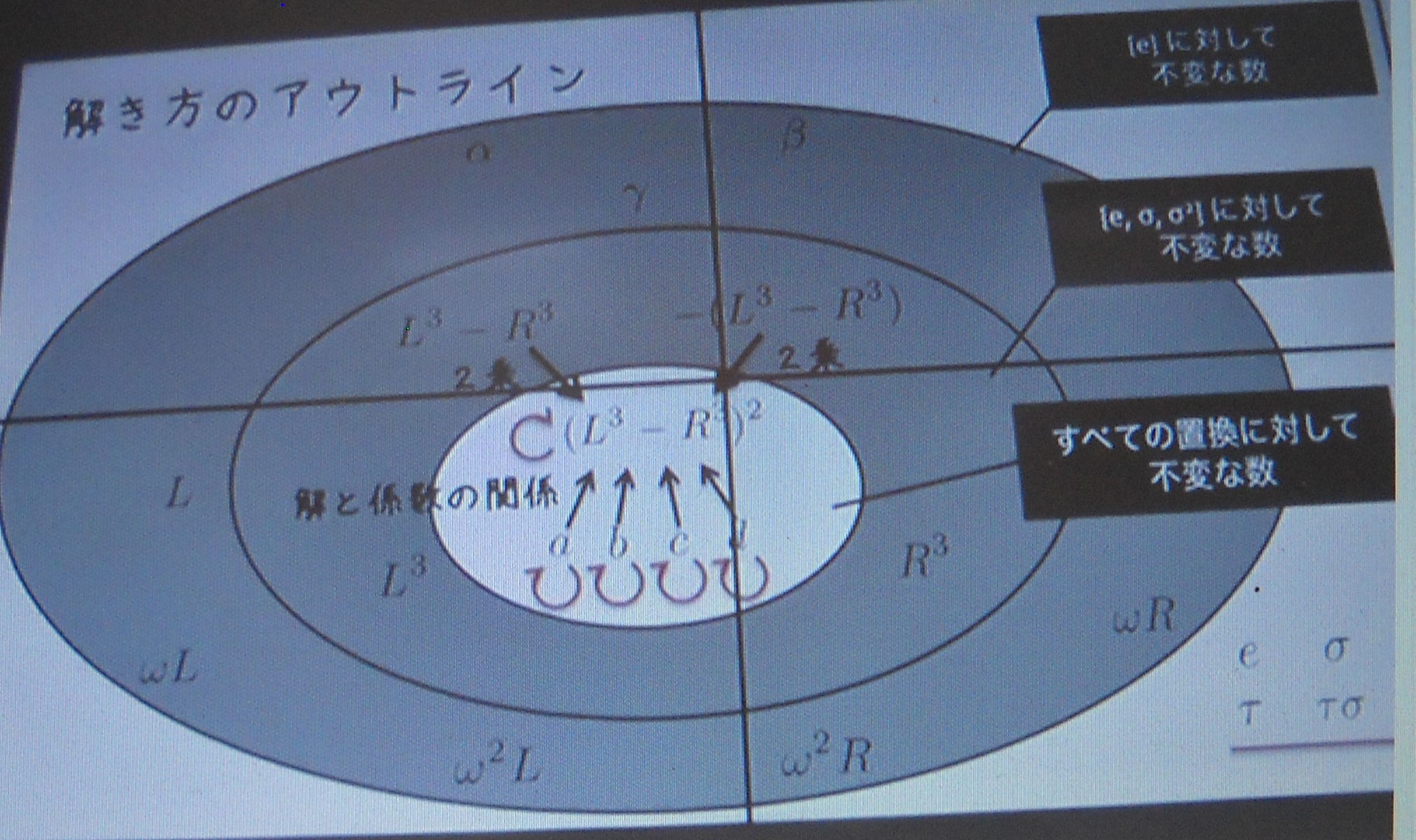
● 五 次 方 程 式 は な ぜ 解 け な い Youtube 動 画 解 説
Youtube で ガ ロ ア 理 論 ( 五 次 方 程 式 に は 代 数 解 は な い こ と の 証 明) の 動 画 解 説 を
見 つ け ま し た
ガ ロ ア 理 論 は 難 し く て 理 解 で き な い が イメージ だ け で も わ か れ ば と 思 い
動 画 解 説 を 静 止 画 像 に 保 存 し て 並 べ て み ま し た
詳 し く は 五 次 方 程 式 は な ぜ 解 け な い を クリツク し て ご 覧 く だ さ い
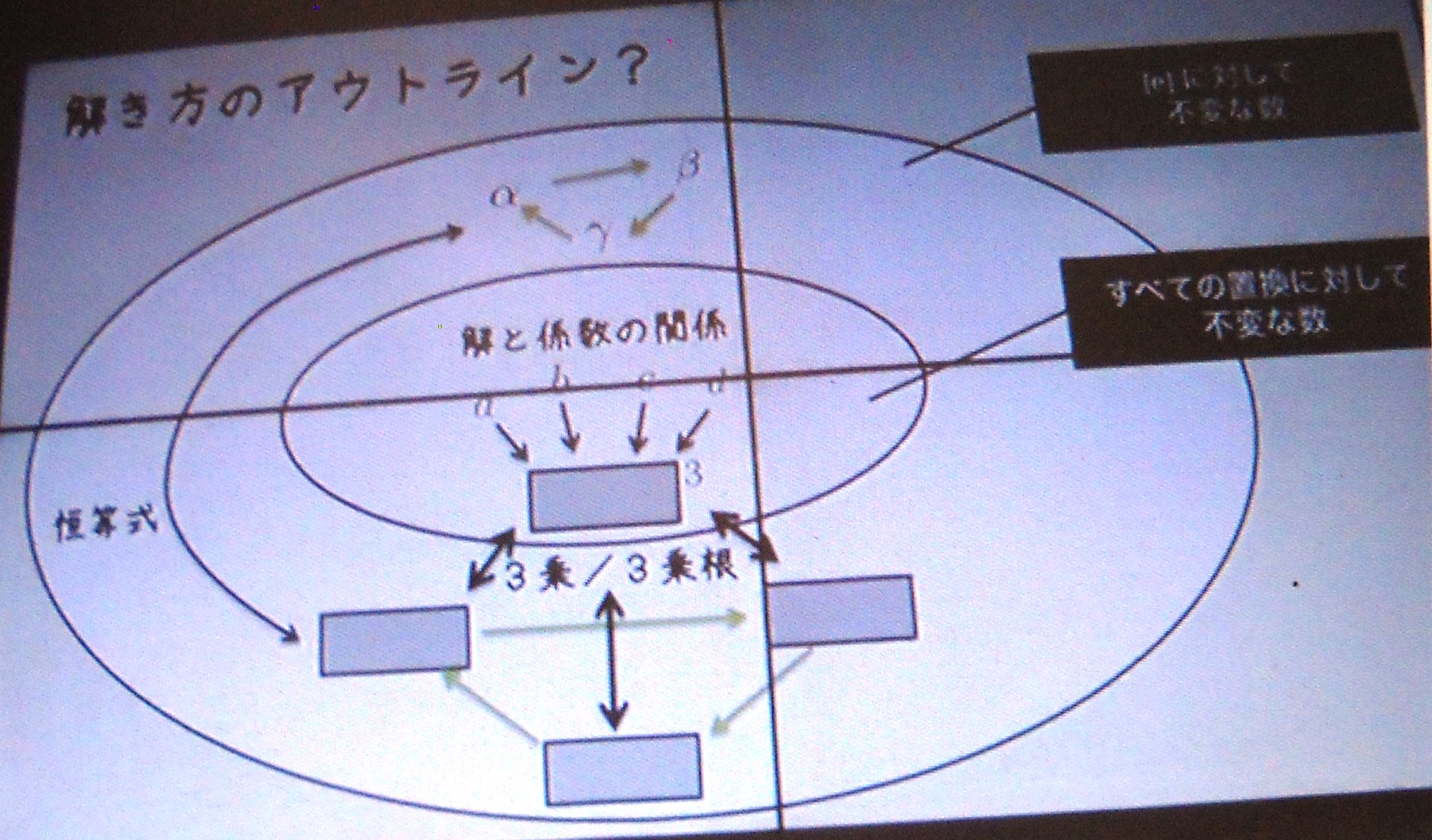
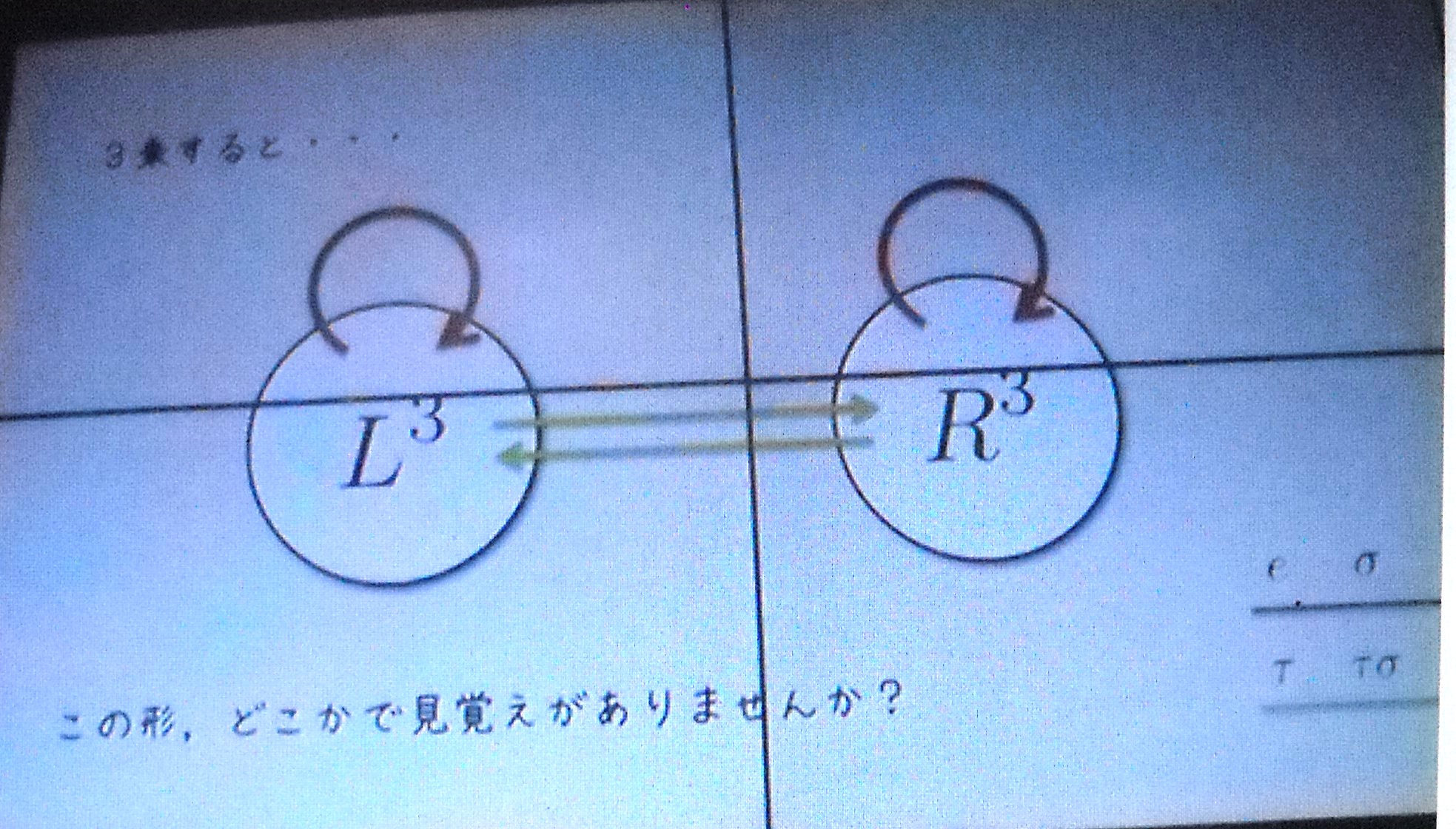
以 下 の 画 像 は ガ ロ ア 理 論 が 理 解 しやすい ように 前 半 に 二次方程式 三次 の 解 の 説 明、
最 後 に 、 五 次 方 程 式 が 解 け な い 証 明 の 説 明 と な つ て い る




二 次 方 程 式 の


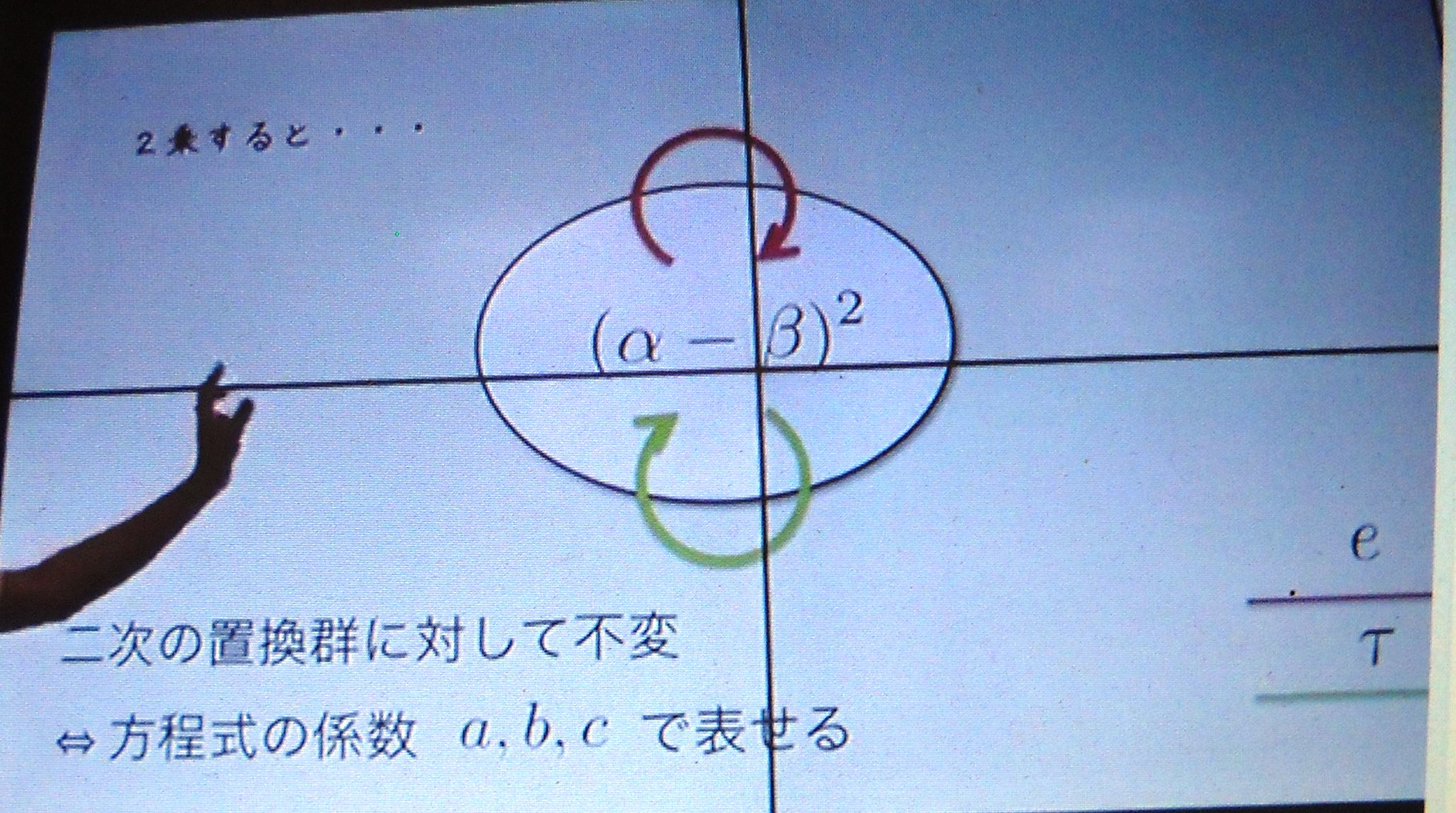



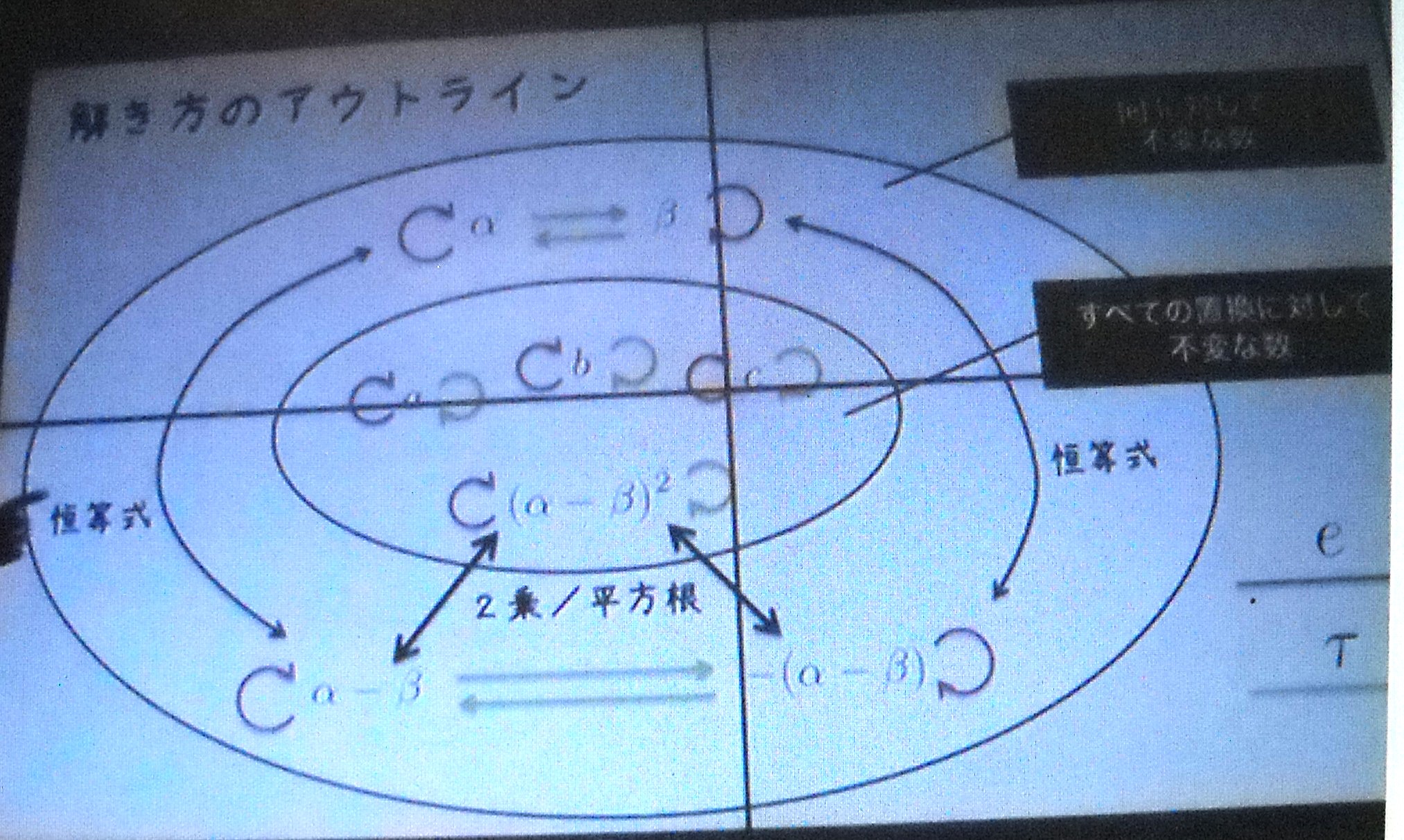
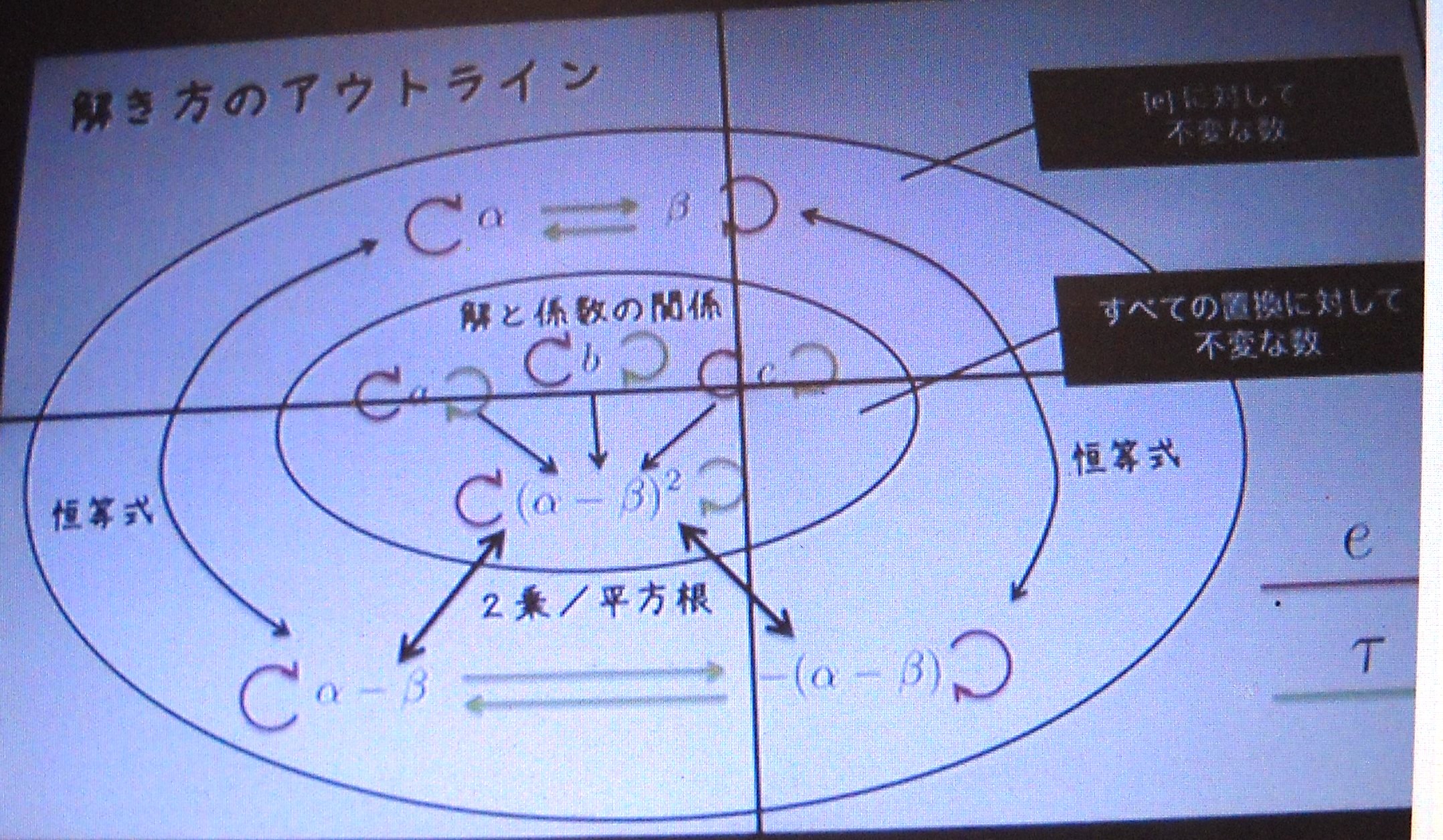


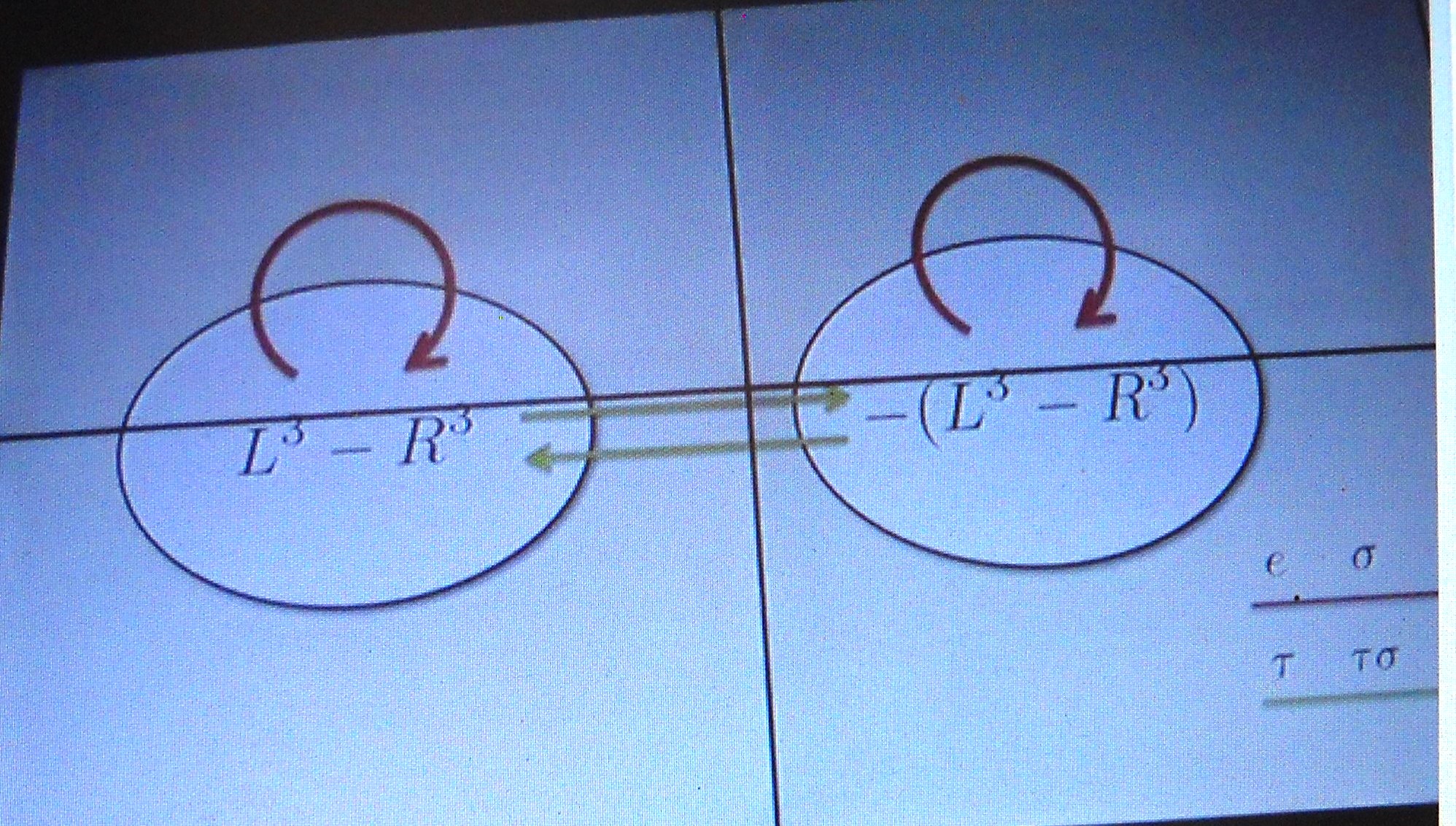
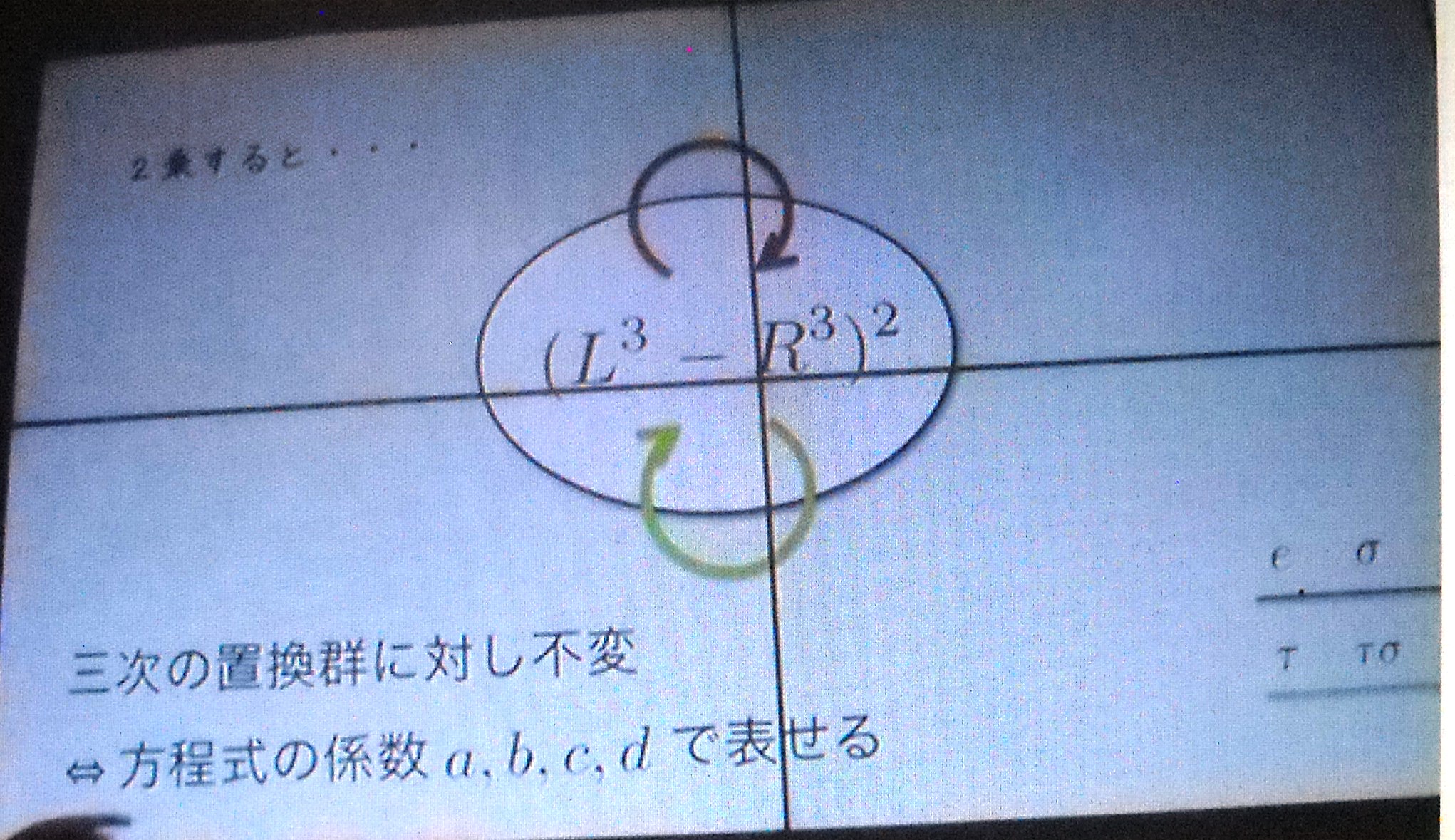
三 次 方 程 式 の 解
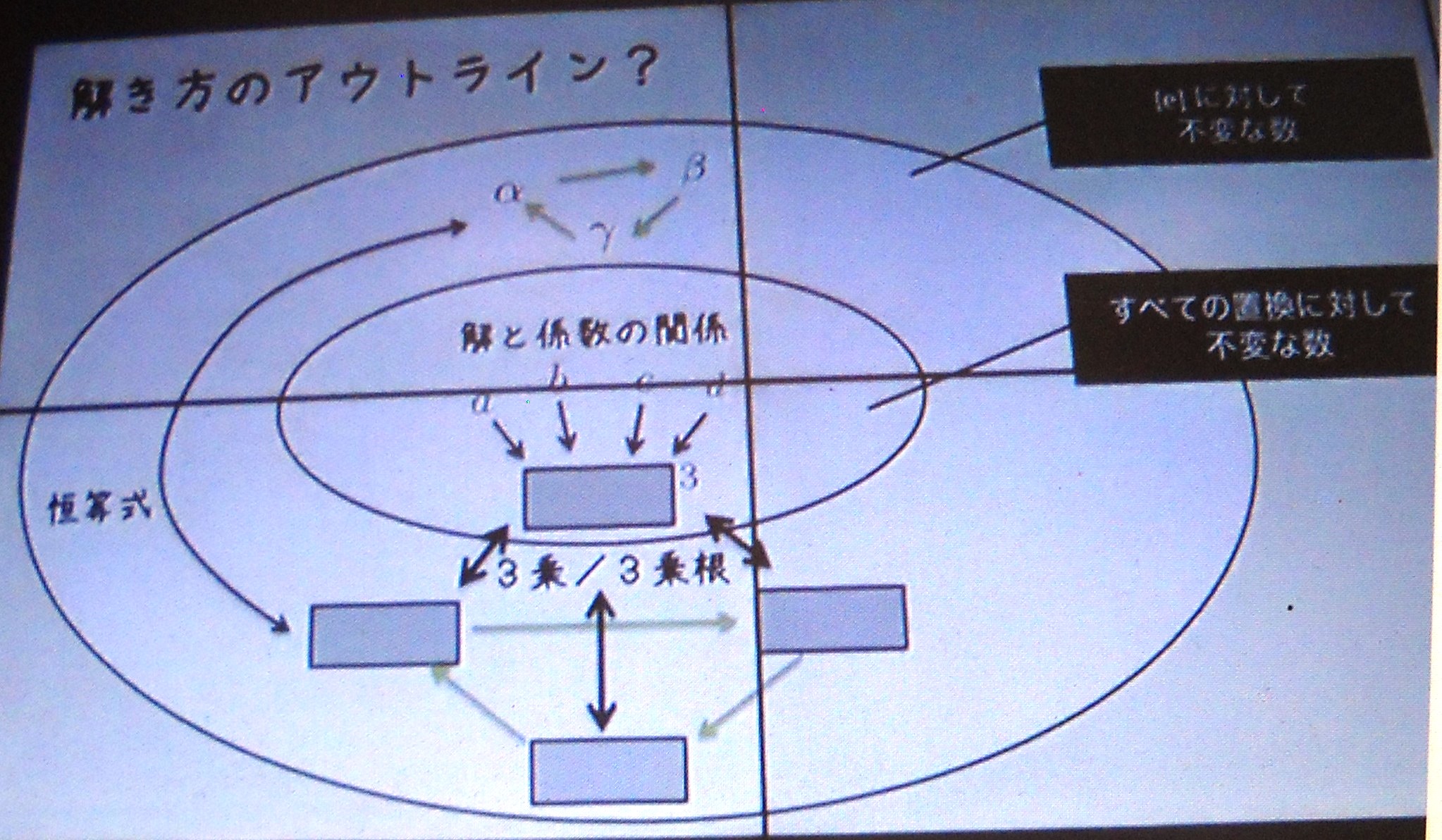

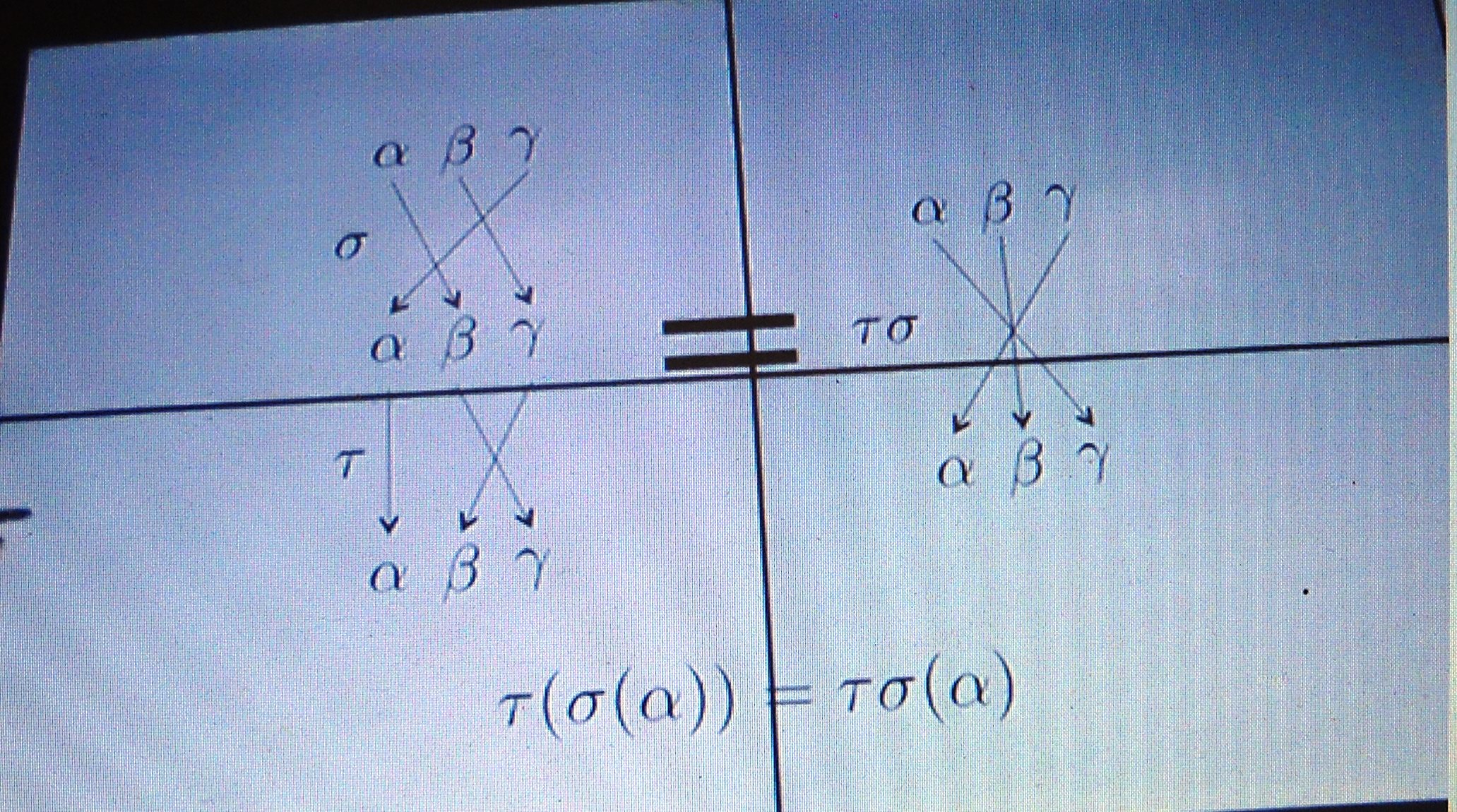




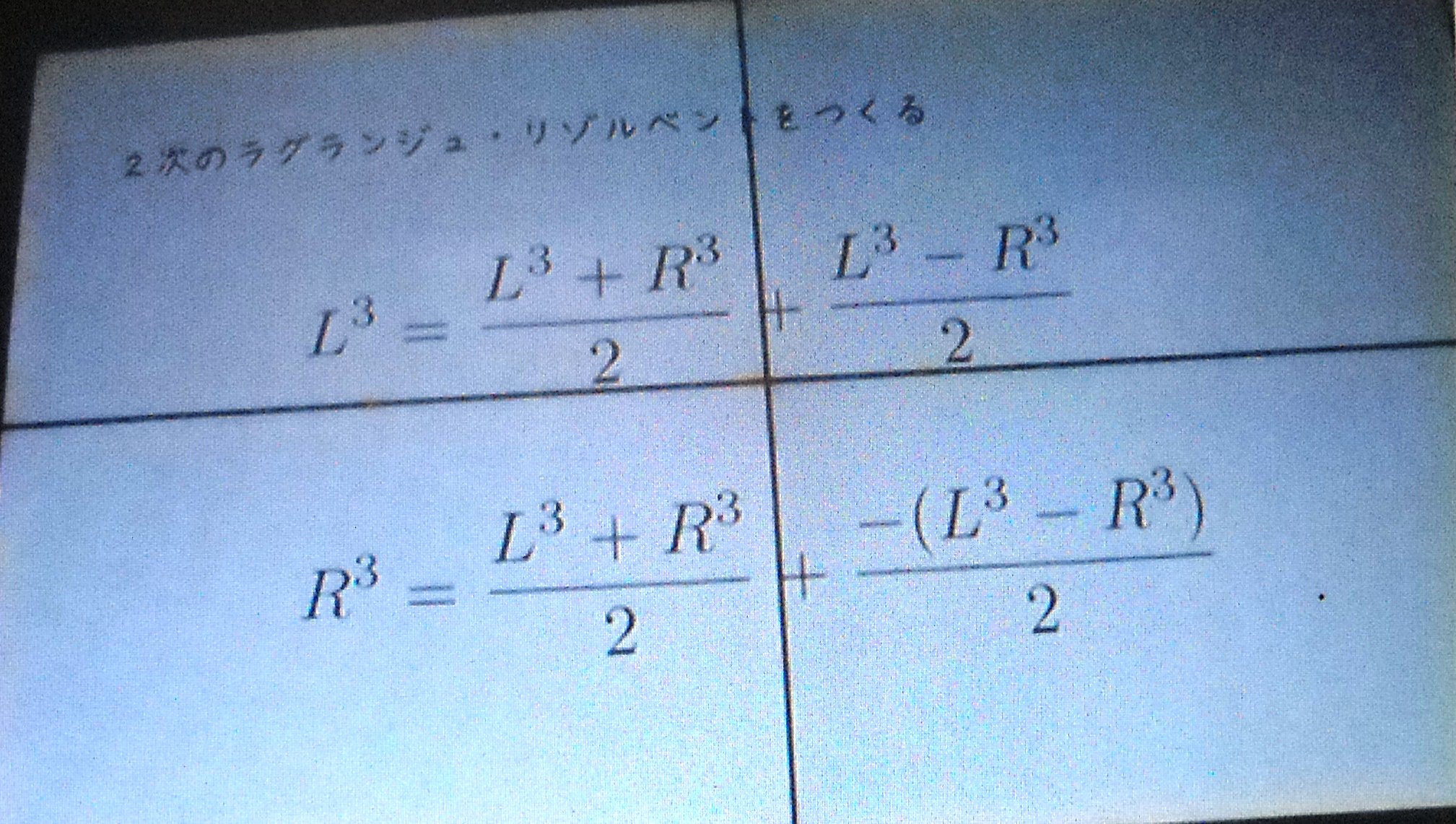


★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
---------------------------------------------------------------------------------------------------------------------------------