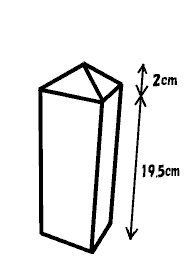
1 リットル 入り の 牛 乳 パック は 空 のときの 体 積 が 1 リットル 1000 cc より ちいさい
下 図 左 断 面 は正方形 で 1 辺 の 長 さ 7 cm
直方体部分 の 体 積 は 7×7×19.5 = 955.5
四角錘 の 体 積 は 7×7×2÷3 = 32.66
よって 全体積 は 約 988.2 cm3
ところが 、新しい 牛 乳 パック を 振ってみると チャプ~ と 音がして 四角錘 まで
満 タン になっていないように 思われます。
しかし、牛 乳 の 量 を 計ってみると ぴったり 1 リットル 1000 cc あります。
摩 訶 不 思 議

牛 乳 の入った パック をよく見ると 少し まるみ を おびている。
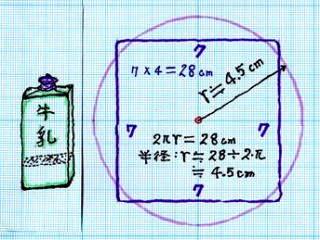
そこで 、周 長 を 計ってみると 7×7 = 28 cm 膨 張 していない。
周 辺 の 長 さ が 同 じでも その形 状 が 異なると 、その 形状 の 面 積 が 異なり ます
ちなみに、 同 じ 周 長 の 正多角形 の 多角形数 を 変えて その 面 積 を 計 算 してみる
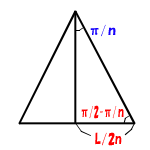
周 長 L の 正 n 角 形 は 【 n 個 の 底 辺 の 長 さ が L / n である 二等辺三角形 】 から 成 る
正 n 角 形 の 面 積 は Sn = 【 ( L / n ) ( L / 2n ) × tan ( π/2 - π/n ) 】 / 2
= L2 / 4n2 × tan ( π/2 - π/n )
三角形 の 高 さ h は h / L / 2n = tan (π/2 - π/n ) h = L / 2n × tan ( π/2 - π/n )
周 長 L = 7 × 4 = 2 8 cm 多角形 数 3 4 6 12 --- ∞ ( 円 )
S3 = (28/3) h / 2 = 37.8 cm2 S4 = 7×7 = 49 cm2 S6 = 【(28/6) h / 2】×6 = 55.8 cm2
S12 = 【 (28/12) h /2 】×12 = 61.7 cm2 S∞ = π r 2 = 3.14 (4.6) 2 = 62.4 cm2
計 算 結 果 を グラフ にします
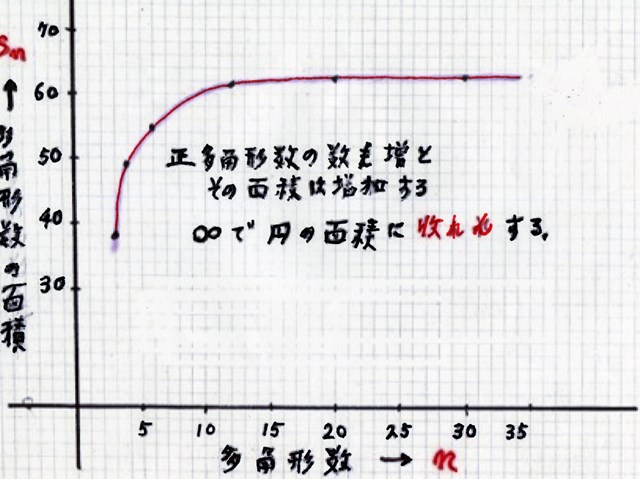
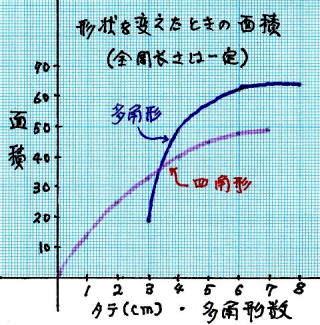

周 長 が 同 じ 長 さ の 正多角形 は 多角形数 を 増すと その 面 積 は 斬 増 します
多角形数 を ∞ すると 円 なります
上 の 例では 周 長 7×4 = 28 cm 円 の 周 長 は 2πr = 28 r = 14/ π
円 の 面 積 S = π r2 = π×(14/π) 2 = 142/π = 62.4 cm 2 で 最 大 となる
★ 参 照 F E M ( Finite Element Method 有 限 要 素 法 ) 流 体 力 学 プログラミング グラフィック作画 等
牛乳 ハック { 弾 性 体 } に 牛乳 を 入れた時 の パック の 変 形 を 数 値 計 算 する
等 周 問 題 ● 等 周 三角形 で 面 積 最 大 は 正三角形 である
● 等 周 多角形 で 面 積 最 大 は 円 である
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
