数 学 の 公 式 面 白 い 関 係
np - 106
数 学 の 公 式 の 中 に 面 白 い 関 係 が あることに 気 づ き ました
長 さの 公 式 を 積 分 すると 面 積 の 公 式 となり 面 積 の 公 式 を 積 分 すると 体 積 の 公 式 となります
さらに 体 積の 公 式 を 微 分 すると 面 積の 公 式 となり 面 積 の 公 式 を 微 分 すると 長 さ の 公 式 となります
具 体 例
円 周 の 長 さ 2 π r 積 分 → 円 の 面 積 π r 2 積分 → 円 錐 の 体 積 (1/3) π r 3
行 き は 積 分 帰 り は 微 分 ↓
円 周 の 長 さ 2 π r 積 分 ← 円 の 面 積 π r 2 積分 ← 円 錐 の 体 積 (1/3) π 3
● 円 周 の 長 さ を 積 分 す る ∫2 π r d r ＝ π r 2 円 の 面 積
● 円 の 面 積 を 積 分 す る ∫π r 2 d r ＝ ( 1 / 3 ) πr 3 円 錐 の 体 積
円 筒 に 内 接 す る 円 錐 と 球 の 関 係
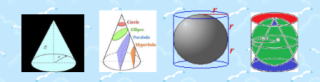
● 体 積 比
円 錐 ： 球 ： 円 筒 1 ： 2 ： 3
V cone ＝ ( 2/3 ) π r 3 V ball ＝ ( 4/3 ) πr 3 V cylinder ＝ 2 π r 3
● 表 面 積 比
円 錐 ： 球 ： 円 筒 ( 1 + √5 ) ： 4 ： 6
1.6 ： 2 ： 3
S cone ＝ ( 1 + √5 ) π r 2 S bal ＝ 4 πr 2 S cylinder ＝ 6 πr 2
自 然 界 の 造 形 に は 不 思 議 な 関 係 が あるものですね
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●