指 数 関 数 y =
e x の
微 分 の 展 開 式 はすぐ 忘れてしまうので
記 録 に 残して おきます。 y =
a x x = log
a y
 ★ ( 解 法 - 1 ) y = e x
△y /△x = y ′= 〔 e ( x + △x ) - e x 〕 / △x (△x → 0)
★ ( 解 法 - 1 ) y = e x
△y /△x = y ′= 〔 e ( x + △x ) - e x 〕 / △x (△x → 0)
= e x 〔 e △x ー 1 〕 / △x
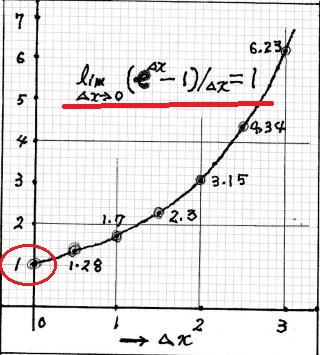
ここで 〔 e △x - 1 〕 / △x ( △x → 0 ) の 極 限 がわかればよい
e および △x に 数 値 を入れて 〔 e △x - 1 〕 / △x を 計算してみる
e △x 〔 e △x - 1 〕 / △x
↓ ↓ ↓
2.71828 3.0 6.23 ← ( 272 3 - 1 ) / 3
2.71828 2.5 4.34
2.71828 2.0 3.15
2.71828 1.5 2.3
2.71828 1.0 1.7
2.71828 0.5 1.28
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
2.71828 0.1 1.05170918075648
2.71828 0.001 1.00050016670838
2.71828 0.00001 1.00000500000696
これより、 〔 e △x - 1 〕 / △x = 1 は容易に理解できます
従って、 △y / △x = dy / dx = y′= e x 〔 e △x - 1 〕 / △x
= e x × 1 = e x
● 追 記 2016 5 20
関 数 f (x) の 微 分 の 解 き 方 には 2 通 り あることを 知 り ました
① 解 析 的 に 解 く 方 法 d (f x) / d x = lim Δx → 0 ( f x + Δx) / Δx
② 数 値 的 に 解 く 方 法 差分法 差 分 方 程 式
d y / d x = f (x) ´ = [ ( f x + Δx ) - f x
】 / Δx
数値解析 における 有限差分法 ( 英: finite-difference methods; FDM )
あるいは単に 差分法 は、微分方程式 を 解くために 微 分 を有限差分近似 ( 差分商 ) で 置き換えて得らるれ
差分方程式 で 近似するという 離 散 化 手 法 を用いる 数値解法 である。18世紀に オイラー が 考案したと言われる
微分方程式 を 解くのに 4 則 加減乗除 数値計算 で求める
例 前 記 e x の 微 分 を 差分法 で 計 算 して グラフ を 描いてみた
4 年 前 に 差 分 法 知らず お 遊 び に やりました
差分法 は 18世紀 に オイラー が 考 案 したという 私 も 面 白 い ことに 気ずき ました にが笑
差分法 は 最 近 シュレヂンガー の 方程式 竹下 淳 著 の 中 で 知りました
★ ( 解 法 - 2 )
y = a x ( a > 0 ) y ′= lim h→0 〔 a x + h - a x 〕 / h = a x lim h→0 〔a h - 1〕 / h
a h - 1 = t とおくと h → 0 の とき a h→ 1 だから t→ 0
また、 a h = 1 + t だから h = log a ( 1+ t )
従って、 y′= a x lim t→0 t / log a ( 1 + t ) = a x lim t→0 1 / ( 1/t) log a (1 + t)
= a x lim t→0 1 / log a (1 + t) 1/ t= a x ( 1 / log a e ) = a x log e a
a = e のとき y = e x y′= ( e x ) ′ = e x log e e = e x
★ ( 解 法 ー 3 ) 簡 便 法
指 数 関 数 と 対 数 関 数 の 関 係 より
y = e x x = log e y
dx / dy = ( log e y ) ′= 1 / y 逆 数 dy / dx = y = e x
やっぱり 微 分 しても 同 じ 式 なんだ
終 わ り
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★