　　　　　　　　　　【　前　置　き　】　　］

　　　　以前、　［末来のコンピューター】　［量子　コンピュ－ター　】　についての記事を新聞で見ました

　　　　　　　　　　　　　　　　　　　　読売新聞　97－3－19　末来のコンピユータ　　あの世のｺﾝﾋﾟﾕーﾀｰ

　　　量子コンピュ－タは計算時間　ゼロ　処理速度　∞　消費電力　ゼロ　とか　夢のような話

　　　理論的には数学的に証明されていると言う。

　　　提案者にはノーベル賞　受賞者の　フｱイマン　もいると言います。

　　　もし、量子コンピタユーターが実現して我々の日常生活　テレビ　カメラ　パソコン　ロボツト　等に

　　　適用されたら　どうなつてしまうのでしょうか。

　　　微の量子の世界　というものは、われ～がおなじみの「この世」の　常　識はまったく通用しません．

　　　理　論の基になっている　「因果律」　そのものが成立せず、統計的な　「量子学」　のみが唯一の

　　　理　論　的　なよりどころ　になります．

　　　　　　　　　　　凡人にはとても理解できそうにありません。

　　　量子論　量子力学　　量　子　世界　を　さまようよつて　みよう　と　思います

　　　　　　　　　　　　　　　　　　イメージ　だけでも　分かれば

　　　　　　　　★　　　量子論　誕生　の　歴史

　

　　　

　　　プランク　(1858 - 1947)　独　　　　アインシュタイン　(1879 - 1965)　独　シュレヂンガー　(1888 - 1961) オーストリア 　

　　　　●　　プランク　の　量子仮説　　　　　（量子論が生まれたキッカケ）

　　　　時は 19 世紀後半、舞台はドイツとフランスの国境、アルザス・ロレーヌ地域のことである。

　　　　この地域は、普仏戦争（1870～1871）でドイツがフランスから手に入れた土地で、

　　　　石炭が多く採掘できることで知られていた。これに目をつけたドイツは、国を挙げてこの付近に製鉄業を興した。

　　　　この製鉄業では、石炭と鉄鉱石を溶鉱炉にいれ、高温で溶かして鉄をつくる。

　　　　この際、溶鉱炉内の温度を正確に知ることが重要なのだが、鉄が溶けるような数千度の温度を測れる温度計など存在しない。

　　　　では、どうしていたのか？

　　　　モノは燃やすと、温度に応じて、さまざまな色の光を出す。そこで、技術者が炉の穴から中を、ひょいとのぞく。

　　　　すると、いまは赤いから 2000 度ぐらい、さらに白っぽくなったから、およそ 4000 度^(注)といったように、溶けた鉄の色の変化で温度を判断した。

　　　いわば、彼らの長年の経験とカンが頼りだったわけだ。

　　　しかし、技術者の間では「経験やカンなどに頼らないで、溶鉱炉内の温度を正確に知る方法はないものか」という声があった。

　　　その声に答える形で多くの物理学者が、この問題に取り組みはじめた。

　　　数多くの実験や測定が繰り返され、ある温度で熱せられモノが、どんな色の光を、どれだけ出すかが、

　　　詳しく調べられた。実験結果も大体まとまったのだが、なぜ、そのような結果になるのか、その原理が、うまく説明できなかった。

　　　それをきちんと理論づけようという試みを、物理学では「黒体放射の問題」と呼んだ。　
　
　　　そして、この研究が、はからずも量子論というミクロの世界の学問を生み出すキッカケになったのだ。

　　　　●　　　アインシュタイン　の　量子仮説　　　　　 ●アインシュタインの光量子仮説

　　　　　　（光電効果）

　　　光のエネルギーは、とびとびの値をとると考える「量子仮説」は、光の波動説をも大きく揺るがした。波のエネルギー（強さ）は波の振幅に比例する。

　　　したがって「光のエネルギーがとびとび」ということは、光の波の振幅も、とびとびの値になることを意味する。これは「波の振幅は連続的な値をとることができる」

　　　とする従来の波の理解の仕方に完全に反するものだった（物理学の世界では、波の種類や大きさなどを「波長」「振幅」「振動数」などの要素で表現する。　　

　　　「波長」は波の１周期の距離である。「振幅」は波の高さを表し波の強さを決定する。「振動数」は１秒間に波が何回うねるかを表す）。

　　　そこに若きアインシュタインが登場する。彼は「光は波ではなく、プランク定数hと振動数νをかけたエネルギーを持つ粒として考えればいい」と主張した。

　　　彼は光の粒を「光量子（こうりょうし）」と呼び、光を粒と考える「光量子仮説」を唱えた。

　　　この考え方に従って、アインシュタインは「光電効果」という現象を説明した。

　　　光電効果そのものを説明する前に、同じ原理である「日焼け」について解説する。

　　　長い間、ストーブの前に座っていても、やけどはするかもしれないが、日焼けはしない。

　　　しかし、直射日光が当たる海辺などでは、すぐに日焼けするのはなぜだろうか？　実はストーブの光は、赤外線で振動数の少ない光であり、

　　　一方、太陽光に含まれる紫外線は、振動数が多い光である。これを光量子仮説の考えで説明すると、ストーブの光のエネルギーは、

　　　振動数νが小さな値なので、エネルギーhνも小さい。これが、肌の分子に当たっても、ほとんど影響を与えない。しかし、太陽の紫外線は、

　　　ストーブの光より振動数νが大きいので、エネルギーhνも大きい。それが肌の分子に、ぶつかって、化学的な変化を引き起こす。

　　　これが日焼けの原理なのである。

　　　光を粒だとするアインシュタインの仮説を使うと、これまでの光の波動説ではわからなかった現象が説明できるようになる。そのひとつが「光電効果」である。

　　　光電効果とは、ある種の金属に振動数の大きな光（たとえば青い光）を当てると、電子が飛び出すという現象のことである。

　　　振動数の小さな光（たとえば赤い光）をいくら長時間当てても、電子は飛び出してこない。

　　　ある一定の振動数以上の光を当てた時のみ、電子が飛び出すのだ。この現象自体は以前から知られていたが、20世紀になってドイツの物理学者レナルトが、　　
　　　
　　　詳しく研究した。

　　　彼の研究結果は、第一に「強い光を当てると、飛び出す電子の数が増える。だが飛び出す電子１個のエネルギーは変わらない」。

　　　第二に「当てる光の振動数を大きくすると、電子は勢いよく飛び出す。つまり、飛び出す電子のエネルギーが大きくなる。ただし飛び出す電子の個数に変化がない」

　　　というものになった。

　　　しかし、この結果は光の波動説では説明できない。光を波と考えると、強い光の波を当てれば飛び出す電子のエネルギーは大きくならなければならないからだ。

　　　なのに、実験では、強い光の波を当てても、電子の数は増えるが、電子のエネルギーは同じなのである。

　　　つまり、強い光であろうが、弱い光であろうが、振動数が同じなら、電子のエネルギーは一定なのである。

　　　また、飛び出す電子のエネルギーを大きくするには、当てる光の振動数を大きくすればいいというのも理解できなかった。

　　　なぜなら、振動数は光の色を決めるもので、　　エネルギーとは関係がないと考えられていたからだ。　

　　　　　（光が粒であることの証拠）

　　　光を波だと考えると「光電効果」を説明できなかった。これに対してアインシュタインは光を粒だとみなして、

　　　光電効果とは、光の粒が金属中の電子にぶつかって、電子をはじき飛ばす現象だと考えた。

　　　そして、この考え方をレナルトの研究にあてはめると、すべてがうまく説明できたのだ。

　　　レナルトの第一の研究結果は「強い光を当てると、飛び出す電子の数が増える。しかし、飛び出す電子１個のエネルギーは変わらない」だった。

　　　この場合の強い光とは、いわば数多くの光の粒が発射されるということに等しい。

　　　光を強くすれば、光の粒の数は増える。すると、光の粒に弾（はじ）かれて、たくさんの電子が飛び出すはずだ。

　　　その際、電子１個のエネルギーが変わらないのは、ぶつかる光の粒のほうがhνという一定のエネルギーしか持っていないからだ（下図参照のこと）。

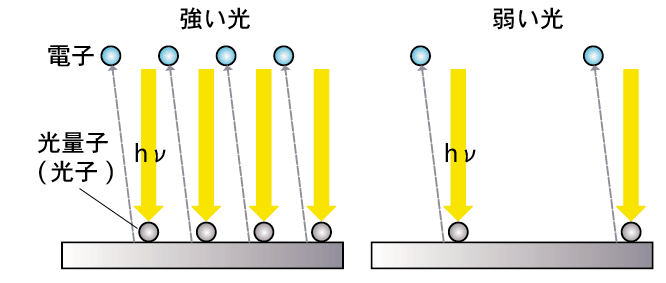
　　　レナルトの第二の研究結果は「当てる光の振動数を多くしても、飛び出す電子の数は変わらない。

　　　しかし、飛び出す電子１個のエネルギーは大きくなる」だった。

　　　この場合、光は単に振動数が多くなっただけで、光の粒を多く発射したことではない。

　　　だから、光の粒に弾かれる電子の数は変わらなくてよいのだ（下図参照のこと）。

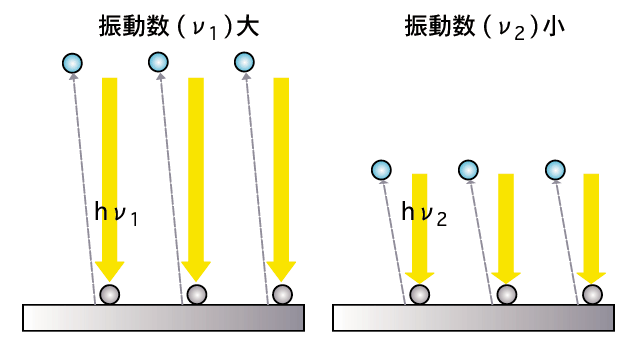
　　　では、飛び出す電子１個のエネルギーは大きくなるのは何故だろう？　「プランクの量子仮説」でふれたが、

　　　光のエネルギーはh（プランク定数）に振動数νをかけたものだった。とすると、光の振動数が多くなれば、それに応じて光の粒１個のエネルギーは増える。

　　　エネルギーの大きな光量子が金属中の電子１個に当たると、飛び出す電子のエネルギーも大きくなるのである。　

　　　　　（コンプトン効果について）

　　　もうひとつ、光を粒だと考えると都合のよい現象に「コンプトン効果」がある。これはアメリカの物理学者コンプトンが、以前から謎とされていたＸ線の散乱波について、

　　　光を粒と考える立場から説明したものだ。

　　　Ｘ線という言葉は、私たちにも、なじみ深いが、その正体は、光よりはるかに振動数が大きい電磁波である。

　　　つまり、光もＸ線も、電磁波であることには変わりなく、ただ振動数が異なるだけなのだ。

　　　物質の原子にＸ線を当てると、当たった後のＸ線は周囲に散乱する。　

　　　散乱後のＸ線の振動数を調べてみると、散乱前の振動数より少なくなっていることがある。

　　　この現象は、光を波だと考える電磁気学の立場からは、説明がつかなかった。

　　　電磁気学の理論によると、散乱前と散乱後のＸ線の振動数は、同じでなければならなかった。

　　　しかし、実験の結果はそうはならない。いったいどうしたものか？

　　　この現象を、光は粒として説明しようとすれば、考え方は光電効果の時と同じようなものになる。

　　　つまり、Ｘ線の粒が原子中の電子にぶつかり、電子を飛ばしながら自分もいろいろな方向に散乱するのだ。

　　　ビリヤードで、テーブル中の的玉（まとだま）に、突き玉（手玉）をぶつけると、当たった後の突き玉のスピードは落ちる。

　　　これは衝突の際に、突き玉のエネルギーの一部が、的玉に奪われてしまうからだ。

　　　逆に的玉は、もらったエネルギーによって動き出す。これと同じようにＸ線の粒も、

　　　原子中の電子にエネルギーを奪われ、そのぶんだけ振動数が少なくなるのだ。（図解雑学　量子論　佐藤勝彦監修　ナツメ社より）

　　　　●　　黒体　と　黒体放射

　　　　

　　　　　　★　　　　シュレーディンガー　方程式　　
　　　　

　　　シュレーディンガー方程式　: Schrödinger equation）とは、物理学の量子力学における基礎方程式である。

　　　シュレーディンガー方程式という名前は、提案者であるオーストリアの物理学者エルヴィン・シュレーディンガーに因む。

　　　1926年にシュレーディンガーは量子力学の基礎理論に関する一連の論文を提出した^[1]。

　　　シュレーディンガー方程式の解は一般的に波動関数と呼ばれる。波動関数はまた状態関数とも呼ばれ、

　　　量子系（電子など量子力学で取り扱う対象）の状態を表す。シュレーディンガー方程式は、ある状況の下で量子系が取り得る量子状態を決定し

　　、また系の量子状態が時間的に変化していくかを記述する。あるいは、波動関数を量子系の状態を表すベクトルの成分と見た場合、

　　　シュレーディンガー方程式は状態ベクトルの時間発展方程式に置き換えられる。

　　　状態ベクトルによる記述は波動関数を用いた場合と異なり物理量の表現によらないため、より一般的である。

　　　シュレーディンガー方程式では、波動関数や状態ベクトルによって表される量子系の状態が時間とともに変化するという見方をする。

　　　状態が時間変化するという考え方はシュレーディンガー描像と呼ばれる

　　　　　　　- ( h 2 / 2m ) / ( d 2 / dx 2 ) Ψ　＋Ｖ Ψ = E Ψ
　

　　　　　　　

　　　

最近、比較的やさしく解説された本　　シュレヂンガー方程式　量子論　量子力学

を見つけたので　量子の世界　に　挑戦してみようとおもいます。　　イメージだけでもわかればと思いまして

　　　　　　　　　　　　　　　　　　　　　

　　　　　　大きさ　比較　　　　　大きな　物質　　から　　極微　の　世界
　　　　　　　　　

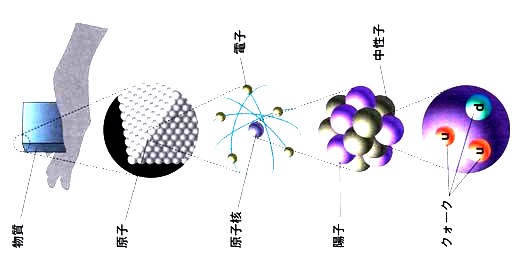
　　　　　　量　子　　　　りょうし　quantum　　　用語解説

　　　　　　　●　　　ブリタニカ国際大百科事典　　小項目事典の解説

　　　　　　　　　　ある物理量が連続値をとらず，ある単位量の整数倍で表わされる不連続値しかとることができない場合，

　　　　　　　　　　この単位量を量子という。 M.プランクが導入したエネルギー量子が最初の例である。

　　　　　　　　　　電気量における電気素量も量子の 1つである。

　　　　　　　　　　本文は出典元の記述の一部を掲載しています。

　　　　　　　●　　　デジタル大辞泉の解説

　　　　　　　　　　　quantum》　一定の最小単位の整数倍という不連続な値をとる物理量、
　　　　　　　　　　
　　　　　　　　　　　その　最小　単位量　プランク　の　量子仮説　で　提　唱　され、エネルギー量子　とよばれたが、

　　　　　　　　　　　のち　アインシュタイン　らにより　普遍的　に　適　用　できることがわかった。　　クォンタム。

　　　　　　　●　　　百科事典　マイペディア　の　解　説

　　　　　　　　　　　ある物理量にそれ以上分割できない最小の単位があり，すべてそれの整数倍として表されるとき，

　　　　　　　　　　この最小単位をその物理量の量子という。　エネルギー量子

　　　　　　　　　　光量子　（電磁波　の　エネルギー量子，光子），　作用量子　（プランク定数）　等がある。

　　　　　　　●　　　世界大百科事典　　　第２版　の　解　説

　　　　　　　　　　　A なる量が，ある単位量の整数倍の値しかとり得ないとき，その単位量を A の量子という。

　　　　　　　　　　　たとえば，光は量子的な構成をもち，振動数が ν ならエネルギーの量子は hν，

　　　　　　　　　　　運動量の量子は h ν/ c である。ここに h はプランクの定数，c は光速度である。

　　　　　　　　　　　プランク定数が作用量子とも呼ばれるのは，量子力学の前身である古典量子論において，

　　　　　　　　　　　量子条件を〈作用量積分が h の整数倍〉とした歴史による。

　　　　　　　　　　　振動数 ν の放射のエネルギーを h ν の整数倍としたのはプランクの放射則の含意をさぐったM.

　　　　　　　　　　　プランク自身であるが (1900) ， h ν を量子と呼んだのは 1909年のプランクから H.A.ローレンツへの手紙が最初である。

　　　　　　　●　　　日本大百科全書　　　(ニッポニカ)　の　解　説

　　　　　　　　　　　振動数　ν　の　光　のエネルギーは h ν （ h はプランク定数）の整数倍で与えられる。

　　　　　　　　　　　この場合のように物理量の値が基礎量の整数倍で与えられる場合その基礎量を量子という。

　　　　　　　　　　　また電磁場に対する光子、中間子場に対する中間子のように、場を量子化したときに現れる粒子を量子ということがある。

　　　　　　　　　　　古典論では一般に物理量が連続的な値をとるものと考えられてきた。

　　　　　　　　　　　量子の発見は古典論から量子力学への移行における決定的な事件であって、

　　　　　　　　　　　量子力学の名称にもこのことが端的に示されている。

　　　　　　　　　　　プランクは、空洞内の放射の分布を正しく与えるためには光を放射し吸収する際の原子の振動子のエネルギーが

　　　　　　　　　　　連続的でなく h ν の整数倍の値に限る必要のあることを示した。

　　　　　　　　　　　またアインシュタインは、光のエネルギーが h ν の整数倍であると考えて、初めて光の吸収によって電子を放出する現象、

　　　　　　　　　　　すなわち光電効果を理解できることを示した。これらはいずれも、エネルギーの量子仮説が、

　　　　　　　　　　　古典論では理解不可能な現象に新しい理解を与えうることを示している。
　　　　
　　　　　　　　　　　ボーアは彼の原子模型のなかで水素原子内電子の定常状態を規定する条件としてボーアの量子条件を与えたが、

　　　　　　　　　　　この条件は電子の作用すなわち運動量をその座標について運動の一周期にわたって積分した量が

　　　　　　　　　　　プランク定数の整数倍であるという形をとっている。［田中　一］