★ マクスウェル の 方 程 式 Wikipedia
● ① div D = ∇. D ( t .x ) = ρ ( t . x ) ガウス の 法 則
こ の 式 の 意 味 ① 電 荷 ( 密 度 ) (ρ ) が 存在したとき、発 散 ( div ) するように 電 場 ( 電束密度 ) ( D ) が生まれる
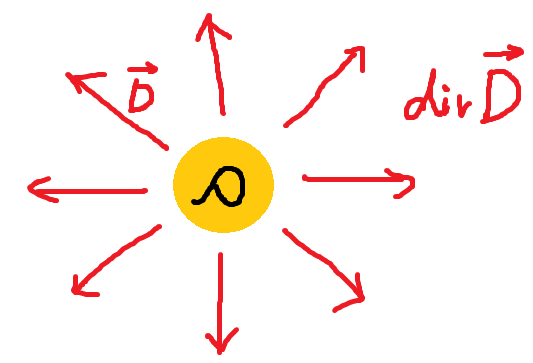
ここで、ρ は、電荷密度(単位は C/m3)。 D は 電束密度 (単位は C/m2)で、
「線形な物質中」では D = ε E の関係がある(E ) は電 場 の 強度、ε は誘電率)。
電場が非常に強くない限り、どんな物質も 「線形」 なものとして扱うことができる。
上の式は、電束 は 電荷 の存在するところで 発生・消滅 し、それ以外のところでは保存されることを意味している。
真空の誘電率 は ε0 と書かれ、次の式で表される。 電荷密度 と 電場 ( マクスウェル . ガウスの式 )
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
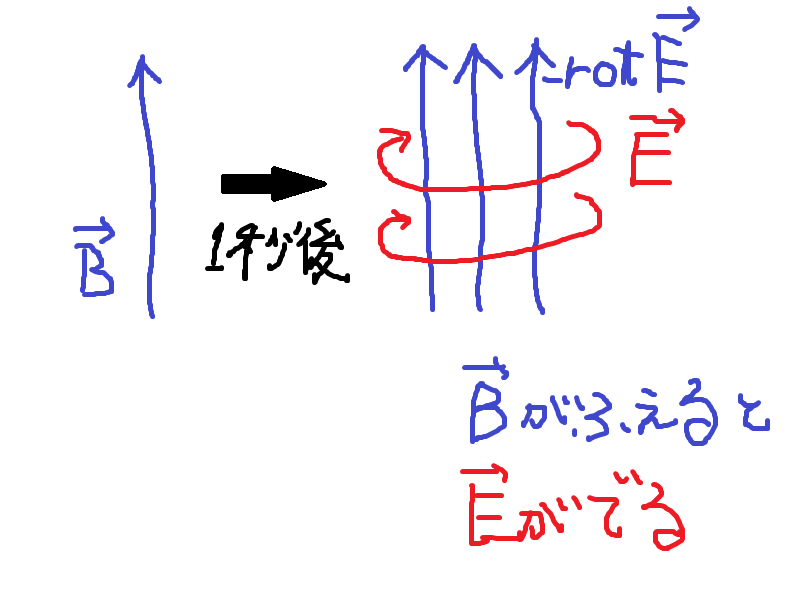
● ② rot E + ∂ B / ∂ t = ∇× E ( t. x ) + ∂ B ( t . x ) / ∂ t = 0
ファラデー の 電 磁 誘 導
こ の 式 の 意 味 ② 磁束密度 (B ) の 時間的 変化 ( ∂ / ∂ t ) が 、右ねじ と 反対方向 (--- rot ) に 電 場(E ) を 生む
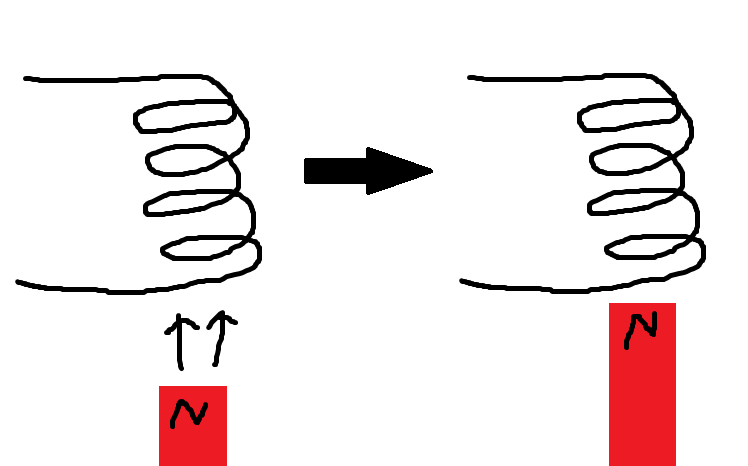
電 磁 誘 導 コイル に 磁 石 を 動 か す と 電 流 が 流 れ る
ちなみに、これは磁石を動かしていないと意味がなくて、コイルの中に磁石をおいても、動いていなかったら、決して電流は流れません
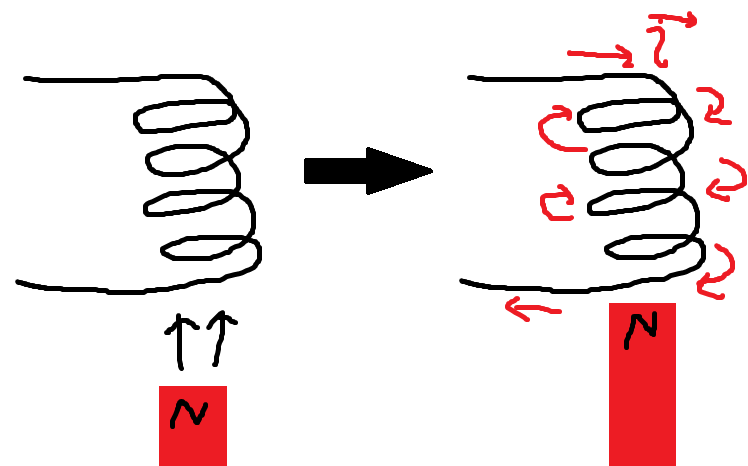
これを式で表すと rot E = - ∂B / ∂t となる訳です
式を 変形すると ∂ B / ∂ t = ー rot E 左辺にあるのは、磁束密度 ( B ) が 時間的変化 ( ∂B / ∂t ) をすることを 示しています
そしてそれに対応するように、右辺 では 右ねじの 反対方向 ( rot ) に 電 場(E ) が 生じる
rotは 右ねじ方向の回転 を表すのでした。これにより生じたE が 、電子があればそれに作用し、電 流 を 流すということです。
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
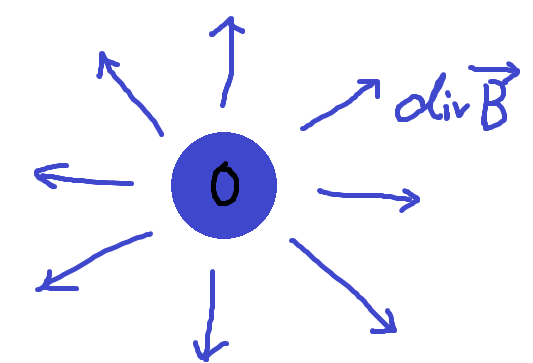
● ③ div B = ∇ ・ B ( t . x ) = 0 磁 場 に 関する ガ ウ ス の 法 則
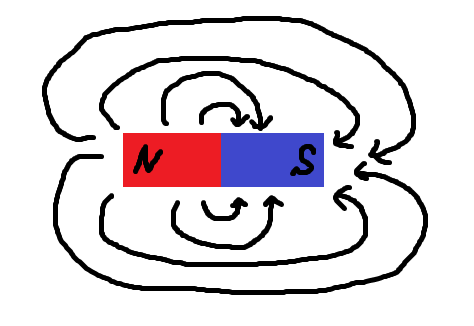
こ の 式 の 意 味 ③ 磁 荷 というものは 存在しない ( 磁 束 密 度(B ) は、発 散 ( div ) し な い ( 0 )

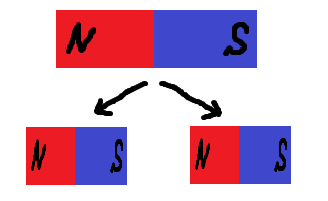
磁 石 は 2つ に 切つても N S ができる N だ け S だ け の 単 極 磁 石 は 存 在 しない
N 極 から 放 出 した 磁 束 は S 極 に 流 入 して + ー ゼ ロ となる 発 散 はない 0
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
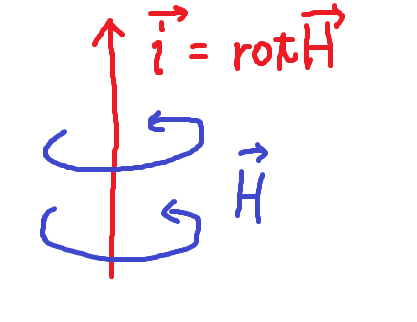
● ④ rot H - ∂ D / ∂ t = ∇ × H ( t . x ) - ∂ D ( t . x ) / ∂ t = i ( t . x )
アンペール . マクスウェル の 方 程 式
こ の 式 の 意 味 ④ 電 流 (i ) と 、電 場 ( 電束密度 ) ( D ) の 時間的変化 ( ∂ / ∂t ) が 、右ねじ の 方 向 (rot ) に 磁 場 ( H ) を 生 む
rot E = - ∂ B / ∂ t は 磁束密度 ( B ) が時間的に変化 ( ∂ /∂ t ) するとき、その 反時計回り ( - rot ) に 電 場 (E ) が 生じる というものでした。
よって rot H = i は、「電 流 ( 密 度 ) ( i ) が 流れたとき、その周りの 時計回り ( rot ) に 磁 場 (H ) が生じる」 という意味です
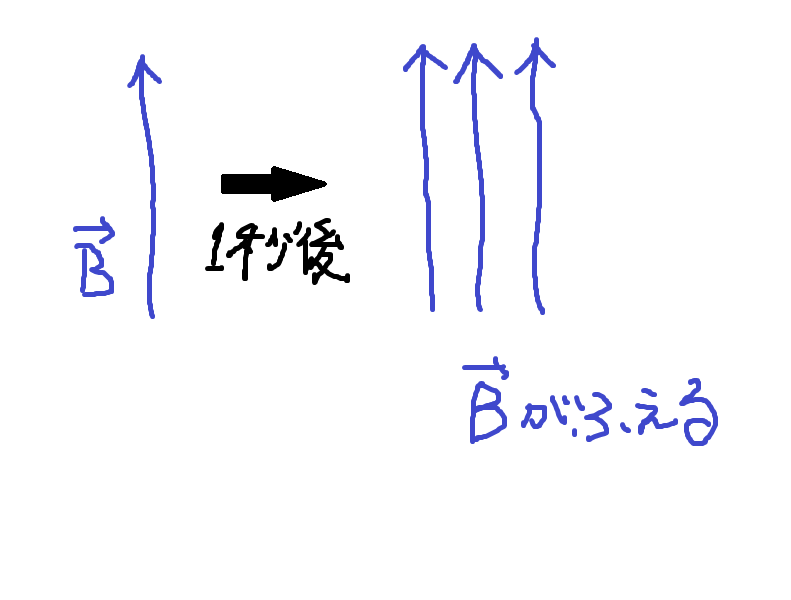
マクスウェル が 追 加 した ∂ D / ∂ t の 部 分 は 、コンデンサー を 考える と 分かりやすい。
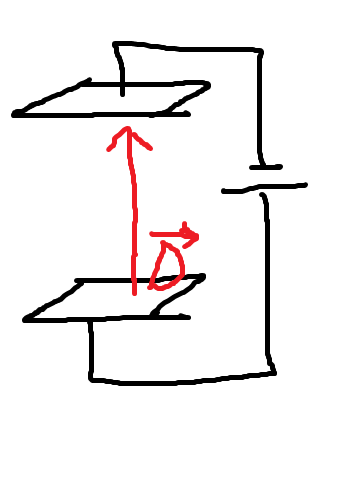
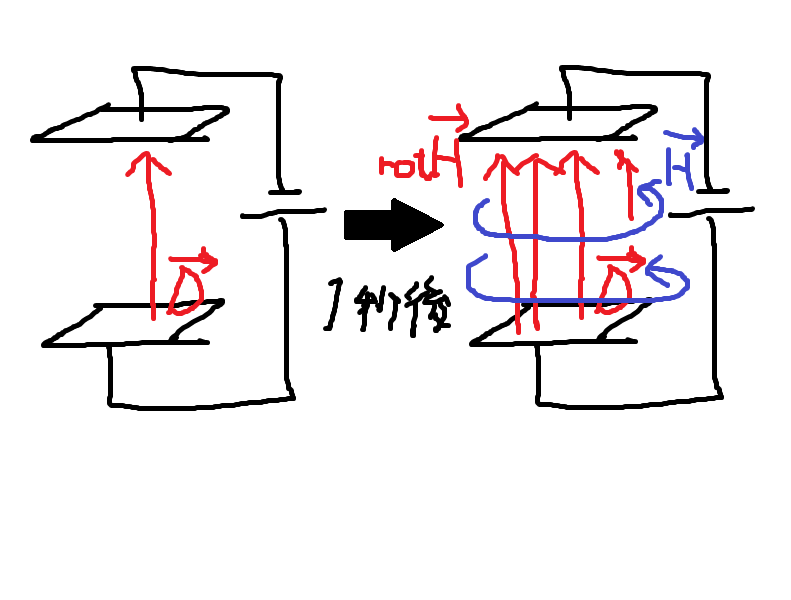
コンデンサー の 極 板 間 は、直 接 つながっていないので、そこを 電 流 ( 密 度 ) が 流れる ことはありません。
しかし電 源 を 調 整 することで、 その間 の 電 場、電 束 密 度D を 変 化 させることはできます。
そして 実 験 によると 、この 電 場 の 時間的変化 は、その 周り の 時計回り の 方 向 に 磁 場 を 生じさせる ことが
分かりました
これは 式 で 言 う と rot H = ∂ D / ∂ となります / ∂t
つまり 直接的 に 電 流 ( 密 度 ) ( ti ) が 流れていなくても、その間 の空 間 の 電 束 密 度 ( D ) の 時間的変化 ( ∂∂t ) は、
まるで 電 流 が 流 て いるかのようにふるまい、
そして 右ねじ の 方 向 に ( rot ) 磁 場 (H ) を 生 じ さ せ る ということです
注 意 してください。
すごく考え深 く、超 ワクワク するところです。 以上が、マクスウェル の 方 程 式 の 解 説 になります
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
★ 『 図 解 』 電 磁 気 学 の 本 質 である マクスウェル の 方 程 式
★ 『 付 録 』
● 発 散
日 本 語 文 例 ストレス を 溌 散 す る
こ の 時 の 発 散 は 減 ら す 減 少 す る 消 す
英 語 文 例 I sometimes need to relieve ( reduce ) stress
.
時 に は ストレス を 発 散 す る こ と が 必 要 だ
科 学 の 世 界 数 学 物 理 学
【 数 学 】 div 【 物 理 の かがしつぽ 】
発 散 Divergence ( div A または ∇ .. A ) ∇ ナ ブ ラ
スカラー場 の 勾 配 を考えたとき,ベクトル微分演算子 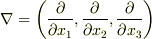 というものを 導 入 しました.
というものを 導 入 しました.
そして,この 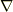 をスカラー関数に作用させたものを 勾 配 (
をスカラー関数に作用させたものを 勾 配 (  )と呼びました.
)と呼びました.
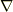 をベクトル関数 と 内 積 を取る形で作用させたものを 発 散 と呼びます.英語で発散を
をベクトル関数 と 内 積 を取る形で作用させたものを 発 散 と呼びます.英語で発散を 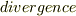 と言うので,
と言うので,
記号 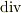 を 使う場合 もあります.
を 使う場合 もあります.
div A - ∇. A = ∂ A1/∂ x1 + ∂ A1/∂ x1 + ∂ A1/∂ x1
ただし 、式 中 ![]() としました
としました
単に 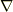 とベクトルの 内 積 になっているだけなので,計算が特に難しいということは無いと思います
とベクトルの 内 積 になっているだけなので,計算が特に難しいということは無いと思います
図 解 説 明 で 発 散 の イメージ を 詠 み 取 り ま す
ここでは,デカルト座標系を考えます.ベクトル場が,点 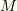 において
において 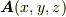 と表現されるとき,
と表現されるとき, 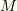 を一つの頂点に,各辺の長さが
を一つの頂点に,各辺の長さが 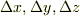 の直方体領域を考えます.
の直方体領域を考えます.
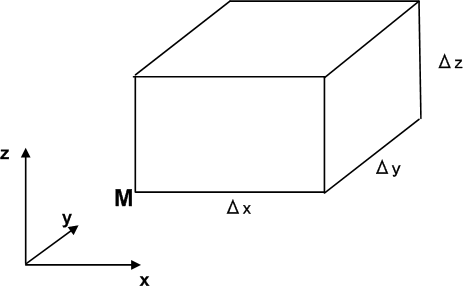
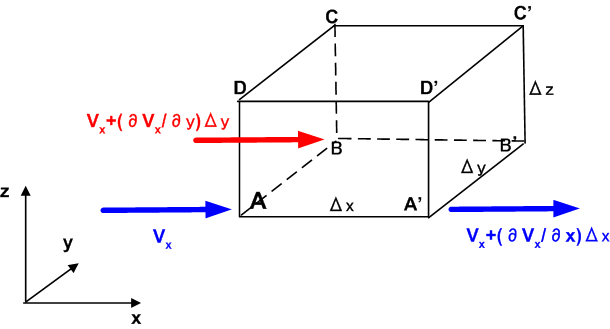
図 ー A 図 ー B

図 ー C 図 ー D
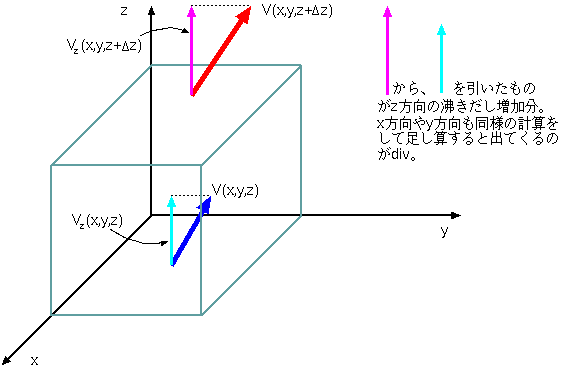
図 ー E
図 ー C . D . E は 別 資 料 からの div の イメージ 図 で す
以 下 図 ー A B に 従 つ て 説 明 し ま す
ベクトル場を,水(非圧縮流体)の流れだと考えると状況がイメージしやすいでしょう.この直方体領域は流れの中に置かれていますから,
絶えず水が流れ込んだり出て行ったりしています
.しかし,水は非圧縮流体だと仮定していますので,普通なら,入ってくる水量と出て行く水量は同じはずです.
ところが,もしこの領域内に"温泉の湧き出し口"のように,絶えず水を噴出している穴が空いているとすれば
込んでしまう排水口のような穴が空いているとしたら,流入する水量の方が多くなりそうです.こうした点を 湧き出し , 吸い込み と呼びます
例として,  軸方向に流入する量と流出する量の差を考えてみます.図のように,頂点
軸方向に流入する量と流出する量の差を考えてみます.図のように,頂点 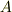 付近に単位面積当たり流入する流体の量は
付近に単位面積当たり流入する流体の量は 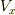 で表わされ,
で表わされ,
頂点 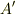 付近では
付近では 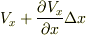 と表わされます.その差は
と表わされます.その差は 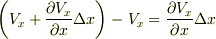 です
です
ここまでは偏微分を定義通りに使っただけです.面倒なのは,正確に表現しようとすると『  方向への変化』されも,
方向への変化』されも,  軸や
軸や  軸に沿って変化することです.つまり,
軸に沿って変化することです.つまり,
頂点  付近で
付近で  方向の流入流は
方向の流入流は 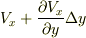 と表現され,さらに
と表現され,さらに  付近ではこの値の
付近ではこの値の  方向への変化を考え,流出流は次式のように表現されることになります.
方向への変化を考え,流出流は次式のように表現されることになります.
(ここで図に全て書き込むとごちゃごちゃしますので描きませんでした.大事なところですので,自分で似たような図でも描いて,しっかり考えてみて下さい.)
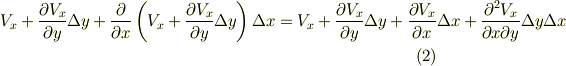
ここで,直方体領域は十分に小さいとすれば,
 方向の流れは "ほぼ一様"だと考えて,二次の変化量(右辺第三項)を無視できます.結局,頂点
方向の流れは "ほぼ一様"だと考えて,二次の変化量(右辺第三項)を無視できます.結局,頂点  付近での流量の差は
付近での流量の差は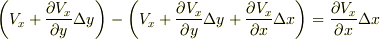 と近似できることになります.これは頂点
と近似できることになります.これは頂点 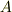 付近の流れと同じになります.
付近の流れと同じになります.  方向に関しても同様に
方向に関しても同様に 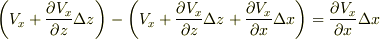 が言えますから,結局,面
が言えますから,結局,面  に流入する流体と,面
に流入する流体と,面 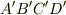 から流出する流体の差は,
から流出する流体の差は,単位面積あたり
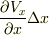 と書いてしまって良いことになります
と書いてしまって良いことになります微小直方体領域で,
 軸方向に『
軸方向に『 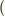 流出した量
流出した量  流入した量
流入した量 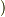 』を,
』を, 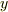 軸方向や
軸方向や  軸方向への二次的な変化を無視すると,単位面積あたり
軸方向への二次的な変化を無視すると,単位面積あたり 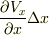 と表わせる
と表わせる ここで  軸方向の流れだけを考えて『
軸方向の流れだけを考えて『 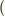 流出した量
流出した量  流入した量
流入した量 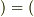 内部で湧き出した量
内部で湧き出した量 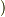 』と考えてしまっては早計です.
』と考えてしまっては早計です.
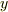 軸方向や
軸方向や  軸方向からの流体の出入りも考慮しなければならないからです.しかし,もし全方向で『
軸方向からの流体の出入りも考慮しなければならないからです.しかし,もし全方向で『 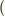 流出した量
流出した量  流入した量
流入した量 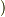 』を考えれば,
』を考えれば,
これは『 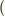 内部で湧き出した量
内部で湧き出した量 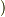 』に等しくなります.
』に等しくなります.
この直方体の  軸方向の断面積(上図の四角形
軸方向の断面積(上図の四角形 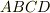 の面積)が
の面積)が 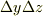 であることに注意すると,
であることに注意すると,  軸方向の流量の差
軸方向の流量の差 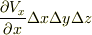 と表わされます.
と表わされます.
同様に, 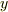 軸方向の流量の差は
軸方向の流量の差は 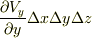 ,
, 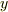 軸方向の流量の差は
軸方向の流量の差は 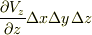 となり,この直方体全体から流出する流量はこれらを足して次式になります.
となり,この直方体全体から流出する流量はこれらを足して次式になります.
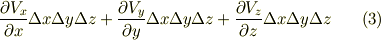
最後に,これを直方体の体積
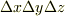 で割れば, 単位体積当たりの 湧き出し量 の表式を得ます.これは,もうお気づきのように div V になっています
で割れば, 単位体積当たりの 湧き出し量 の表式を得ます.これは,もうお気づきのように div V になっています単位体積当たりの 湧き出し は
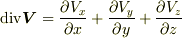 で表わされます.
で表わされます.ベクトル場
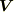 が水の流れ以外のベクトル場であっても,流れの物理的意味は少し異なるかも知れませんが,
が水の流れ以外のベクトル場であっても,流れの物理的意味は少し異なるかも知れませんが,基本的には『単位体積当たりの流れの増減』を表わすのが発散だと考えることができます.
このようなイメージを持っていれば, 電磁気学 で 電場 や 磁場 といった目に見えない場の計算に div が出てきても,慌てることは無いと思います
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
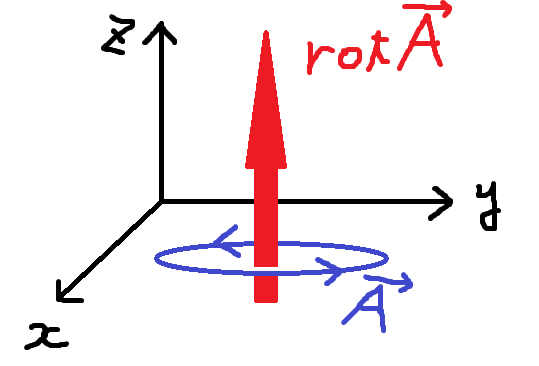
● 回 転 Rotation Curl
【 物 理 学 】 電 磁 気 学 マクスウエル の 方 程 式 に 出 て く る 発 散 div ダイバージェンス
◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆ ◆◆◆◆◆◆◆◆


