Youtube では 小学生 、中学生 、高校生 向けに 数 学 の 問 題 を 動 画 で 説 明 しております
私 が子 供 の 頃 ならった 算 数 数 学 の 教え方 より かなり 工 夫 されております
【 例 】 一 次 、二 次 、三 次 方 程 式 の 解 メ モ を とって 載 せ て みました
方 程 式 f ( x ) = x n + a 1 x n-1 + a 2 x n-2 ・ ・ ・ + a n = 0
★ n = 1 f ( x ) = x + a = 0
x = a
★ n = 2 f ( x ) = x 2 + a x + b = 0
( x + a / 2 ) 2 + b ー a 2 / 4 = 0
( x + a / 2 ) 2 = ( a 2 - 4 b ) / 4
平 方 完 成 ( //// ) 2 = 定 数 の 形
x + a / 2 = ± ( √ ( a 2 - 4 b ) ) / 2 x = ( - a ± √ ( a 2 - 4 b ) ) / 2
★ n = 3 f ( x ) = x 3 + a x 2 + b x + c = 0
( x + a / 3 ) 3 = x 3 + 3 ( a / 3 ) x 2 + 3 ( a / 3 ) 2 x + ( a / 3 ) 3
f ( x ) = ( x + a / 3 ) 3 + ( b - a 2 / 3 ) x + ( c - a 3 / 27 )
( x + a / 3 ) = x ´ ( b - a / 3 ) = p ( c - a 3 / 27 ) = q すると
f ( x ) = x ´3 + p x ´ + q 二 次 の 項 がない 立 体 完 成 という
公式 A x 3+y 3+z 3 - 3 x y z = ( x + y + z ) ( x + w y + w 2 z ) (x + w 2 y + w z) を使う
こ の 公 式 ははじめて 見 る ので 検 証 してみました
( x + w y + w 2 z) ( x + w 2 y + w z )
= x 2 + w x y + w 2 x z
+ w 2x y +w 3 y 2 +w 4 z y
+ w x z + w 2 y z +w 3 z 2
= ( x 2 +w 3 y 2 + w 3 z 2 ) + 【 ( w + w 2 ) x y + ( w 2 + w 4 ) y z + ( w + w 2 ) z x】
w 2 + w + 1 = 0 w = ( - 1 + i √3 ) / 2 w 2 = ( - 1 - i √3 ) / 2
w 3 = 1 ( w + w 2 ) = ( w 2 + w 4 ) = - 1
= ( x 2 + y 2 + z 2 ) - ( x y + y z + z x )
結 局 公 式 B と 同 じ 形 となりました 納 得
公式 B x 3+y 3+z 3 - 3 x y z = ( x + y + z ) ( x 2 + y 2 + z 2 - x y - y z - z x )
公式 C x 2 + y 2 + z 2 = ( x + y +z ) 2
- 2 ( x y + y z + z x )
x 3 - 3 x y z + ( y 3 + z 3 )
y 3 + z 3 = q
y 3 、 z 3 の 連 立 方 程 式
- 3 y z = p ⇔ y 3 z 3 = p 3 / 27
この 連立方程式 は 2 次方程式 の 解 と 係 数 の 公 式 と 同 形 です
2 次方程式 f (x) = x 2 + a x + b = 0 の 解 を α β と すると
α + β = - a αβ = b
従って y 3 z 3 を 解 とする 2 次方程式 が 作れる ことになる
ζ 2 - q ζ - p = ζ 2 - ( y 3 + z 3 ) ζ + ( y 3 z 3 )
ζ = ( ( y 3 + z 3 ) ± √ 【 ( y 3 + z 3 ) 2 - 4 y 3 z 3 ) 】 ) / 2
ζ = ( p ± √ 【 p 2 - 4 q 3 ) 】 ) / 2
この式の根 は x = - ( y + z ) 、 - ( w y + w 2 z ) 、 - ( w 2 y + w z )
y と z を 代 入 すれば o k
3 次方程式 の 解 の 公 式 ( ガロア理論 ) Youtube 動 画
3 次方程式 の 解 ( 物 理 の かぎしっぽ )
3 次方程式 の 解 と その他の 解 (高校数学 Ⅱ)
● フォンタナ(Nicolo Fontana)
(1499―1557)

イタリアの数学者。子供のとき、ブレシアへ侵入してきたフランス兵に父を殺され、
自らも舌を切り取られた。そのためものをいうことが不自由であり、
「タルターリア」Tartaglia(イタリア語で「どもり」の意)とあだ名された。独学で数学を身につけ、
ベローナ、ブレシア、ベネチアの各大学で教授となっている。
三次方程式x3+px=q(この時代には式はなくことばで示されていた)の解法を樹立。
この解法を公表しないという条件で請われるままにカルダーノに教えたところ、カルダーノは
約束を違えて、1545年に出版した著書『すばらしい技術、すなわちアルゲブラの規則について』
のなかで公表してしまった。現代の数学で「カルダーノの公式」とよんでいるものは、
フォンタナのものである。 [小堀 憲][参照項目] |
● カルダーノ Girolamo Cardano (1501―1576)

イタリア・ルネサンス期の医学者、自然主義的哲学者、数学者。ミラノ近くのパビアに私生児として生まれ、
母親の不安定な愛情のため、悲しい少年期を送る。パビア、ミラノ、パドバで学び、パビア、ミラノ、
ボローニャで医学を教える。いわゆる「カルダーノの公式」によって数学者として広くヨーロッパに知られた。
70歳で投獄、異端審問にかけられるが、晩年はローマで過ごした。
その特異な性格は、1542年に書かれ死後出版された『自伝』(1643)にうかがわれる。
きわめて旺盛(おうせい)で広範な知識欲をもち、占星術、魔術などに関する著作のほか、
とくに哲学的な主著としては、百科全書ともいうべき『不思議について』(1550)、
『事物の雑多について』(1557)があり、そこにはルネサンスに固有な矛盾が典型的な形で現れている。
アニミズム的立場から、一方では新プラトン主義的伝統に従って、魔術のもつ思弁的価値を認めながら、
他方、物質自体のなかに生命の原理をみいだし、人間を頂点とする進化論的な考えをとる。
そのためアリストテレスに反し、物質に活動的な特徴を認めることによって、内在論的・進化論的自然観へ
と向かう一方、自然の絶対的な一つとしてのまとまりを、霊という超自然的原理に求めざるをえないことから
、超越論的自然の形而上(けいじじょう)学にもなっている。人間の霊魂についてアベロエス(イブン・ルシュド)
的解釈をとる。[大谷啓治]
1545年に『すばらしい技術、すなわちアルゲブラの規則について』Artis magnae, sive de regulis
algebraicisを出版、このなかに三次方程式における「カルダーノの公式」がある。
この方法はタルターリア(フォンタナ)が樹立した公式で、彼がカルダーノに、他人に教えないことを条件とし
て教えたのであるが、その約束を破って上記の著書に公表してしまい、発表者の名をつける習慣から
「カルダーノの公式」と名づけられた。カルダーノの公式は、その当時には式はなく、
ことばで示されているが、現代の式で示すと、三次方程式 x3+px=q の根が
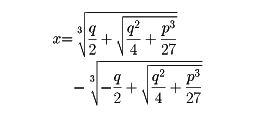
であることを示したものである。[小堀 憲]
『カルダーノ著、青木靖三・榎本恵美子訳『わが人生の書――ルネサンス人間の数奇な生涯』
(1980・社会思想社/1989・現代教養文庫) ▽清瀬卓・澤井繁男訳『カルダーノ自伝』(1995・平凡社)』
x 3 + a x 2 + b x + c = 0 の 解
X1 = u1 + v1 - a/3
=ω1×(ξ1)1/3+ω1×(ξ2)1/3-a/3 p = b/3 -
a2/9
=1×[-q+√(q2+p3)]1/3+1×[-q-√(q2+p3)]1/3-a/3 q = c/2 + a3/27
-a.b/6
=(27c+2a3-9ab)/54
=【-(27c+2a3-9ab)+《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3》1/2】1/3
+【-(27c+2a3-9ab)-《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3 》1/2
】1/3 - a/3
X2 = u2 + v3 - a/3
=ω2×(ξ1)1/3+ω3×(ξ2)1/3 - a/3
=(-1+ i √3)/2 ×【-(27c+2 a3 -9ab)/54+《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3》1/2】1/3
+ (-1-i √3)/2 ×【-(27c+2a3-9ab)-《〈(27c+2a3-9ab)/54〉2+〈(3b-a2)/9〉3 》1/2
】1/3 - a/3
X3 省 略

