np - 160

　　　　　　　　　 Γ( z ) = ∫₀ ^∞ t ^{( z-1)} . e ^{- t} d t 　=　 ( e^-t ) t ^{( z-1 )} 　- ∫₀^∞ 　(e^-t ) (z - 1) t ^{(z - 2)} dt

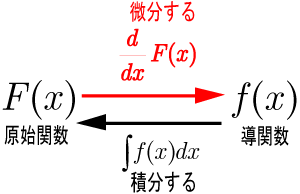
　　　　　　　　　　　　　　　　　　↑　g ( x )　　　↑　f ( x )　　　　　　↑　F ( x )　　↑　g ( x )　　　　　　　　　↑　F ( x )　　　 ↑ g ゜ ( x )


　　　　　　　　　　　　　　部 分 積 分　　∫ f ( x ) g ( x ) d x = F ( x ) g ( x ) 　- 　∫ F ( x ) g ｀( x ) d x

　　　　　　　　　　　　　　積 分 しやすい方 を　　f ( x )　　として　　　　　　微 分 しやすい方 を　　g ( x ) 　とする


　　　●　　　　ガ ン マ　関 数　　　　　　　


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　 　　　　　　　　　　　　　　　　　ルジャンドル　(フランス) 　 　 　　　　1 8 世 紀　　　　　　オイラー　　　(スイス　→　ロシオ)


　　　　　　数 学 において ガンマ 関 数 （ 英: Gamma function ） とは、【　階 乗 の 概 念 を一般化した 特 殊 関 数　】 である。


　　　　　　互いに同値となるいくつかの定義が存在するが、1729年、数学者　 オイラー　が階乗の一般化として、最初に導入した。


　　　　　　　　　実部が正となる複素数 z について、次の積分で定義される関数

　　　　　　　　　　　　　　　


　　　Γ( z ) = ∫₀ ^∞ t ^{( z-1)} . e ^{- t} d t 　=　 ( e^-t ) t ^{( z-1 )} 　- ∫₀^∞ 　(e^-t ) (z - 1) t ^{(z - 2)} d t

　部 分 積 分　　∫ f ( x ) g ( x ) d x = F ( x ) g ( x ) 　- 　∫ F ( x ) g ｀( x ) d x

積 分 しやすい方 を　　f ( x )　　として　　　　　　微 分 しやすい方 を　　g ( x ) 　とする

　　　　　f ( x ) = e ^{- t}　　　F ( x ) = ∫ f ( x ) d x = e ^{- t} 　　　　g ( x ) = t ^{( z - 1 )} 　　　g ゜( x ) = ( z - 1 ) t ^{( z - 2 )}

　　　　　　　　　　　　e ^{(-- t)} 　の 微 分　　 e ^{(- t)}　　　　　　　t ^{( z- 1 )}　の 微 分　　( z - 1 ) t ^{(z - 2)} 　　


　　　　　　　　　　　　　　　　　　　　　部 分 積 分 法　　　　Youtube


　　　　　　　　　　　　　　　　　　　積 分 の 公式集　　 　　　　　　　　　微 分 の 公式集


　　　　　　　　　　　　　　　　　　　　　　　　　　

　　－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－


　　　　　追　　記　　　2017　９　４　　　部 分 積 分 の 計 算　 例

　　　部分積分の公式　　∫ f ( x ) g ( x ) d x = F ( x ) g ( x ) 　- 　∫ F ( x ) g ｀( x ) d x


　　　　　　　　問 題　－　１　　∫x e^x d x

　　　　　　　　　　　　　　　　　f (x) = x 　　　　g (x) = e ^x　　として　計算　した　場　合


　　　　　　　　　　　　　　　　　f (x) = e ^x　　　 g (x) = x　　　として　計算　した　場　合


　　　　　　　　問 題　－　２　　∫x cos x d x　　


　　－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－　

　　　　　Г( z )　を ガンマ 関数 と呼ぶ^[1]。この積分は、ルジャンドルの定義にしたがって、第二種 オイラー積分 とも呼ばれる。

　　　　　　元は階乗の一般化としてオイラーが得たもので、Γ という記号は、ルジャンドルが用いたものである。

　　　　　　それ以前は Π(x) などと表記していた（ただし Π(x) = Γ(x + 1)）。

　　　　　　　　　　　一般の複素数 z については、解析接続 もしくは次の 無限乗積 で定義される

　　　　　　　　　　　　　　　　　


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　ルジャンドル　(フランス) 　 　 　　　　1 8 世 紀　　　　　オイラー　　　(スイス　→　ロシオ)


　　　　　　　　　　　
　　　　　　　　　　　　 　　　　　　　　　　
　　　　　　　
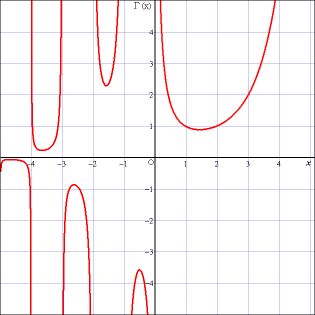
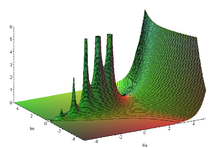
　　　　　　　　　　　　　ｙ　＝ Γ ( x ) 　の　グラフ　　　　　　　　　　　Γ( x + i y ) 　の　絶対値　Re は　に相当　I m は　に　相当


　　　　　　　　　　　　　　　　　　　　　　　　　　　　y = Γ x　　　の　グラフ　を　作る　


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　


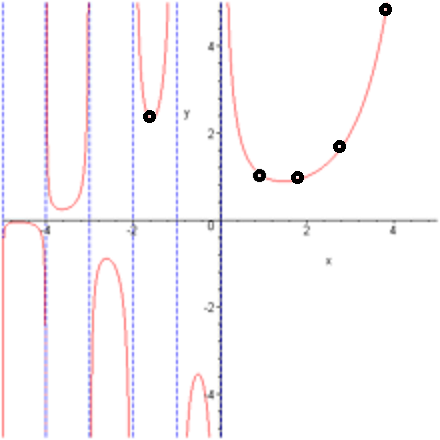
　　　　　　　　　　　　　　　　テキスト　に　ある　グラフ　　の　上に　計 算　結 果　を　プロツト　してみる


　　　　　　　　　　　　　－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
　　　　　　　　　　　　
　　　　　　　　いくつか　の　具 体 的 な 値 　[編集]


　　　　　　　　　　　　　　Γ( x + 1)　=　x Γ( x )
(− 32 ) = 4 π 3 ≈2.363 {\displaystyle \Gamma \left(-{\frac {3}{2}}\right)\,={\frac {4{\sqrt {\pi }}}{3}}\approx 2.363\,}

　　　　　　　　　　Γ ( - 3/2 )　=　 4 √π　≒　2.363

Γ (− 12 ) =−2 π ≈−3.545 {\displaystyle \Gamma \left(-{\frac {1}{2}}\right)\,=-2{\sqrt {\pi }}\approx -3.545\,} Γ ( 12 ) = π ≈1.772 {\displaystyle \Gamma \left({\frac {1}{2}}\right)\,={\sqrt {\pi }}\approx 1.772\,} Γ ( 1 ) =0!=1 {\displaystyle \Gamma (1)\,=0!=1\,}
　　　　　　　　　　Γ　( - 1/2 ) 　=　- 　2 √π　≒　- 3.545
Γ ( 32 ) = π 2 ≈0.886 {\displaystyle \Gamma \left({\frac {3}{2}}\right)\,={\frac {\sqrt {\pi }}{2}}\approx 0.886\,}
${\displaystyle \Gamma (2)\,=1!=1\,}$
${\displaystyle \Gamma \left({\frac {5}{2}}\right)\,={\frac {3{\sqrt {\pi }}}{4}}\approx 1.329\,}$　　　　　　　　　　Γ　( 1/2 ) 　=　 √π　=　1.772
${\displaystyle \Gamma \left({\frac {7}{2}}\right)\,={\frac {15{\sqrt {\pi }}}{8}}\approx 3.323\,}$
${\displaystyle \Gamma (4)\,=3!=6\,}$
　　　　　　　　　　Γ　( 1 ) 　=　0 ！　= 　1


　　　　　　　　　　Γ　( 3/2 ) 　=　 √π / 2 　≒　o.886


　　　　　　　　　　Γ　( 2　) 　=　0 ！　= 　1


　　　　　　　　　　Γ　( 5/2 ) 　=　3 √π/4　≒　1.323



　　　　　　　　　　　ガンマ　関　数　　高 精 度 計 算　　　　　Yahoo


　　　　　　　　　　　　　keisan　

　　　　－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－


　　　　　　　　　　　階 乗 の 正 体　は　ガンマ 関 数 　　Youtube


　　　　　　　　ガンマ 関 数 の 具 体 的 計 算 例　Γ( 3 / 2 ) 　= .√π / 2 　とあるが

　　　　　　　　どうしても　導 出　できませんでした

　　　　Yahoo　・　 Youtube　では　詳しく　丁 寧 に　説 明 しているので 理 解 することができました


　　　　　◆　　　階 乗　の　一 般 化　　　　　Yahoo　　よ　り


　　　　　　　　　　Γ・　ガンマ　関 数　の 手 計 算　に　挑 戦　し ま す
　　　　　　
　　　　　　　　　Γ( z )　=　∫₀^∞ 　t ^{( z - 1 )} ・ e ^{- t} d t　　


　　　　　　　　　部 分 積 分

　　　　　　　∫f (x) ・ g (x) d x　=　F (x) ・ g (x)　-　∫F (x) ・ g゜(x) d x

　　　　　　　積 分 しやすい 方 　を　f (x)　と し 。　微 分 しやすい 方 　を　g (x)　 とするのが　コ ツ　　

　　　　　　　　f (x) = e^{- t} 　　F (x) = e^{- t}　　　　g (x) = t (x - 1) 　　　g゜(x) =　(x - 1) t ^{(x - 2)}　


　Γ( z ) = ∫₀ ^∞ t ^{( z-1)} . e ^{- t} d t 　=　 ( e^-t ) t ^{( z-1 )} 　- ∫₀^∞ 　(e^-t ) (z - 1) t ^{(z - 2)} d t

　　　　　　　
　　　　　　　　　　Γ (1) = ∫₀^∞　t^{(1 - 1)} e ^{- t} d t　=　∫₀^∞　 e ^{- t} d t　=　【- e^-t　】₀^∞　=　1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　= ∫₀^∞ t ⁰ e ^{- t} d t = ∫₀^∞ 1 × e ^{- t} d t = 　e ^1/t d t　=　【- e^-t　】₀^∞　=　1
　　　　　　　　　　Γ (2) = ∫₀^∞ 　t e ^{- t} d t　=　【　- t e^-t 】 _o^∞　+　∫₀^∞　 e ^{- t} d t　=　1

　　　　　　　　　　Γ (3) = ∫₀^∞　t² e ^{- t} d t　=　【　- t ² e^-t 】 _o^∞　+　2∫₀^∞　 t e ^{- t} d t　=　2　

　　　　　　　　　　Γ (4) = ∫₀^∞　t³ e ^{- t} d t　=　【　- t ³ e^-t 】 _o^∞　+　3∫₀^∞　 t² e ^{- t} d t　=　6


　　　　　　となる 計 算 からも 分かる ように、

　　Γ(４)＝３！＝３・２・１＝６　、Γ(３)＝２！＝２・１＝２　、Γ(２)＝１！＝１　、Γ(１)＝０！＝１

　　に相当していることがうかがえる。　一般に、漸化式

　　　　　　　　　

　　が成り立つので、ｘ が自然数 ｎ のとき、　Γ(ｎ＋１)＝ｎ！　となる。

　　したがって、ガンマ関数は、自然数 ｎ に対して、ｎ！を対応させる関数（定義域は自然数

　　全体）を正の実数全体を定義域とする関数にまで拡張したものと考えることができる。

　　この意味で、　『　Γ(ｘ＋１)＝ｘ！　』　と書くことも可能ではないだろうか？

　　たとえば、　冒頭の　（１/２）！は、
　　　　　　　　　　　　　　　　　　　　　　　　　
　　　となる。　実際に、

　　　　　

　　　において、
　　　　　　　　　　　　　　　　　
　　　と変数変換すれば、
　　　　　　　　　　　　　　　　　
　　　であるので、
　　　　　　　　　　　　　　　　
　　　となる。

　　　　　（→　参考　：　無限の拡がりをもつ面積 １ の図形について）

　　　読者に対して、練習問題を残しておこう。

　　　問題　　（３/２）！　はいくらであるか？

　　　 （追記）　当ＨＰがいつもお世話になっているＨＮ「攻略法」さんに解いていただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２２年１０月１４日付け）

　　　（解）　（３/２）！＝Γ(３/２＋１)＝３/２Γ(３/２)

　　　ここで、Γ(３/２)＝Γ(１/２＋１)＝（１/２）！＝（√π）/２　なので、

　　　　　　（３/２）！＝３（√π）/４　　（終）

　　　（コメント）　解答をお寄せいただいた攻略法さんに感謝します。


　　　　　（参考文献：黒川信重　著　数学の夢　素数からのひろがり　（岩波書店））


　　　この 資 料 で　ようやく　ガンマ関数 が 手 計 算 できるよう になりました



　　　　　◆　　　以 下　　　　Youtube

　　　　　　　n ！ = 　n ( n - 1 ) ( n - 2 ) ( n - 3 ) ・　・　・　　1

　　　　　　　　　　3 ！　= 　3 × 2 × 1　　　　　　　　 0 ！　=　 1

　　　　　　Γ (n + 1) 　= 　n ！

　　　　　　Γ (n + 1 ) 　= 　∫　tⁿ e^-t dt = 【　tⁿ (- e^-t)　】 - ∫₀ ^∞　t^(n-1) (-e^-t) dt

　　　　　部分積分　∫　f (x) g (x) dx 　= 　F (x) g (x) - ∫ F (x) g゜ (x) dx


　　　　　　Γ ( n + 1 ) 　= 　∫₀ ^∞ t ⁿ ・ e^-t d t 　　　( n ＞ 0 )　

　　　　　　　　　　　 = 　【 tⁿ ( -e^-t ) 】₀ ^∞　- ∫₀ ^∞ 　n t^(n-1) ( -e^-t ) d t

　　　　　　　　　　　 = 　【 - tⁿ ・ e^-t 】₀ ^∞ + n ∫₀ ^∞ 　t^(n-1) ・ e^-t d t

　　　　　【 - tⁿ ・ e^-t 】₀ ^∞ =　　【-tⁿ / e^t　】₀^∞ 　=　 -∞ⁿ / e∞ 　- 　(- 0ⁿ / e^o)

　　　　　　　　lim _t→∞　-tⁿ / e^t 　=　 lim _t→∞ 　o / e^t 　= 　o / ∞ 　= 　o　


　　　　　Γ ( n + 1 )　 = 　∫₀ ^∞ tⁿ e^-t dt = n ∫₀ ^∞ tⁿ e^-t dt = n Γ ( n )

　　　　　Γ　(n + 1 )　 = 　n Γ ( n ) = n ×( n - 1 ) Γ ( n - 1 )

　　　　　　　　　　　　 = 　n × ( n - 1 ) × ( n - 2 ) Γ ( n - 2 )　　

　　　　　　　　　　　　 = 　n × ( n - 1 ) ×( n - 2 ) ×・・・　×　1 Γ ( 1 ) 　= 　n ！

　　　　　Г ( 0 + 1 ) 　= 　Г ( 1 ) = 0 ！ = 1

　　　　　( 1 / 2 ) ！　 =　 Γ( 3 / 2 ) = ∫₀ ^∞ t ^{( 1/2)} e^{- t} dt　= ∫₀ ^∞ 　√t e^{- t} dt

　　　　　　　　　　　　 = 　【 - √t 　e^-t dt 】 - ∫₀ ^∞　( - 1 / 2 √t ) e^-t

　　　　　　　　　　　　 = 　【 - √t 　e^-t dt 】 + ∫₀ ^∞　( 1 / 2 √t ) e^-t

　　　　　　　x 　= 　t^1/2　　dx / dt 　=　 (1/2) 　t^-1/2 　=　 1 / 2 √t

　　　　　　　dx 　=　 dt / 2 √t

　　　　　( 1 / 2 ) ！　=　 ∫₀ ^∞　e^-x2 dx

　　　　　I 　= 　∫_-∞ ^∞　e^-x2 dx　　×　　I 　= 　∫_-∞ ^∞　e^-y2 dy

　　　　　I ² 　= 　∫_-∞ ^∞ 　∫_-∞ ^∞　e^{-(x2 + y2)}dxdy　=　π

　　　　　　I 　=　 √π

　　　　　　　x 　=　 r cosθ　　y 　=　 r sinθ　　x² + y² =　 r²

　　　∂ r cos θ/ ∂θ　　∂ r cos θ/ ∂θ　　　　　　　cos θ　 - r sin θ
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　行列式　　　= 　r cos² θ + r sin² θ 　= 　r
　　　∂ r sin θ/ ∂ r　　∂ r sin θ / ∂ r　　　　　　　 sin θ 　 r cos θ


　　　I ² 　= 　∫_-∞ ^∞ 　∫_-∞ ^∞　e^{-(x2 + y2)}dxdy = ∫₀^2π ∫₀^∞ 　e^-r2 r d r dθ

　　　　　　= ∫₀^{2π 【　(- 1/2 ) 　e-r2 】 ₀∞ dθ}

　　　　　　= ∫₀^2π　(1/2 ) d θ　= 　【 (1/2) θ】₀^2π = π　　　　I 　=　 √π


　　　　　　　　　　　 (1/2) ！ = (√π) / 2　　　　　　


　　ー　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー



　　　　　ガンマ 関 数 　の　 勉 強 を 始 め た 時　　資 料 の 冒 頭 に　


【　ガンマ 関 数 は 階 乗 の 概 念 を 一 般 化 し た　特 殊 関 数 で あ る　】　　と あ り ま し た


　　　全 般 が ほぼ 理 解 できた 今　　この 意 味 が分かりました　　　欲 求 不 満　解　消



尚 　ベツセル 関 数　ベータ 関 数　等 は　ガンマ 関 数　の 延 長 線 　にあるので　親 し み　やすくなりました



　　－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－ーーーーーーー


　　　　　◆　　　Γ　ガンマ　関 数　　は　いろんな 関 数 式　に 現 れ る　

　　　　　　　　他 の　特 殊 関 数 も ガンマ 関 数 の 線 上 にあるものが多 く　親 しみ やしくなりました


　　　　　　　　ベッセル　　関 数

　　　　　　　　　　　　　Jα (x) 　=　 (-1)m 　/　【 　m！　( Γ( m + α+ 1 ) )　 】　^_(x/2)2m+α

　　　　　　　　β　　関　数　　と　　Γ関 数　の　関 係

　　　　　　　　　　　　　B ( x 、y ) 　=　 【　Γ(x) 　Γ(y)　】　 / 　Γ( x + y )

　　　　　　　　ワイブル　分　布　　

　　確率分布 より　その　密度関数 は　【　【 Γ( n/2 + 1/2 ) 】　 / 　【 (√nπ) Γn/2 】 】 【 1 + x² / n 】^{- (n+1)/2}



　　－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－


　　　　　　　　　　　　　　◆　 　特 殊 関 数　の　応 用 　


　　　　　　　　　　ガンマ　関数　（Ｇａｍｍａ　ｆｕｎｃｔｉｏｎ）は、次式　で　定義　される。

　　　　　　　　　ｓ＞０　に対して、
　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　ガンマ関数については、　Γ（１）＝１　は明らかだが、次の例が最も有名であろう。

　　　　　　　　　　　　
　　　　　　　　例　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　

　　　　　　ここで、
　　　　　　　　　　　　　　　　　

　　　　　　とおくと、
　　　　　　　　　　　　　　
　　　　　　よって、