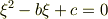私 は 高 校 生 時 代 特 種 関 数 は 分からない も の と 気 嫌 い しておりました
ガンマ 関 数 ベツセル 関 数 ベーター 関 数 確 率 密 度 関 数 等
今 回 暇 つ ぶ し に 挑 戦 してみました
Yaho Youtube 等 よ り いろんな 資 料 を 拾 い 勉 強 しました
2 ケ 月 以 上 かかつて ようやく ほ ぼ 理 解 できました
8 0 才 過 ぎ た 今 こんなに 辛 抱 強 い と は 一 人 に が 笑
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
● 一 次 関 数 二 次 関 数 三 次 関 数
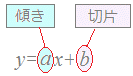
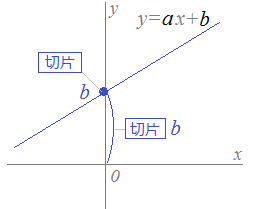
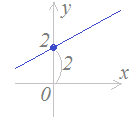
一 次 関 数 y = a x + b
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
二 次 関 数 y = a x 2 + b x +c
二次方程式 の 解 は 古 代 バ ビ ロ ニ ア で 数 千 年 前 に 発 見 されていた
古 代 バ ビ ロ ニ ア 現 在 の イ ラ ク の 位 置
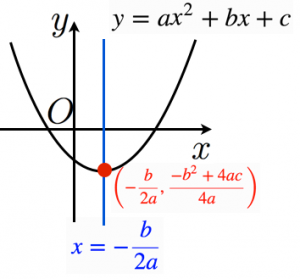
二 次 関 数 y = a x 2 + b x + c に お い て,
二次方程式 の 解 は α . β = 【 - b + - √ ( b2 - 4ac ) 】 / 2a)
頂 点 の 座 標 は - b / 2 a ・ ( - b 2 + 4 ac ) / 4 a
軸 の方 程 式 は x = - b / 2 a
解 と 係 数 の 関 係 式 は α + β = - b / a α × β = c / a
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
追 記 遇 関 数 奇 関 数
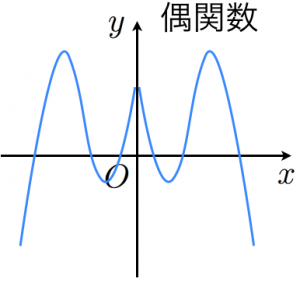
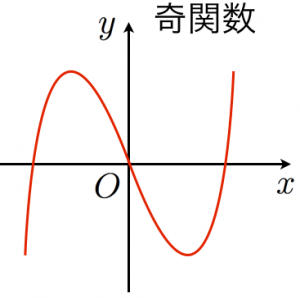
遇 関 数 は f (x) = f (-x) を 満 た す y = f (x) グラフ が y 軸 に 関 し て 対 象 である
x の 偶 数 乗 の 項 の み で 構 成 さ れ た 関 数
奇 関 数 は f (x)=- f (-x) を 満 た す グラフ が 原 点 に 関 し て 対 象 で あ る
x の 奇 数 乗 の 項 の み で 構 成 さ れ た 関 数
● 遇 関 数 ・ 奇 観 数 と 定 積 分
f (x) が 遇 関 数 の と き ∫-aa f (x) d x = 2∫0a f (x) d x
f (x) が 奇 関 数 の と き ∫-aa f (x) d x = 0
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
三 次 関 数 y = a x 3 + b x 2 + c x + d
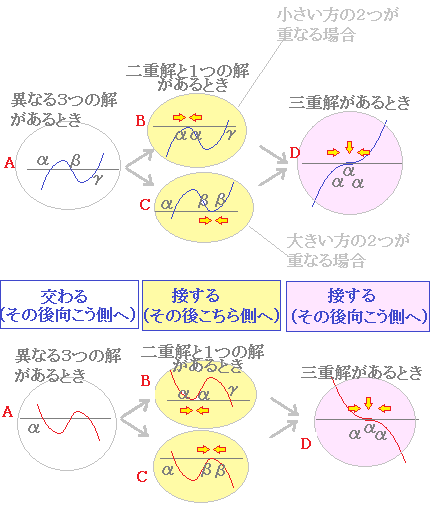
◆ 三 次 方 程 式 の 解 カルダノ の 公 式 M y - H P
1 6 世 紀 1545


フォンタナ (タルタニア) 伊 カルダノ に 騙 さ れ た タルタニア が 怒 っ て い る
私 は 三 次 方 程 式 の 解 は カルダノ の 公 式 で 勉 強 し ま し た
式 の 展 開 は 機械的 に 追える のですが な ぜ そのように するのか 分からない ところが 多 く ありました
日 に ち おおいて 繰り返し 読んでいるうちに あ っ そうだったのかと 気づく ところが でてきました
一か月 くらいして ようやく 全 体 が 理 解 で き ま し た
三 次 方 程 式 の 解 の 求 め 方
二次方程式 の 解 お求める ときに y = a x 2 + b x + c = 0 の 式 お
平 方 完 成 の 式 ( x + b ) 2 = ( b 2 - 4 a c ) / 2 a に 変 換 して この 式 の 両 辺 の 平 方 根 おとって
α ・ β = 【 - b + - √ ( b2 - 4ac ) 】 / 2a )
三次方程式 の 解 も 同 様 に a x 3 + b x 2 +c x + d = 0 お 変数変換 して 立 体 完 成 の 式 お作る
y = ( x + a / 3 ) とすると y 3 + 3 p y + 2 q = 0 3 p = b - a 2 / 3 2 q = c + 2 a 3 / 27 - a b / 3
y 2 の 項 が 消 え て い る
更 に y = u + v と 変 数 変 換 して
y 3 + 3 p y + 2 q = ( u + v ) 3 + 3 p ( u + v ) + 2 q
= u 3 + 3 ( p + u v ) + v 3 + 2 q = u 3 + 3 ( p + u v ) ( u + v ) + v 3 + 2 q = 0
ここで 上 の 等 式 が 成 り 立 つ ためには 次の二式が 成り立てば良い
u 3 + v 3 + 2 q = 0 u 3 + v 3 = - 2 q
( p + u v ) ( u + v ) = 0 u v = - p u 3 ×v 3 = - p 3
u 3 と v 3 お 解 とする 次 の 二 次 方 程 式 が 得 ら れ ま
ζ2 + 2 q ζ - p 3 = 0 元 の 三 次 方 程 式 の 分 解 方 程 式 と よびます
ζ = 【 - 2 q +- √ ( 4 q 2 + 4 p 3 ) 】 / 2 = - q +- √ ( q 2 + p 3 )
ζ = u 3 ・ v 3 なので
u 3 = - q + √ ( q 2 + 4 p 3 )
v 3 = - q - √ ( q 2 + 4 p 3 )
u 3 ・ v 3 は 三 次 方 程 式 なので それぞれ 3 個 の 解 お 持つはずです
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
追 加 分 解 方 程式 ζ2 + 2 q ζ - p 3 = 0 がなぜ 作れるのか 分かりませんでした
掲 示 板 物 理 の かぎしっほ に 質 問 したらすぐ 次 の ような 答 え が きました
u 3 + v 3 = - 2 q u 3 ×v 3 = - p 3 こ の 2 式 は
2 次 方 程 式 の 解 と 係 数 の 形 と 同 じ で し た 納 得
三次方程式
三輪次男 さん の 書込 (2008/04/24(Thu) 09:08)
教えてください 三次方程式の解の公式Jon @ 物理のかぎプロジエクト
3ペ−ジのなかほどに U^3 + V^3 = -2q U^3 V^3 = -p^3と 分解方程式(2次方程式)ξ^2 + 2qξ - p^3 との関係について
この関係はどのようにして導かれるのでしょうか? 素人に分かるようにやさしく教えてください08−04−24
Re: 三次方程式
三輪次男 さん の レス (2008/05/01(Thu) 14:05)
ご教授ありがとうございました. 私は不勉強でこの関係を知りませんでした.
三次方程式の解の公式を勉強していたときこの関係が理解,納得できず いらいらして欲求不満になっておりました.
おかげさまですっきりしました. 多 謝 08−05−01
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
つ づ き
( 代数学 の 基本定理 によれば n 次 方 程 式 は ・ 複 素 数 の 中 に n 個 の 解 お 持つちます と あります )
従って u 1 = w 1 3 √ 【 - q + √ ( q 2 + p 3 ) 】 v 1 = w 1 3 √ 【 - q + √ ( q 2 + p 3 ) 】
u 2 = w 2 3 √ 【 - q + √ ( q 2 + p 3 ) 】 v 2 = w 2 3 √ 【 - q + √ ( q 2 + p 3 ) 】
u 3 = w 3 3 √ 【 - q + √ ( q 2 + p 3 ) 】 v 3 = w 3 3 √ 【 - q + √ ( q 2 + p 3 ) 】
w1 = 1 w2 = ( - 1 + i √3 ) w3 = ( - 1 - i √3 ) の 説 明
x 3 = a 3 因数分解 で 解 お 求めてみる と
( x - a ) ( x 2 + a x +a 2) → x1 = w1 a x2 = w2 a = ( - 1 + i √3 ) a x3 = w3 a = ( - 1 - i √3 ) a
y = u + v なので u + v は 次 の 9 通 り あります
u 1 + v 1 u 2 + v 1 u 3 + v 1
u 1 + v 2 u 2 + v 2 u 3 + v 2
u 1 + v 3 u 2 + v 3 u 3 + v 3
ところが u 3 + v 3 = - 2 q u 3 v 3 = - p 3 お 満 足 する ものは 次 の 3 通 り で す
y 1 = u 1 + v 1 y 2 = u 2 + v 3 y 3 = u 3 + v 2
立 体 完 成 のところで y = x + a / 3 と置いたので 逆変換 して x の 解 お 求める
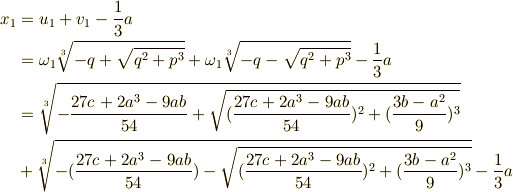
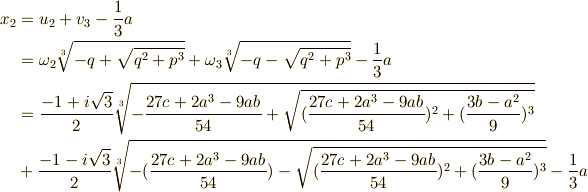
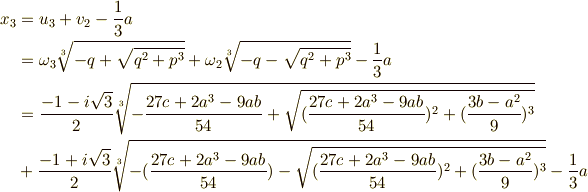
-----------------------------------------------------
● 四 次 方 程 式 Wikipedia
一 変 数 の 四 次 方 程 式 は
- a4 x4 + a3 x3 + a2 x2 + a1 x + a0 = 0, (a4 ≠ 0)
の形で表現される。 a4 で割 り
- x4 + A3 x3 + A2 x2 + A1 x + A0 = 0, ( An = an / a4)
の形にしても根は変わらないのでこの形で論じられることが多い。
一 般 的 な 四 次 方 程 式 の 解 法 は
、 カルダノの弟子であるルドヴィコ・フェラーリ, 1522-1565)によって発見され、
カルダノの著書『アルス・マグナ』で概要が述べられた。
カルダノは x, x2, x3 を、線分の長さ 一辺の長さが x の正方形の面積、
一辺の長さが x の立方体の体積と対応させてとらえ、
4 次以上の方程式には意味がないと考えていたため、
三次方程式と違って詳細には述べられていない。
しかし、カルダノの死後、デカルトは著書『方法序説』において定規とコンパスによる作図を論じ、
長さ x の線分、長さ y の線分、長さ 1 の線分から長さ x y の線分が得られることを示している。これによると、
長さ x の線分と長さ 1 の線分から長さ xn ( n は任意の自然数)の線分の作図が可能であることが分かるため
4 次以上の方程式を解くことにも幾何学的な意味を与えることは可能であり、カルダノのとらえ方は不十分であったことが分かる。
その後、四次方程式は三次方程式と同様に様々な解法が発見され
、五次方程式の代数的解法の探索と合わせて詳細な研究が進められた。
複 二 次 式 [編集]
四次方程式 の 内 奇 数 次 の 項 が 無 い
- a4 x4 + a2 x2 + a0 = 0 (a4 ≠ 0)
の形の式は x2 を変数とする 二次方程式 と見ることができ、複二次方程式 あるいは単に複二次式と呼ばれる。
二次方程式の解法を知っていれば簡単に解くことができる。
y = x2 と変換することで y に関する二次方程式
- a4 y2 + a2 y + a0 = 0
を得ることができ、この二次方程式を解くことによって根を求められる。 a4で割る。An=an/a4
また、実数を係数とする複二次式
- x4 + A2 x2 + A0 = 0
-------------------------------------------
補 足 x4 + A3 x3 + A2 x2 + A1 x + A0 = 0, ( An = an / a4)
x4 + A2 x2 + A0 = 0 を 導 出 す る
参 考 ( a ± b ) 1 = a ± b
( a ± b ) 2 = a 2 ± 2 a b + b 2
( a ± b ) 3 = a 3 ± 3 a 2 b + 3 a b 2 ±+b 3
( a ± b ) 4 = a 4 ± 4 a 3 b + 6 a 2 b 2 ± 4 a b 3 + b 4
-------------------------------------------
に対して、次のような二次式の積への因数分解もよく行われる。 x2 の二次方程式とみたときの判別式
- D = A22 − 4 A0
の符号によって
D > 0 であれば x2 について 平方完成 することにより
x 4 + A2 x 2 + A0 = ( x 2 + A2 / 2 ) 2 - ( A2 2 - 4 A0 ) / 4
D < 0 であれば A0 > 0 であることに注意して
x 4 + A2 x 2 + A0 = ( x 2 + √A0 ) 2 - ( 2 √A0 - A2 ) x 2
と変形すれば、いずれの場合も 因数分解 の公式
- α2 − β2 = (α + β) (α − β)
を利用して 実 数 を 係 数 とする 二 次 式 の 積 に 因 数 分 解 できる
-----------------------------------------------------
● 五 次 方 程 式
-----------------------------------------------------
● 指 数 関 数 と 対 数 関 数 ← M y H P 参 照
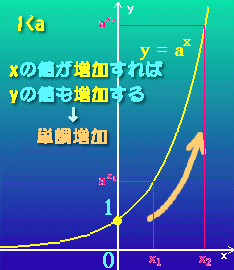
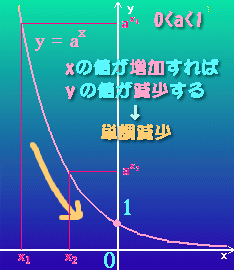
y = a x の y = loga x グ ラ フ
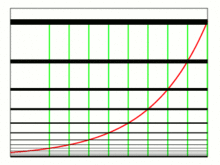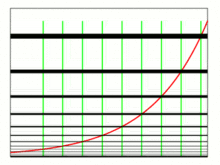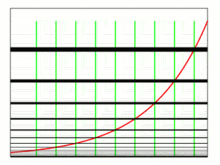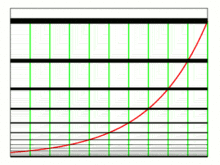
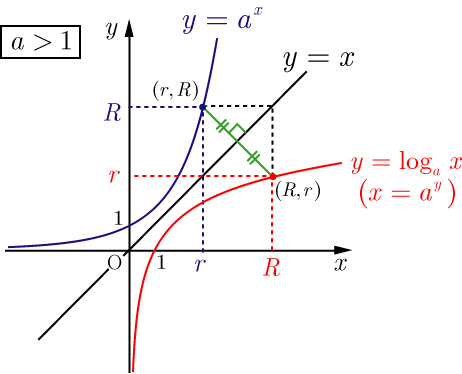
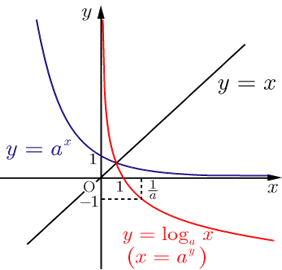
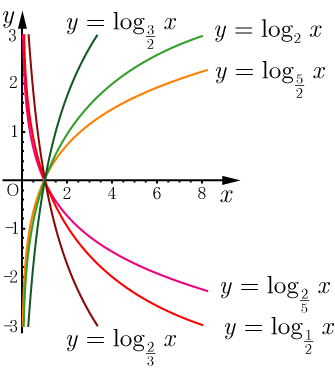
a > 1 0 < a < 1 a < 1 または a < 1
------------------------------------------------------
● ガ ン マ 関 数


ルジャンドル (フランス) 1 8 世 紀 オイラー (スイス → ロシオ)
数 学 において ガンマ 関 数 ( 英: Gamma function ) とは、【 階 乗 の 概 念 を一般化した 特 殊 関 数 】 である。
互いに同値となるいくつかの定義が存在するが、1729年、数学者 オイラー が階乗の一般化として、最初に導入した。
実部が正となる複素数 z について、次の積分で定義される関数
Γ( z ) = ∫0 ∞ t ( z-1) . e - t d t = ( e-t ) t ( z-1 ) - ∫0∞ (e-t ) (z - 1) t (z - 2) d t
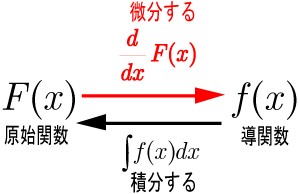
部 分 積 分 ∫ f ( x ) g ( x ) d x = F ( x ) g ( x ) - ∫ F ( x ) g `( x ) d x
積 分 しやすい方 を f ( x ) として 微 分 しやすい方 を g ( x ) とする
f ( x ) = e - t F ( x ) = ∫ f ( x ) d x = e - t g ( x ) = t ( z - 1 ) g ゜( x ) = ( z - 1 ) t ( z - 2 )
e (-- t) の 微 分 e (- t) t ( z- 1 ) の 微 分 ( z - 1 ) t (z - 2)
部 分 積 分 法 Youtube
積 分 の 公式集 微 分 の 公式集
------------------------------------------------------
追 記 2017 9 4 部 分 積 分 の 計 算 例
部分積分の公式 ∫ f ( x ) g ( x ) d x = F ( x ) g ( x ) - ∫ F ( x ) g `( x ) d x
問 題 - 1 ∫x ex d x
f (x) = x g (x) = e x として 計算 した 場 合
f (x) = e x g (x) = x として 計算 した 場 合
問 題 - 2 ∫x cos x d x
------------------------------------------------------
Г( z ) を ガンマ 関数 と呼ぶ[1]。この積分は、ルジャンドルの定義にしたがって、第二種 オイラー積分 とも呼ばれる。
元は階乗の一般化としてオイラーが得たもので、Γ という記号は、ルジャンドルが用いたものである。
それ以前は Π(x) などと表記していた(ただし Π(x) = Γ(x + 1))。
一般の複素数 z については、解析接続 もしくは次の 無限乗積 で定義される
ルジャンドル (フランス) 1 8 世 紀 オイラー (スイス → ロシオ)
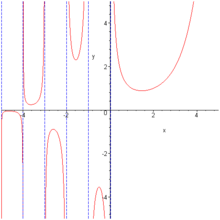
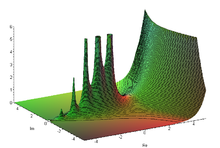
y = Γ ( x ) の グラフ Γ( x + i y ) の 絶対値 Re は に相当 I m は に 相当
y = Γ x の グラフ を 作る

テキスト に ある グラフ の 上に 計 算 結 果 を プロツト してみる
------------------------------------
いくつか の 具 体 的 な 値 [編集]
Γ( x + 1) = x Γ( x )
Γ ( - 3/2 ) = 4 √π ≒ 2.363
Γ ( - 1/2 ) = - 2 √π ≒ - 3.545
Γ ( 1/2 ) = √π = 1.772
Γ ( 1 ) = 0 ! = 1
Γ ( 3/2 ) = √π / 2 ≒ o.886
Γ ( 2 ) = 0 ! = 1
Γ ( 5/2 ) = 3 √π/4 ≒ 1.323
ガンマ 関 数 高 精 度 計 算 Yahoo
----------------------------------
階 乗 の 正 体 は ガンマ 関 数 Youtube
ガンマ 関 数 の 具 体 的 計 算 例 Γ( 3 / 2 ) = .√π / 2 とあるが
どうしても 導 出 できませんでした
Yahoo ・ Youtube では 詳しく 丁 寧 に 説 明 しているので 理 解 することができました
◆ 階 乗 の 一 般 化 Yahoo よ り
Γ・ ガンマ 関 数 の 手 計 算 に 挑 戦 し ま す
Γ( z ) = ∫0∞ t ( z - 1 ) ・ e - t d t
部 分 積 分
∫f (x) ・ g (x) d x = F (x) ・ g (x) - ∫F (x) ・ g゜(x) d x
積 分 しやすい 方 を f (x) と し 。 微 分 しやすい 方 を g (x) とするのが コ ツ
f (x) = e- t F (x) = e- t g (x) = t (x - 1) g゜(x) = (x - 1) t (x - 2)
Γ( z ) = ∫0 ∞ t ( z-1) . e - t d t = ( e-t ) t ( z-1 ) - ∫0∞ (e-t ) (z - 1) t (z - 2) d t
Γ (1) = ∫0∞ t(1 - 1) e - t d t = ∫0∞ e - t d t = 【- e-t 】0∞ = 1
Γ (2) = ∫0∞ t e - t d t = 【 - t e-t 】 o∞ + ∫0∞ e - t d t = 1
Γ (3) = ∫0∞ t2 e - t d t = 【 - t 2 e-t 】 o∞ + 2∫0∞ t e - t d t = 2
Γ (4) = ∫0∞ t3 e - t d t = 【 - t 3 e-t 】 o∞ + 3∫0∞ t2 e - t d t = 6
となる 計 算 からも 分かる ように、
Γ(4)=3!=3・2・1=6 、Γ(3)=2!=2・1=2 、Γ(2)=1!=1 、Γ(1)=0!=1
に相当していることがうかがえる。 一般に、漸化式
が成り立つので、x が自然数 n のとき、 Γ(n+1)=n! となる。
したがって、ガンマ関数は、自然数 n に対して、n!を対応させる関数(定義域は自然数
全体)を正の実数全体を定義域とする関数にまで拡張したものと考えることができる。
この意味で、 『 Γ(x+1)=x! 』 と書くことも可能ではないだろうか?
たとえば、 冒頭の (1/2)!は、
となる。 実際に、
において、
と変数変換すれば、
であるので、
となる。
(→ 参考 : 無限の拡がりをもつ面積 1 の図形について)
読者に対して、練習問題を残しておこう。
問題 (3/2)! はいくらであるか?
(追記) 当HPがいつもお世話になっているHN「攻略法」さんに解いていただきました。
(平成22年10月14日付け)
(解) (3/2)!=Γ(3/2+1)=3/2Γ(3/2)
ここで、Γ(3/2)=Γ(1/2+1)=(1/2)!=(√π)/2 なので、
(3/2)!=3(√π)/4 (終)
(コメント) 解答をお寄せいただいた攻略法さんに感謝します。
(参考文献:黒川信重 著 数学の夢 素数からのひろがり (岩波書店))
この 資 料 で ようやく ガンマ関数 が 手 計 算 できるよう になりました
◆ 以 下 Youtube
n ! = n ( n - 1 ) ( n - 2 ) ( n - 3 ) ・ ・ ・ 1
3 ! = 3 × 2 × 1 0 ! = 1
Γ (n + 1) = n !
Γ (n + 1 ) = ∫ tn e-t dt = 【 tn (- e-t) 】 - ∫0 ∞ t(n-1) (-e-t) dt
部分積分 ∫ f (x) g (x) dx = F (x) g (x) - ∫ F (x) g゜ (x) dx
Γ ( n + 1 ) = ∫0 ∞ t n ・ e-t d t ( n > 0 )
= 【 tn ( -e-t ) 】0 ∞ - ∫0 ∞ n t(n-1) ( -e-t ) d t
= 【 - tn ・ e-t 】0 ∞ + n ∫0 ∞ t(n-1) ・ e-t d t
【 - tn ・ e-t 】0 ∞ = 【-tn / et 】0∞ = -∞n / e∞ - (- 0n / eo)
lim t→∞ -tn / et = lim t→∞ o / et = o / ∞ = o
Γ ( n + 1 ) = ∫0 ∞ tn e-t dt = n ∫0 ∞ tn e-t dt = n Γ ( n )
Γ (n + 1 ) = n Γ ( n ) = n ×( n - 1 ) Γ ( n - 1 )
= n × ( n - 1 ) × ( n - 2 ) Γ ( n - 2 )
= n × ( n - 1 ) ×( n - 2 ) ×・・・ × 1 Γ ( 1 ) = n !
Г ( 0 + 1 ) = Г ( 1 ) = 0 ! = 1
( 1 / 2 ) ! = Γ( 3 / 2 ) = ∫0 ∞ t ( 1/2) e- t dt = ∫0 ∞ √t e- t dt
= 【 - √t e-t dt 】 - ∫0 ∞ ( - 1 / 2 √t ) e-t
= 【 - √t e-t dt 】 + ∫0 ∞ ( 1 / 2 √t ) e-t
x = t1/2 dx / dt = (1/2) t-1/2 = 1 / 2 √t
dx = dt / 2 √t
( 1 / 2 ) ! = ∫0 ∞ e-x2 dx
I = ∫-∞ ∞ e-x2 dx × I = ∫-∞ ∞ e-y2 dy
I 2 = ∫-∞ ∞ ∫-∞ ∞ e-(x2 + y2) dxdy = π
I = √π
x = r cosθ y = r sinθ x2 + y2 = r2
∂ r cos θ/ ∂θ ∂ r cos θ/ ∂θ cos θ - r sin θ
行列式 = r cos2 θ + r sin2 θ = r
∂ r sin θ/ ∂ r ∂ r sin θ / ∂ r sin θ r cos θ
I 2 = ∫-∞ ∞ ∫-∞ ∞ e-(x2 + y2) dxdy = ∫02π ∫0∞ e-r2 r d r dθ
= ∫02π 【 (- 1/2 ) e-r2 】 0∞ dθ
= ∫02π (1/2 ) d θ = 【 (1/2) θ】02π = π I = √π
(1/2) ! = (√π) / 2
ー ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ガンマ 関 数 の 勉 強 を 始 め た 時 資 料 の 冒 頭 に
【 ガンマ 関 数 は 階 乗 の 概 念 を 一 般 化 し た 特 殊 関 数 で あ る 】 と あ り ま し た
全 般 が ほぼ 理 解 できた 今 この 意 味 が分かりました 欲 求 不 満 解 消
尚 ベツセル 関 数 ベータ 関 数 等 は ガンマ 関 数 の 延 長 線 にあるので 親 し み やすくなりました
------------------------------------ーーーーーーー
◆ Γ ガンマ 関 数 は いろんな 関 数 式 に 現 れ る
他 の 特 殊 関 数 も ガンマ 関 数 の 線 上 にあるものが多 く 親 しみ やしくなりました
ベッセル 関 数
Jα (x) = (-1)m / 【 m! ( Γ( m + α+ 1 ) ) 】 (x/2)2m+α
β 関 数 と Γ関 数 の 関 係
B ( x 、y ) = 【 Γ(x) Γ(y) 】 / Γ( x + y )
ワイブル 分 布
確率分布 より その 密度関数 は 【 【 Γ( n/2 + 1/2 ) 】 / 【 (√nπ) Γn/2 】 】 【 1 + x2 / n 】- (n+1)/2
------------------------------------
● ベ ツ セ ル 関 数


ベルヌーイ ( スイス ) 18世紀 ベツセル ( ドイツ )
ダニエル・ベルヌーイ は 13 歳 で 大 学 15 歳 で 学士試験合格 16 歳 で 修士号 取 得
父 兄 弟 本人 皆 学 者
ベッセル関数 Bessel function とは、最初にスイスの数学者 ダニエル・ベルヌーイ によって定義され、
フリードリヒ・ヴィルヘルム・ベッセルにちなんで名づけられた関数。 円 筒 関 数 と呼ばれる。
以下に示す、ベッセルの 微分方程式 におけるの 特殊解 の1つである
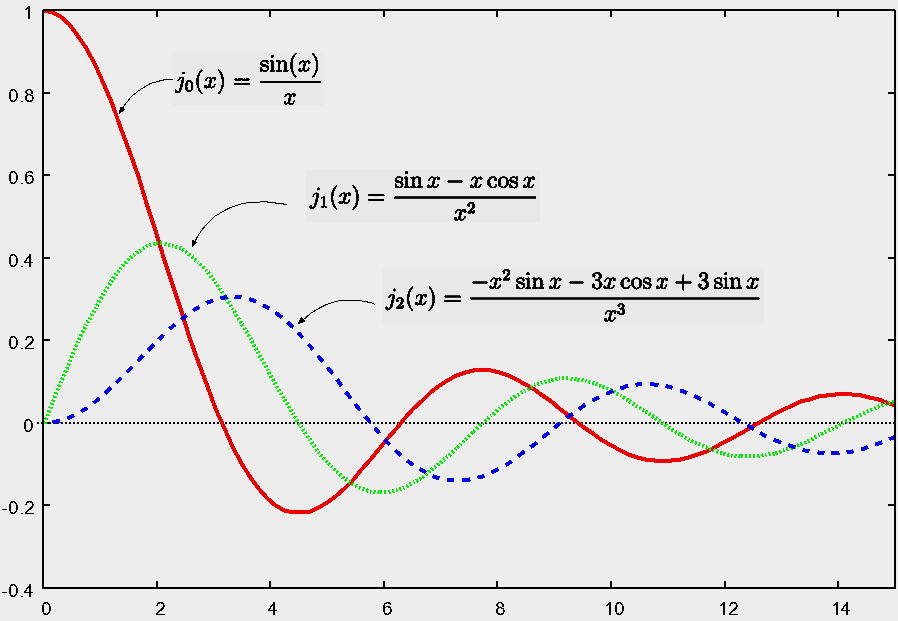
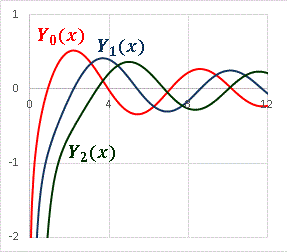
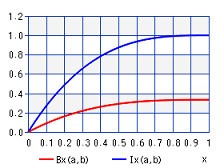
第 1 種 ベツセル関数 グラフ 第 2 種 ベツセル関数 グラフ
第Ⅰ種 ベツセル 関 数 グラフ 高 精 度 計 算 CASIO
Bessel function of the 1st kind Jν ( x )
( 1 ) x 2 y" + x y´ + ( x 2 - ν2 ) y = o y = Jν ( x )
( 1 ) Jν ( x ) = Σk=0 ∞ 【 (-1 ) k / k !Γ( k + ν+ 1 ) 】 ( x / 2) ν+ 2k
( 1 ) e ( x / 2 ) ( t - 1 / t ) = Σk=0 ∞ 【 Jn ( x ) tn n = integer
第2種 ベツセル 関 数 グラフ 高 精 度 計 算
Bessel function of the 2nd kind Yν ( x )
( 1 ) x 2 y" + x y´ + ( x 2 - ν2 ) y = o y = Yν ( x )
( 1 ) Yν ( x ) = Jν ( x ) cos ( νπ) - J-ν ( x )
( 1 ) Y-ν ( x ) = (- 1)n Yn ( x )
▲ 第 1 種 ベツセル 関 数
第 1 種 ベッセル 関 数 は Jα ( x ) と 表 記 される。
Jα ( x ) はベッセルの微分方程式の解であり、α が整数もしくは非負であるとき、 x = 0で有限の値をとる
。 Jα における、特定解の選択及び正規化は定義された後に、後述する。
第1種ベッセル関数はまた、x = 0 のまわりでの テイラー展開 (非整数の α に対しては、
より一般に べき級数展開 によって定義することもできる。
非整数の α に対しては、 Jα ( x ) と J -α ( x ) とが、ベッセルの微分方程式に対する線形独立な2つの解を
与える。整数の に対してはこれらは線形独立な解を与えない。
なぜなら、整数 に対して、 Jα ( x ) と J -α ( x ) と の あいだには 関 係
が成り立ち、両者は明らかに 線形従属 となるからである。
整数次数に対して Jα ( x ) と 線形独立な第二の解 は、以下の第2種ベッセル関数によって与えられる
▲ 第 2 種 ベツセル 関 数
第 2 種 ベッセル 関 数は Y α ( x ) と 表 記 される
Y α ( x ) はやはり ベッセルの微分方程式の解 であり、
x = 0 において特異性をもつ。また、Y α ( x ) は、しばしばノイマン関数とも呼ばれ、N α ( x ) とも表記される。
第1種 ベッセル関数 J α ( x ) との関係 は
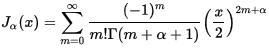
- で与えられる。ただし、α が 整 数 のときは 右 辺 は 極 限 によって 定 義 されるものとする。
- 非整数 の α に対しては、 J α ( x ) と J -α ( x ) とが 線形独立 な 2 つ の 解 をすでに与えているので、
- Y α ( x ) は 解 の表現としては冗長である。
- 整 数 n に対しては、はと 線形独立な第二の解 を与えている。
- 整 数 n に対して、Y α ( x ) と Y - α ( x ) とのあいだには 関 係
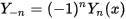
が 成り立ち、したがって両者は やはり 線 形 従 属 である。- J α (x ) 及び はどちらも、負の実軸を除く複素平面上で x の解析的な関数(正則な関数)である。
-
- また、固 定 した x に対して、ベッセル 関 数 α の 整 関 数
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
● ベーター 関 数
ベータ 関 数 beta function) と は
、ルシャンドル の 定 義 に従って 第一種オイラー積分 とも呼ばれる 特 殊 関 数 である
β 関 数 高 精 度 計 算
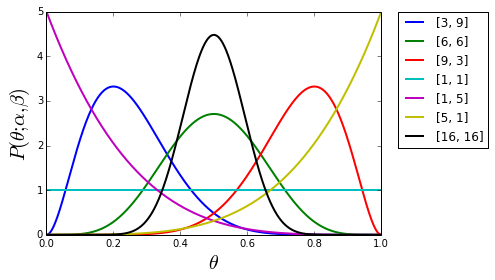
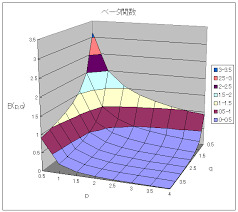
B ( x , y ) = ∫ o1 tx-1 (1 - t) y-1 d t
変 数 変 換 した 積 分 表 示
B ( x 、 y ) = 2 ∫ 0π/2 sin2x-1 θ cos2y-1θ dθ
B ( x 、 y ) = 2 ∫ 0π/2 tx-1 / 【 (t + 1)x + y 】 d t
B ( x 、 y ) = 1 / 2x + y -1 ∫-11 (1 + t)x-1(1-t)y-1 d t
ベータ 関 数 との 関 係
ベータ 関 数 は 次 の よ う に ガンマ 関 数 と 結 び つ く
B ( x ・y ) = 【 Γ(x) Γ(y) 】 / Γ (x + y)
例 x = 1 y = 2 答 え 0.5
手 計 算 B ( 1 ・2 ) = 【 Γ (1) Γ(2) 】 / Γ(1 + 2) = 1/2 = 0.5
ガンマ 関 数 を 使つうて 計 算
次 は 積 分 を 使つて 計 算
B ( 1 ・2 ) = ∫01 ta-1 (1-t)b-1 d t
= ∫01 t1-1 (1-t)2-1 d t = ∫01 t0 (1-t)1 d t
= ∫01 (1-t) d t = 1/2 = 0.5
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
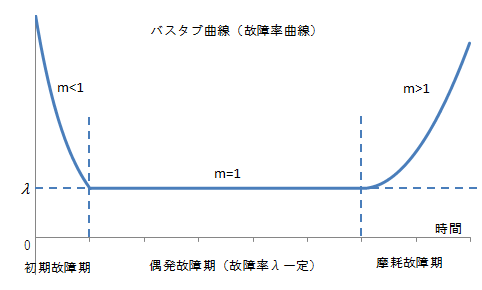
★ 信 頼 性 関 係
会 社 が 職 場 名 お 信 頼 性 管 理 部 と 名 付 け てくれました
信 頼 性 の 勉 強 お し ま し た
信 頼 性 工 学 ( 耐 久 試 験 途 中 打 ち 切 り 試 験 加 速 試 験 ) FMEA FTA TQC 等
業 務 に 役 立 っ た 例
① いすゞ 納 め の モトロイド
いすゞ 設 計 は 今 度 の 新 車 は 耐 久 性 の 信 頼 性 は シックス ナイン 99.9999 と うそぶいておりました
私 た ち は 30 個 の 試 作 品 お 回 数 打 ち 切 り 法 で 耐 久 性 試 験 お 行 い ました
試 験 結 果 を 解 析 したところ 信 頼 性 は フォー ナイン 99、99 でした
この 結果 を いすず 設 計 に 報 告 したところ こういゅう 耐 久 性 確 認 をしてくれると よい といって ほめてくれました
どのように 解 析 するのか 質 問 がありました ので 私の 使った 信 頼 性 工 学 の 参 考 書 を 紹 介 しておきました
② マツダ 納 め の 電 磁 ブ ン ブ
納 入 開 始 後 しばらくして 何 個 かの 市 場不 良 品 が 回 収 されてきました
日 立 経 由 で 納入していました 日 立 は 全 数 回 収 交 換 すべきだと いってきました
不 良 品 を 調 査 したところ 基 盤 に 切 り 粉 が 付 着 していて それによる 電 食 マイグレーション と分かりました
また、 不 良 品 の 情 報 回 収 数 発 生 時 期 等 より ワイブルチャート での 解 析 結 果
不良 モード は 初 期 不 良 そして 今 後 の 発 生 個 数 は ひと 桁 に とどまることが 分かりました
筒 井 さん と マツダ に 報 告 にいきました
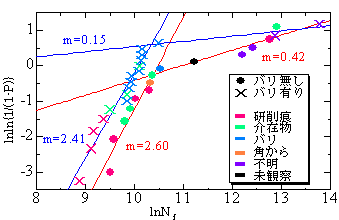
私 の レボート を 保 存 し て お け ば よ か っ た
マ ツ ダ 設 計 の 方 は ワイブルチャート 解 析 がよく分からなかったようで 統 計 班 の 方 を 呼 び ました
統 計 班 の 方 は 納 得 してくれました
全 数 回 収 交 換 が 避けられた の で ホット しました
③ 加 速 試 験 ウォッシャー ブ ン ブ
ウォッシャー ブ ン ブ は 短 時 間 使 用 短 時 間 定 格
耐 久 時 間 をなるべく 短 く したい
-
耐 久 中 の 温 度 上 昇 を 50 度 にしたとき ブンブ 作 動 の ON - OFF Duty を どう きめたらよいか
◆ まず ウォッシャー ブ ン ブ を 連 続 作 動 させたときの 温 度 上 昇 を 測 定 する
温 度 上 昇 曲 線 より 時 定 数 τ を 算 出 する
◆ 充 放 電 回 路 50 度 C になるように 時 定 数 を 使って Duty を 算 出 する
④ ク レーム 品 調 査 の 思 い 出
◆ ワイバー モーター 間 欠 ア ン ブ 故 障
新 型 アンブ 間 欠 を 新 車 に 取 り 付 け て もらいました
新 車 発 表 の 展 示 会 場 よ り つぎつぎ と 間 欠 アンブ の 不 良 情 報 が 入って きました
不 良 品 を 調 査 してみると Can タイブ IC 内 の ダイオード が 破 損 しておりました
客 先 工 場 の 片 隅 に 新 車 を 3 台 借 り て 再 現 テスト 調 べ ました
なかなか 再 現 しないので 3 日 通 い ました
3 日 目 には 平 野 社 長 が 富音工場 出 張 の 帰り道 立ち寄って くれました じっと 眺 め て おりました
ウオッシャーブンブのスイッチを切ったり 入れたり 繰り返していたら ある時 ブラウン菅に
異 常 波 形 が 現れました アンブ は 破 損 しておりました アンブ 破 損 が 再 現 できました
原 因 は ウォッシャーブンブ モーター から 発 生 する ノイズ 異 常 バルス で ダイオード が 破 損 しました
ウォッシャー スイッチ を チョン 押 し すると ブンブ モーター が 廻 り 始める 前 に 起動電流 の 大きい 時 に
スイッチ が 切られるので 発 生 ノイズ バルス が 大 き い ことでした
この発生バルスを吸収するためにコンデンサー 1 個 追加したら IC 故障破損はなくなりました
社 長 はだまって 帰 っ て いきました
ホット 安 心 したら どっと 疲 れ がでました
翌 朝 疲 れ で 起 られませんでした 秘 書 室 から 電 話 があり 社 長 が 出てこい とのこと
社長は 工場長 はじめ 関係者 を 集めて 対 策 会議 を もってくれました
後 で 反 省
実 は 、 私 が 回 路 設計者 に I c 内 に ダイオード が 遊 ん で いる これを 使 え ば 外 付 け ダイオード が
節 約 できるよ と 話 ま し た 若 い 設 計 者 は 鵜 呑 み に 採 用 しました
設計者 も 私 し も I c 内 の ダイオード の 耐 圧 耐 電 流 容 量 を 考えて いませんでした
私 は 責 任 を 感 じ て 社 長 他 役員一同 宛 て に 身 退 伺 い 書 を 秘 書 室 を 通して 出 し ました
後 で 秘 書 室 長 に 聞 い た ら 社 長 は ボケット に 入れて 家 に 持 ち 帰 っ た と 言って おりました
◆ ワイバー モーター キャーケース 破 損
ワイバ モーター の 市 場 クレーム 品 が 沢 山 回 収 されてきました
ギャーケース の 出 力 軸 受 の 根 本 から ボックリ も ぎ 取 っ た ように 破 損 しておりました
設計課長 と 相 談 して 対 策 は 出 力 軸 の 根 本 の 集 中 応 力 を に 耐えられる ように
軸 受 の 根 本 に R を つけること にしました
対 策 品 と 従 来 品 の 破 壊 強 度 試 験 を して 比 較 す ると 当 然 大 幅 に 強 度 Up しておりました
その後 市 場 クレーム はなくなりました
◆ 水ブンブ ゴムホース 間 の T 型 樹 脂 コネクター 破 損
H L C ( ヘッド ランプ クリーナー )
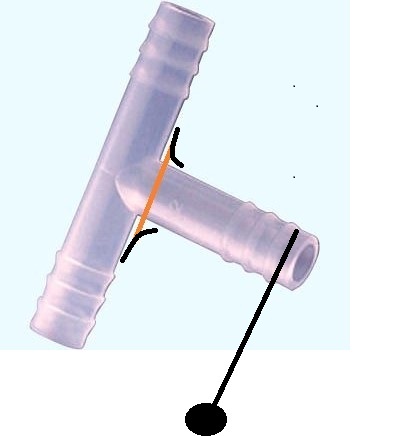
ボンブ は ゴム ホース を 繋 い で T 型 コネクター で 分 岐 し て 2 方 向 に 分けて おります
納 入 時 の 荷 姿 は ボンブ に ゴ ム ホース を かるく 巻 き 付 け て バレット に 入れて 輸 送 します
客 先 から バレット か ら ボンブ を 取 り 出 す と 何 個 か T 型 コネクター が 破 損 している
と の 情 報 が 入 り ました
ク ケーム 品 を 見 る と 上 図 赤 線 の 部 分 が カミソリ で 切 っ た ように 破 損 しておりました
再 現 試 験
作 業 台 に T 型 コネクター を 固 定 して 紐 に 20 グラム 程 度 の おもり を ぶら 下 げ ました
翌 朝 出 社 してみると クムーム 品 と 同 じ ように みごとに カミソリ で 切 っ た ように 破 損 しておりました
破 損 原 因 は 納 入 荷 姿 で ボンブ に ゴム ホース を 巻 き 付 け て いたのでT 型 コネクター は いつも 引 っ 張 ら れ ている
樹 脂 分 子 の 架 橋 が ほずれて い き やがて 破 損 する ことでした
対 策 は 上 図 のように 根 元 に R を つけました
その後 クケーム はなくなりました
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
● 確 率 密 度 関 数 ( P D F Probabirity Density Function )
P r 【 a ≦ X ≦ b 】 = ∫ab f (x) d x
ガ ウ ス 積 分 ( オイラー = ポアソン積分 ) が Base
∫-∞∞ e -x2 d x = √π
① 二 重 積 分 を 用 い る 方 法 Yahoo ∫-∞∞ e (-x2) d x
I = ∫-∞∞ e (-x2) d x とすると I = ∫-∞∞ e (-y2) d y でもる
I 2 = ∫-∞∞ ∫-∞∞ e (-x2-y2) dx dy x = r cos θ y = r sin θ
= ∫02π ∫-∞∞ e (-r2cos2θ-r2sin2θ) dr dθ
(-r2cos2θ-r2sin2θ) = (-r2)
= ∫02π ∫-∞∞ r e-r2 dr dθ =∫02π (1/2) dθ = π
√( I2 ) =∫-∞∞ e (-x2) d x = √π
② 重 積 分 によらない 技 巧 的 な 方 法
f (t) = 〔∫01 e-x2 dx 〕2 g (t) = ∫01 〔 e -t2 ( 1 + y2 ) 〕 / (1 + y2)
f ゜(t) = 2 e -t2 ∫01 e-x2 dx =
.png)
確 率 論 統 計 論 物 理 学 等 で 重 要 と い う
-------------------------------
確 率 密 度 関 数
f (x) = 1 / √2πσ2 ・ e 【 - ( x - μ)2 】
μ ← 平 均 値 σ2 ← 分 散
標 準 正 規 分 布 上式 に おいて 特 に μ= 0 σ2 = 1 の 場 合
f (x) = 1 / √(2π) e ( - x2 / 2 )
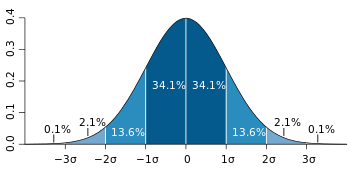
正 規 分 布
f ( x : μ , σ2 :) = 【 1 / √( 2πσ ) 】 ・ e ( - 1/2 ) 【 ( x - μ ) / σ 】 2 】
μ = 平 均 値 σ2 = 分 散
正 規 分 布 ( グ ラ フ ) 高 精 度 計 算
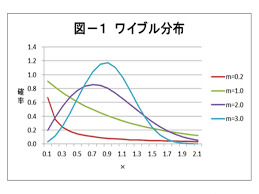
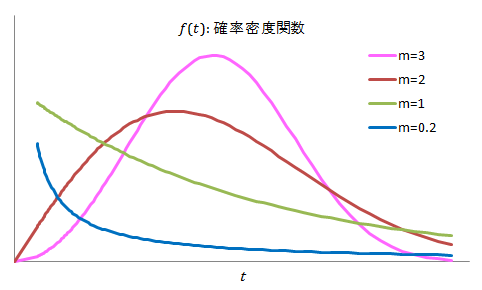
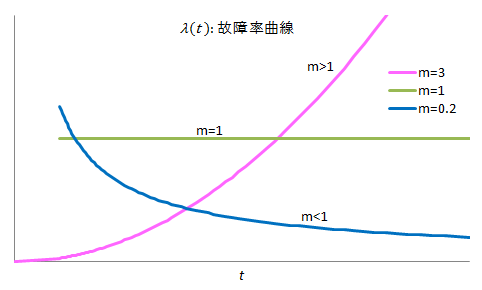
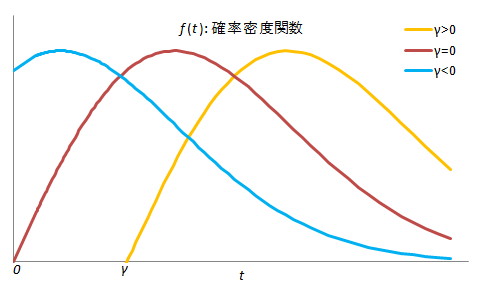
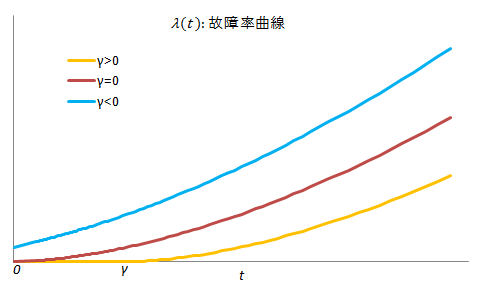
ワ イ ブ ル 分 布
私 は ワイブル 分 布 ワイブル チャート は 業 務 上 必 要 だつた ので 力 ず く で 暗 記 しました
f (t) = ( m / η ) ( t / η ) m-1 exp 【 - ( t / η ) m 】
m は ワイブル 係 数 ( 形 状 バラメータ ) η は 尺 度 バラメータ
μ = η Γ ( 1 + 1/m )

ワイブル 分 布 ( グ ラ フ ) 高 精 度 計 算

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
分からない 数 学 問 題 も しつこく 食らいつて いると 少しじつ 分かつて くるものです
あきらめない ことですね
こ の べーじ の Top へ
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
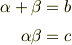
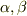 は
は 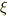 の2次方程式
の2次方程式