np - 200　　　　　　　　　

　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー


　　　　　　　


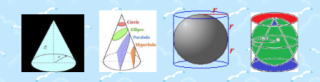
　　　　　　　　円 筒 に 内 接 する 球 と 円 錐 において 面 白 い 関 係 を 発 見 しました　


　　　　　　　　　　　　　　　　　体 積　 と 　表 面 積　の　公 式　

　　　　　　　　　　　　円 錐　　　　　V = (1/3) S h = (2/3) πr³　　　　　S = ( 1 + .√5 ) πr²

　　　　　　　　　　　　 球　　　　　　V = (4/3) πr³ 　　　　　　　　　　　 　S = 4 πr²

　　　　　　　　　　　　円 筒　 　　　 V = 2 πr³　　　　　　　　　　　　　　　 S = 6 πr²


　　　　　　　　●　　　体 積 比　　　　円 錐　_“　球　_“　円 筒　= 　1_“　2_“　3

　　　　　　　　【 (2/3) πr³ 】　_“ 【 (4/3) πr³】 _“　【 2 πr³ 】 = (2/3) _“　(4/3) _“　2　= 1　２　3

　　　　　　　　　　　　　　　　　　　　きれいな　体 積 比　です


　　　　　　　　●　　　体 積 と 表 面 積 の 公 式　　　　　　大 発 見

　　　　　　　　　　“　体 積 の 公 式 を 微 分 すると 表 面 積 の 公 式 となる　“

　　　　　　　円 錐　　　　dV / dr = 【 (2/3) πr³　】 ゜ = 2 πr² 　≠ 　S = ( 1 + .√5 ) πr²


　　　　　　　　　　　　　球　　　　　dV/ dr = 【 (4/3) πr³】 ゜ = 4 πr² 　= 　S

　　　　　　　　　　　　円 筒　　　　dV / dr = 【 2 πr³】 ゜ = 6 πr² 　=　 S

　　　　　　　　さらに　“　表 面 積 の 公 式　を 積 分 すると 体 積 の 公 式　となる　“

　　　　　　　　　　　　円 錐　　　　∫S dr = ∫₀ ^r 2 πr² dr = (2/3) πr³ 　= 　V

　　　　　　　　　　　　　　　 　　球　　　　　∫S dr = ∫₀ ^r 4 π r²dr = (4/3)πr³ 　=　 V

　　　　　　　　　　　　円 筒　　　　∫S dr = ∫₀ ^r 6 πr² dr = 2 πr³ 　=　 V


　　　さらに　“　円筒 の 側 面 積 の 公 式　を 積 分 すると 内接球 の 体 積 の 公 式　となる
　
　　　　　　　　　　　　　∫S_h dr = ∫₀ ^r　4π r² dr = (4/3) π r³ 　= 　V


　　　　　　　　驚 きました　体 積 と 表 面 積 の 公 式 が 微 分 と 積 分 で 導 かれるとは　

　　　　　　　　　　　この　発　見　は　公 式 を 並べて 眺 めて いる中 に 気 づ き ました


　　　　　　　　　摩 訶 不 思 議　ひとり　悦 に 入っております　


　　　　　　　　　　　　　　　　　　　こ の　ページ　 の　Top　へ