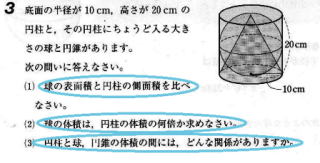
媴 偺 昞柺愊 偲 懱 愊
丂丂s - 31
H 25 05 07 Up
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂俀侽侾俉丂侾丂侾俇丂丂俬値倫倳倲丂俿倕倱倲
丂丂丂壣偮傇偟 偺 悢妛 偍梀傃丄拞妛丂崅峑帪戙 偺 悢妛 偺 暅 廞 傕傑偨妝 偟偄丅丂丂摢 偺 懱憖丂擣抦徢 梊 杊
丂丂丂丂丂丂丂媴 偺 柺 愊 偲 懱 愊 傪媮傔傞偺偼愭偵 懱 愊 傪媮傔傞曽朄 傪 棟 夝偡傞 偺偑傛偝偦偆偱偡丅
仛丂 丂丂 媴 丂丂丂偺 丂懱 愊丂 偺 媮 傔 曽 丂丂
丂丂丂丂丂丂丂丂丂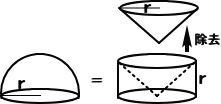 丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂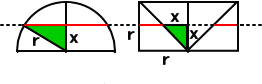
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂-丂1丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂亅丂2
丂丂丂丂恾 - 1 敿 媴 偺懱愊丄墌 拰 偺懱愊丄墌拰偐傜 墌悕 傪愗傝庢偭偨 懱愊丄偲 墌 悕 偺懱 愊傪 斾 妑 偟傑偡
丂丂丂丂丂仭丂丂敿 媴 偺 懱 愊丂 = 丂(2/3) 兾 r3丂丂丂丂媴 偺 懱 愊丂偼丂2 攞 偺丂丂丂(4/3) 兾 r3
丂丂丂丂丂丂丂恾 - 2丂偱 帵 偡 傛偆偵丄丂掙 柺 傛傝 崅 偝丂x 偺 抐 柺 偺 墌 偺 柺 愊 偼丂丂兾 ( r2 - x2 )
丂丂丂丂丂丂丂丂丂丂丂丂丂丂廬偭偰丄丂敿 媴 偺 懱 愊丂偼 愊 暘 偟偰
丂
丂丂丂丂丂丂丂丂丂丂丂V= 丂佺0 r丂兾 ( r2 - x2 ) dx = 兾乲 r2 x - (1/3) x3 乴 0 r
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂= 兾 r3 - (1/3) 兾 r3 丂=丂 (2/3) 兾 r3
丂丂丂丂丂丂丂丂丂媴丂偼丂丂2丂攞 偟 偰丂丂 丂(4/3) 兾 r3丂丂 丂丂( 恎 偵 怱 攝 偁傞偺偱 嶲 忋 )丂丂偲 妎 偊 傞
丂丂丂丂丂仭丂丂墌 拰 偺 懱 愊 = 掙 柺 愊丂亊丂崅 偝丂= 兾 r2 亊 r = 兾 r3
丂丂丂丂丂仭丂丂墌 拰 偐傜 墌悕 傪愗傝庢偭偨懱 愊 = 兾 r3 - (1/3) 兾 r3 = 丂(2/3) 兾 r3 丂= 敿 媴 偺 懱 愊
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂僈僶儕僄 偺 掕 棟
丂丂丂丂丂丂丂丂丂丂俀 偭 偺 棫 懱 傪丄暯 峴 側 暯 柺 偱愗偭偨偲偒偺 愗丂傝丂岥丂偺 柺 愊 偑偄偮傕 摍偟偗傟偽丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俀 偭 偺 棫 懱 偺 懱 愊 偼 摍偟偄丅
丂丂丂丂丂丂丂丂丂丂恾 - 2丂偱丂敿 媴 偺 愒 慄 偺 抐柺愊 偲 墌 拰 偺 愒 慄 偺 抐 柺 愊 偼偲傕偵丄丂兾 ( r2 - x2 )
丂丂丂丂丂仭丂丂墌 悕 偺 懱 愊丂 =丂 (1/3) 兾 r3丂丂丂丂丂丂丂丂丂( 徻 嵶 愢 柧丂徹 柧 偼丂屻 偱 )
仛 丂 丂悕 懱 丂丂偺 丂丂懱 愊丂丂V 掙 柺 愊 偑 S丂崅偝 偑 h 偺偲偒丂V = (1/3) S h丂偱偁傞偙偲偺 徹 柧丂
丂丂丂丂丂丂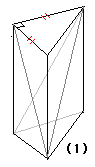 丂丂丂
丂丂丂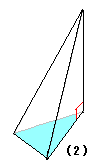 丂丂丂丂
丂丂丂丂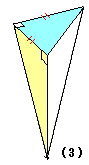 丂丂丂丂
丂丂丂丂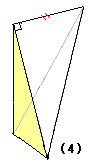 丂丂丂丂
丂丂丂丂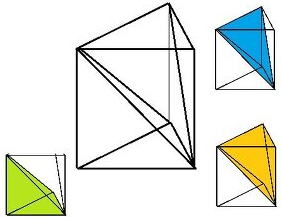
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(1) 偼 掙 柺 愊丂S丂崅 偝丂h丂偺 3 妏 拰
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偺 3 妏 拰 偼丂(2)丂 (3)丂 (4)丂偺丂3 屄丂3 妏 悗
丂丂丂丂丂丂丂丂丂丂丂丂3 妏 拰丂偺丂懱 愊 偼丂丂丂V = S h 丂丂丂3 妏 悕 偺 懱 愊 偼 丂丂V3 = (1 / 3) S h
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂妛 栤 揑 偵偼 僈僶儕僄 偺 掕 棟 偑偁傝傑偡
丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂亂僇償傽儕僄儕 偺 尨 棟 亃丂丂Wikipedia丂傛傝丂堦晹 傪 僐 僺乕
丂丂丂丂丂丂丂丂丂僇償傽儕僄儕 偺 尨 棟 乮僇償傽儕僄儕偺偘傫傝丄Cavalieri's principle乯 偼丄柺 愊 傗 懱 愊 偵 娭偡傞
丂丂丂丂丂丂丂丂堦斒揑側 朄 懃 偺傂偲偮偱偁傞丅僇償傽儕僄儕 偺 掕 棟丄晄壜暘偺曽朄 (method of indivisibles)
丂丂丂丂丂丂丂丂椺偊偽 懱 愊 偵偮偄偰偺 僇償傽儕僄儕 偺 尨 棟 偲偼丄戝傑偐偵偼丂 乽愗傝岥偺柺愊偑忢偵摍偟偄2偮偺
丂丂丂丂丂丂丂丂棫懱偺懱愊偼摍偟偄乿偲偄偆 庡 挘 偱偁傞丅丂丂丂僇償傽儕僄儕 偼 17悽婭 偺僀僞儕傾 偺 悢 妛 幰丅
丂
仛丂丂丂墌 悕丂丂偺丂懱 愊丂偺 媮傔 曽
丂丂丂丂丂丂丂丂丂丂丂丂丂丂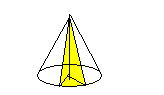 丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂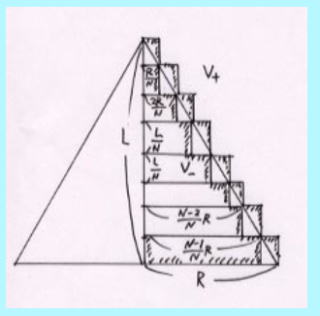
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾乕侾丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾乕2
丂丂丂丂丂丂
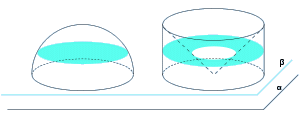
丂丂丂丂丂仭丂丂恾丂- 1丂傪巊偭偰丄 墌 悕 偺 懱 愊 傪 媮傔傞丂
丂丂丂丂丂丂丂丂丂丂丂丂悕 懱偺懱 愊 偼丂掙柺愊丂S丂崅偝丂h丂偲偡傞偲丂V = (1/3) S h 丂偱偁傞偙偲偼 愢 柧 嵪 偱偡
丂丂丂丂丂丂丂丂丂丂丂丂丂恾乕1丂偺 墌 悕 偵 墿怓 偺 愵忬悗 傪 10屄 堦 攖 偵 媗 傔 偨偲壖掕偟傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂愵忬悗 偺 掙 柺 偼 2 曈 偑丂r丂 墌 屖 偑丂兤 = (2 兾 r) / 10
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂廬偭偰 掙柺愊 偼丂丂S3 =丂 (1/2) r2 兤丂=丂(1/2) r2 (2兾/10) = 兾r2 / 10丂偲側傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂寢嬊丄愵忬悗丂10 屄丂媗傔偨偺偩偐傜丂S3丂亊丂10 = ( / 10) 10 = 兾r2 = S
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂V = (1/3) S h
丂丂丂丂丂丂仭丂丂恾丂- 俀丂傪巊偭偰丄丂嬫 暘 媮 愊丂偱 媮傔傞
丂丂丂丂丂丂丂丂丂丂丂丂丂墌 悕 偺 懱 愊丂傪媮傔傞偨傔偵丄偙傟偵撪愙偡傞偦傟偧傟偺丂崅偝丂L / N丂偺丂N - 1 屄丂偺
丂丂丂丂丂丂丂丂丂丂丂丂丂墌 拰 偵 暘 妱 偟偰 懱 愊丂傪嬤 帡 揑 偵媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偙偱丄丂N = 10丂偲偡傞偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂Vin = (L/10)兾 (R/10) 2 + (L/10) 兾 (2 R/10) 2 +丒丒丒丒+ (L/10) 兾 (9 R/10) 2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = (L/10) 兾 (R/10) 2 ( 1 + 22 + 32 + 丒丒丒丒 + 92 )
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = (1/103) 兾 R 2 285 丂佮 丂0.29 L 兾 R 2 =0.29 SL 佮 (1/3) S L
丂丂丂丂丂丂丂丂丂丂丂丂丂摨 條 偵丄奜 愙偡傞 墌 拰 偵 暘 妱 偟偰 懱 愊丂傪 嬤 帡 揑 偵媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂Vout = (L/10)兾 (R/10) 2 + (L/10) 兾 (2 R/10) 2 +丒丒丒丒+ (L/10) 兾R 2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂= (L/10) 兾 (R/10) 2 ( 1 + 22 + 32 + 丒丒丒丒 + 102 )
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂= 丂(1/103) L 兾 R 2 385 丂佮 丂0.39 L 兾 R 2 =0.39 S L 佮 (1/3) S L
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(Vin丂+丂Vout) / 2 = ( 0.29 + 0.38 ) / 2 佮 0.34佮 1 / 3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂N 丂傪丂亣丂偵偡傟偽丂丂丂丂V = (1/3) S h丂丂偵丂廂 懇丂偡傞
丂丂丂丂丂仭丂丂愊 暘丂偱丂媮 傔 傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂掕 愊 暘 偲 懱 愊
丂丂丂丂丂丂丂丂丂丂丂丂嵗昗嬻娫拞偺丄 a丂亝 z 亝 b丂偺斖埻偵抲偐傟偨棫懱恾宍傪 x y 暯柺偵暯峴側暯柺 z = t 偱
丂丂丂丂丂丂丂丂丂丂丂愗抐 偟偨偲偒偺 抐 柺 愊 丂S (t) 偲偡傞偲丄偙偺棫懱恾宍偺 懱 愊 偼丄丂丂V = 佺a b S (z) dz
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂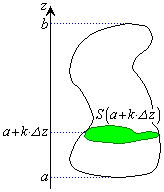
丂丂丂丂丂丂丂丂丂 a丂亝 z 亝 b丂偺斖埻傪n 摍 暘 偟丄嚈z = (b - a) / n 丆 k = 1丄 2丄 3 丒丒丒 丒n 偲偟偰丄暯柺 z
= a + k 丒嚈z 偱
丂丂丂丂丂丂丂丂丂棫 懱 恾 宍 傪 愗 抐丂偟偨偲偒偺丂抐 柺 愊 偼丂丂S (a + k 嚈z) 丂偱偡丅
丂丂丂丂丂丂丂丂丂偙偺偲偒偺 愗 抐 柺 傪 掙 柺 偲偟丄崅 偝嚈z 偺 拰 懱 Pk 傪峫偊傞偲丄Pk 偺懱 愊 偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S (a + k 嚈z)丂丂偱 梌偊傜傟傑偡丅
丂丂丂丂丂丂丂丂丂P1丄 P2 丒丒丒丒丂Pn 偺 懱 愊 偺憤 榓 丗 偼丄偺 嬌 尷 偱 棫 懱 偺 懱 愊丂V 丂偵 嬤偯偒傑偡丅
丂丂丂丂丂丂丂丂丂傛偭偰丄嬫暘媮愊朄 偵傛傝丄丂V = limn仺亣 儼k=1 n S (a + k 嚈z) 嚈z = V = 佺a b S (x) dx
丂丂丂丂丂丂丂丂椺丂1丏丂敿 宎r 丂偺 墌 傪 掙 柺 偲偟丄崅 偝丂h丂偺墌 悕 偺 懱 愊 傪媮 傔傞丅
丂丂丂丂丂丂丂丂[夝摎]丂丂丂掙 柺 偺墌 偑 x y 暯 柺 忋 偵 抲 偐 傟 偰偄傞偲偟偰峫偊傑偡丅
丂丂丂丂丂丂丂丂暯 柺 丂z = t 偱 墌 悕 傪愗偭偨偲偒偺 抐 柺 偺 墌 偺 敿 宎 傪 r 丩 偲偟偰丄r 丗r 丩 =
h 丗 (h - t)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亪丂r 丩 = 亂 (h - t) / h 亃 r
丂丂丂丂丂丂丂丂丂抐 柺 偺 墌 偺 柺 愊 偼丄丂丂S (t) = 兾 亂 (h - t) / h 亃2 r 2
丂丂丂丂丂丂丂丂傛偭偰丄墌 悕 偺懱 愊 偼丄丂丂V = 佺0 k 丂S (z) dz= 佺0 k 兾 亂 (h - z) / h 亃2 r 2 dz
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = 亂 (兾 r2) / h2 亃 佺0 k (h2 - 2 h z + z2) dz
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = 亂 (兾 r2) / h2 亃 亂h2z - hz2 + (1/3) z3亃0 k
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = 亂 (兾 r2) / h2 亃 亂h3 - h3 + (1/3) h3 亃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = 丂丂丂(1/3)丂兾 r2 h
丂丂
丂丂丂丂丂丂丂丂墌 悕 偵尷傜偢丄掙柺愊S 丆崅偝 h 偺 悕 懱 偱偼丄 暯柺 z = t 偱 愗 抐 偟偨偲偒偺 抐 柺 愊 偑
丂丂丂丂丂丂丂丂亂 (h - t) / h 亃2 S丂偱梌偊傜傟傞偺偱丄忋婰偲摨 偠傛偆偵 愊 暘 偟偰丄悕 懱 偺 懱 愊丂偼丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂V 丂=丂 (1/3) 兾 r 2丂h = (1/3)丂 S丂h丂丂側傝傑偡丅
仛丂丂丂 媴丂 丂偺 丂昞柺 愊 丂偺 媮 傔 曽
丂丂丂丂丂丂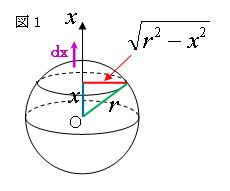 丂丂丂
丂丂丂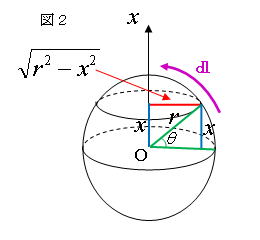 丂丂丂丂
丂丂丂丂 丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂-丂1丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂-丂2丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂-丂3
丂丂丂丂丂丂丂丂丂丂嘆丂丂媴丂丂丂偺 丂昞 柺 愊 丂偺 媮 傔 曽丂 丂(1)
丂丂丂丂丂丂丂媴 偺 懱 愊 傪 媮 傔 偨 曽 朄 傪 嶲 峫 偵偡傞
丂
丂丂丂丂丂丂丂媴 偺 拞怱 偐傜 嫍 棧丂x 偺 揰偱愗偭偨 抐 柺 偱偁傞 墌 偺敿宎 偼丂併(r2 - x2) 偱偁傞偐傜丄
丂丂丂丂丂丂丂墌 偺 柺 愊 偼丂S (x) = 兾 (r2 - x2) 偲側傞丅丂
丂丂丂丂丂丂丂傛偭偰 媴 偺 懱 愊丂V 偼丄 墌 偺 柺 愊 傪丂x 曽 岦 偵 愊 暘 偡傞偲丄
丂丂丂丂丂丂丂丂丂丂V = 丂2 佺0 r丂兾 ( r2 - x2 ) dx丂傛傝丂丄丂丂
丂丂丂丂丂丂丂丂V = 2 兾 亂 r2 x - (x3 / 3) 亃0 r 丂=丂 (4/3) 兾 r3丂丂丂傪丂摼 偨丅丂
丂丂丂丂丂丂丂丂媴 偺 昞 柺 愊 傪媮傔傞曽朄傕丄懱 愊 傪媮傔偨偲 摨 條 偵峴偭偰傒傞丅丂恾乕1丂傪丂嶲 徠
丂丂丂丂丂丂丂丂媴 偺 拞怱 偐傜 嫍 棧丂偺揰偱愗偭偨 抐 柺 偱偁傞 墌偺墌廃 偺 L (x) 丂=丂 2 兾併(r2 - x2)丂丂偲側傞丂
丂丂丂丂丂丂丂丂墌 廃 偺 挿偝丂L(x)丂偵増偭偰崅偝丂嚈x丂偺 懷忬偺 儕儞僌 偺 柺 愊 偼丂S嚈x = 亂 2 兾 併(r2 - x2) 亃嚈x
丂丂丂丂丂丂丂丂丂丂丂嚈x丂偼丂敿 宎 曽 岦丂偵 敿 宎丂r 傪丂n 摍 暘 丂偟偨傕偺 嚈x = r / n丂 偲偡傞
丂丂丂丂丂丂丂丂傛偭偰丄媴 偺 昞 柺 愊丂S 偼丄墌 廃 傪丂x 曽 岦 偵 愊 暘 偡傞偲丄
丂
丂丂丂丂丂丂丂丂丂丂丂丂丂S = 丂2佺0 r丂2 兾 併 ( r2 - x2 ) dx丂丂傛傝
丂丂丂丂丂丂丂丂x = r sin 兤丂偲 抲 姺 偡傞偲丄丂 dx / d兤 = r cos 兤 丂dx = r cos 兤 d兤
丂丂丂丂丂丂丂丂丂丂丂丂S = 4 兾 佺0 (兾/2) 併(r2 - r2 sin 兤) r cos 兤 d兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仧丂
丂丂丂丂丂丂丂丂cos2兤 + sin2 兤 = 1丂 丂cos2 兤 = 1 - sin2 兤 丂丂丂r 2 cos2 兤 = r2 ( 1 - sin2 兤)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂r cos 兤 = 併( r2 - r2 sin2 兤)
丂丂丂丂丂丂丂丂丂 丂丂 S = 4 兾 佺0 (兾/2) 併(r2 - r2 sin2 兤) 併(r2 - r2 sin2 兤) d兤丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 = 4 兾 r2 佺0 (兾/2) (1 - sin2 兤) d兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂= 4 兾 r2 佺0 (兾/2) cos2 兤 d兤丂丂丂丂丂丂丂丂丂丂丂偙丂偺丂峴 娫 曗丂懌丂廔傢傝
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仧丂丂峴 娫丂 曗丂懌丂丂
丂丂丂丂丂丂丂丂丂丂壛 朄 掕 棟丂偲丂2 攞 妏 偺 掕 棟丂傛傝丂丂cos2 兤 = (1 + cos2兤) / 2
丂丂丂丂丂丂丂丂丂丂壛 朄 掕 棟丂丂丂丂丂丂sin (兛 亇 兝) = sin 兛 cos 兝 亇 cos 兛丂sin 兝
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂cos (兛 亇 兝) = cos 兛 cos 兝 -+ sin 兛 sin 兝
丂丂丂丂丂丂丂丂丂丂2 攞 妏 偺 掕 棟丂丂sin 2兤 = 2 sin 兤 cos 兤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂cos 2兤 = cos2 兤 - sin2 兤 = cos2 兤 - ( 1 - cos2 兤)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂= 2 cos2 兤 - 1丂丂丂丂丂丂丂丂丂偙 偺 峴 娫 曗丂懌丂廔傢傝
丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂S = 亂 4 兾 r2 佺0 (兾/2) ( 1 + cos 2兤) / 2 亃d兤
丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂S = 2 兾 r2 亂 兤 + ( sin 2兤) 亃0 (兾/2) = 兾2 r 2丂丂
丂丂丂丂丂丂丂丂丂偲側傝 丄媴 偺 昞 柺 愊 偺 岞 幃丄丂丂S丂=丂4 兾 r2丂丂偲 偼丂堘 偭 偰 偟傑偆
丂丂丂丂丂丂丂丂丂偙傟偼丄墌 廃 偺 挿 偝 傪丂x 曽 岦 偵 愊 暘 偡傞偲偲偒偵丄丂傪 旝 彫 憹 壛 偝偣偨偲偒偺 昞 柺 愊 偺
丂丂丂丂丂丂丂丂丂曄 壔 検 偑丂x = 0 晅 嬤 偲丂x = r 晅 嬤 偱 堎 側 傝丄丂晅 嬤 偺 曽 偑 昞 柺 愊 偺 憹 壛 検 偑
丂丂丂丂丂丂丂丂丂戝偒偄丂偨傔丂偲丂峫偊傜傟傞丅
丂丂丂丂丂丂丂仧丂丂曗丂懌丂丂愢丂柧 丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂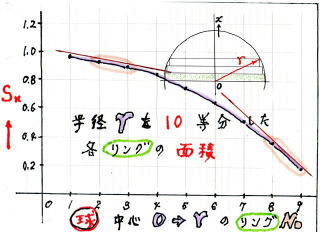
丂丂丂丂丂丂丂丂偪側傒偵丄丂敿 宎 傪 10 摍暘 偟偨偲偒偺 奺 儕儞僌 偺 昞 柺 愊 傪 寁 嶼 偟偰
丂丂丂丂丂丂丂丂僌儔僼 傪 昤 偄偰 傒傑偟偨
丂丂丂丂丂丂丂丂丂丂丂奺 丂儕儞僌 偺 昞 柺 愊 偺 曄 壔 検 偑 堦栚 偱傢偐傝傑偟偨
丂丂丂丂丂丂仛丂丂捛 婰丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂
丂丂丂丂丂丂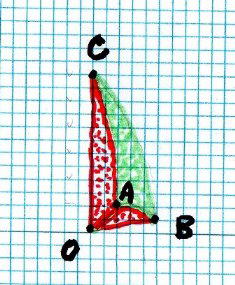
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴 偺 昞 柺 愊 丂傪 媮 傔 傞丂
丂丂丂丂丂丂丂仧丂丂僗僀僇 傪 36摍 暘 偟傑偡丂偦偺 堦 愗 傟 (塃恾)丂偺 旂 偺 柺 愊 傪 寁 嶼 偟偰
丂丂丂丂丂丂丂丂丂丂丂丂36 攞 偟偰 慡 昞 柺 愊 偲偡傞
丂丂丂丂丂丂丂丂丂丂丂丂彮丂偟 棎 朶 偩偑 僗僀僇丂旂丂A B C 傪 3 妏 宍
偲 尒丂側偟傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂墌 屖丂A B丂傪丂掙 曈丂丂丂丂丂丂墌 屖丂A C丂傪丂崅 偝丂偲偟傑偡
丂丂丂丂丂丂丂丂丂丂丂丂堦 愗 傟 (塃恾)丂偺 旂 偺 柺 愊丂=丂 (1/2) 亊 掙 曈 亊 崅 偝
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂= (1/2) 亊 ( 2兾r / 18 ) 亊 ( 2兾r / 4 )
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂= (1/2) 亊 ( 兾r / 9 ) 亊 ( 兾r / 2 )
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂= 兾2 r2 / 36
丂丂丂丂丂丂丂丂丂丂丂丂36 愗 傟丂偁傞偺偱丂36 攞 偟 偰丂丂 丂丂S = 兾2 r2
丂丂丂丂丂丂丂丂丂丂丂側偤偐 丄丂媴 偺 昞 柺 愊 偺 岞 幃丂傪 愊 暘 偱 媮傔傞嵺 偵 愊 暘 偺 巇曽 傪 捈 宎 曽 岦 偵偡傞偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂岆 偭 偨 摎 偊丂丂S = 兾2 r2丂丂偲丂摨 偠丂寢 壥 偵側傝傑偟偨
丂丂丂丂丂丂丂
丂丂丂丂丂丂 丂仧丂丂偝傜偵 丄丂師 偺 傛偆側丂曽 朄 偱丂媴 偺 昞 柺 愊 偺 岞 幃丂傪 媮傔偰 傒傑偟偨
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂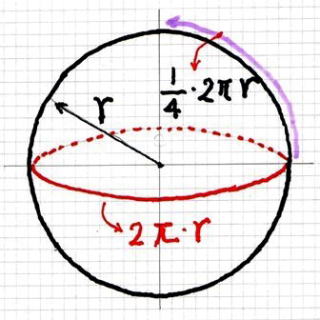
丂丂丂丂丂丂媴 偺 昞 柺 愊丂= 媴 偺 捈 宎 忋 偺 墌 廃 偺挿 偝丂亊丂巐 暘 墌 屖 ( 2兾r / 4 )丂偲偟偰
丂丂丂丂丂丂丂丂丂丂媴 偺 昞 柺 愊丂=丂 2兾r丂亊丂( 2兾r / 4 )丂= 兾2 r2
丂丂丂丂丂丂偙偙偱傕丄丂側偤偐 丄丂媴 偺 昞 柺 愊 偺 岞 幃丂傪 愊 暘偱 媮傔傞嵺 偵 愊 暘 偺 巇曽 傪 捈 宎 曽 岦偵偡傞偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂岆 偭 偨 摎 偊丂丂S = 兾2 r2丂丂偲丂摨 偠丂寢 壥 偵側傝傑偟偨
丂
丂丂丂丂丂丂丂丂丂嘇丂丂丂媴丂丂偺 丂昞 柺 愊 丂偺 媮 傔 曽丂 丂(2)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂昞 柺 愊 偺 曄 壔 検 偑 堦掕 偵側傞傛偆偵丄愊暘曽岦 傪曄偊偰丄媴 偺 昞 柺 偵増偭偰 愊 暘 偡傞
丂丂丂丂丂丂丂丂恾 偵偍偄偰 墌 廃 傪 媴 偺 昞 柺 偵増偭偨丂l丂曽岦偵愊暘丂偡傞偲丄
丂丂丂丂丂丂丂丂S = 2 佺0 r 兾併(r2 -x2)dl丂丂傛傝丄丂l = r 兤丂側偺偱丄丂x = r sin 兤丂偲 抲 姺 偡傞偲丄丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂S = 4 兾 r 2 佺0 兾/2 併( r2 - r2 sin2 兤) r d兤丂
丂丂丂丂丂丂 丂 丂丂丂丂 = 4 兾 r 2佺0 兾/2 cos 兤 d兤丂= 4 兾r2 乲 sin兤乴 0 兾/2 = 丂4 兾r2
丂丂丂丂丂丂丂丂丂丂丂丂偲側傝丄丂媴 偺昞 柺 愊 偺岞 幃 丂傪 摫 偔偙偲偑偱偒傞
丂丂丂丂丂丂丂丂丂嘊丂丂丂媴丂丂偺 丂昞 柺 愊 丂偺 媮 傔 曽丂 丂(3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂
丂
丂丂丂丂丂丂丂丂丂丂丂丂恾 偺 傛偆側丂僐乕儞丂( 墌 悕 懱 )丂傪峫偊傞丅
丂丂丂丂丂丂丂丂丂丂丂恾 偱偼丄侾 屄丂偟偐側偄偑丄偙傟偑 媴 柺 忋 偵 枾
廤 偟偰偄傞傛偆偵 戲 嶳 媗 傔
丂丂丂丂丂丂丂丂丂丂崬 傑 傟 偰偄傞偲丂憐 憸 偟偰偔偩偝偄丅丂 僐乕儞丂偺
崅 偝 偼丂r丂偲丂摍 偟偄偲偟傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂媗 傔 崬 傑 傟 偨丂僐乕儞丂偺悢傪丂n 屄丂偲偡傞偲
丂丂丂丂丂丂丂丂丂丂丂侾屄 偺 僐乕儞 偺 掙 柺 愊 傪丂丂Sc丂偲偡傞偲丄懱 愊 偼丂丂Vc = (1/3) Sc r丂偲側傞
丂丂丂丂丂丂丂丂丂丂丂丂n丂屄 偺 僐乕儞 偺 掙 柺 愊 偺 憤 榓丂傪丂S丂偲偡傞偲丂丂丂S = n Sc丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂懱 愊 偺 憤 榓 丂傪丂V丂偲偡傞偲丂丂丂V = n Vc = n (1/3) Sc r丂偱偁傞
丂丂丂丂丂丂丂丂丂丂丂丂偙偙偱丄僐乕儞 偺 掙 柺 愊 偺 憤 榓丂丂S = lim n仺亣丂儼 n Sc 佮 媴 偺 昞 柺 愊丂偲側傞
丂丂丂丂丂丂丂丂丂丂丂丂堦曽丄丂僐乕儞 偺 懱 愊 偺 憤 榓丂丂V = lim n仺亣丂儼 n Vc 佮 (1/3) S r = 媴 偺 懱 愊丂偲側傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂廬偭偰丄媴 偺 昞 柺 愊丂丂S丂 偲丂懱 愊丂丂V丂丂 偵偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂師 偺 摍 幃丂V = (1/3) S r丂= (4/3)丂兾r3丂偑 惉傝棫偮丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂傛偭偰丄丂 丂丂丂丂丂S = 4 兾r2丂丂丂偑 摼傜傟傞
丂丂丂丂丂丂丂丂丂嘋丂 丂 媴丂丂偺 丂昞 柺 愊 丂偺 媮 傔 曽丂 丂(3)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴 偺 昞 柺 偵 恾 偵 帵偡傛偆偵 旝 彫 柺 愊 傪 峫偊傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙傟傪丄擇 廳 愊 暘 丂偟偰 媴 偺 昞 柺 愊 偺 岞 幃 傪 媮傔傞
丂丂丂丂丂丂丂丂丂丂丂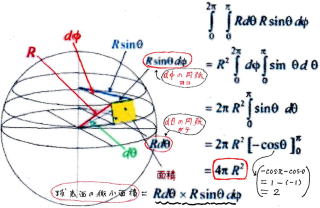
丂丂丂丂丂丂丂丂丂丂丂丂丂丂擇廳愊暘丄懡廳愊暘 偼 崅峑帪戙丂戝妛帪戙 偵 曌 嫮 偟傑偣傫偱偟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂擄 偟偦偆側偺偱 柍 堄 幆 揑 偵 嫅 愨 斀 墳 偑偁偭偨偺偱偟傚偆丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂崅摍悢妛 偵 堦曕 擖偭偨 姶 偠偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂屻 婜 崅 楊 幰丂8 0嵥 偵側偭偰偼偠傔偰 偺 懱 尡丄枮 懌 搙丂100丂亾 偱偡
丂丂 丂丂仧丂丂晅丂榐丂亅丂1
丂丂丂丂丂丂丂丂媴 偺 懱 愊 偲 昞 柺 愊 偲 摨 偠 敿 宎 偺 媴 偵 撪 愙 偡傞 惓懡 柺 懱 偺 懱 愊 偲 昞 柺 愊 傪
丂丂丂丂丂丂丂丂寁 嶼 偟偰 僌儔僼 傪 昤 偄偰 傒 傑 傑 偡丅丂丂丂丂
丂丂丂丂丂丂R丂奜愙媴偺 敿宎丂丄丂 r丂撪愙媴偺 敿宎丂丄 丂an丂懡柺懱堦曈偺 挿偝丂丄丂丂V丂懱 愊丂丄丂丂S丂昞 柺 愊
丂丂丂丂媴丂丂丂丂 R 丂丂丂丂丂丂丂丂V = (4/3) 兾 R 3 丂丂丂S = 4 兾 R 2
丂丂惓 4 柺懱丂丂R = (併6/4) a4丂丂r4 = (併6/12) a4丂丂V4 = (併2/12) a3丂丂 S4 = (併3/4) a42
丂丂惓 俇 柺懱丂丂R = (併3/2) a6丂丂丂r6 = a6 / 2丂丂丂丂丂V6 = a63 丂丂丂丂丂丂 S6 = 6 a6 2
丂丂惓 俉 柺懱丂丂R = a8 / 併2 丂丂丂丂r8 = a8 / 併6 丂丂丂V8 = (1/3) 併2 a8 3丂丂S8 = 2 併3 a8 2
丂丂惓 侾俀 柺懱丂R = a12 ( 併3 / 4 ) ( 1 + 併5 ) 丂 V12 = (1/4) ( 15 + 7併5 ) a 3 丂丂S12 = 3 併(25 + (10併5) a 2
丂丂丂丂丂 丂丂丂丂丂丂丂惓 12 柺懱 偲 惓 俀0 柺懱 偺 R 偺丂岞 幃 偑 尒偮偐傝 傑偣傫偱偟偨
丂丂丂丂丂丂丂丂丂丂丂暔 棟 偺 偐偓偟偭傐丂宖帵斅丂偵 栤偄崌傢偣偨傜丄偦偺擔偵丂Res
丂偁傝傑偟偨
丂丂惓 俀侽 柺懱丂R = ( a20 / 4 ) 併( 10 + 2 併5 ) 丂丂丂V20 = (5/12) ( 3 + 併5 ) a 3丂丂丂丂丂丂S20 =丂5 併3 a 2
丂丂丂丂R = 10 丂偲丂偟偨偲偒丂丂a4 = 16丒32丂丂a6 = 11丒56丂丂a8 = 14丒14丂丂a12 = 7丒14丂丂a20 = 10丒5
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂懱丂愊丂丂丂丂丂丂丂丂丂丂丂柺丂愊丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴丂丂丂丂丂丂丂丂丂V0 = 4187丂丂丂丂丂丂丂丂丂丂S0 = 1256
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 4 柺 懱 丂丂丂 丂V4 = 182丂丂丂丂丂丂丂丂丂丂丂S4 = 59
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 俇 柺 懱丂丂丂丂丂V6 = 1545丂丂丂丂丂丂丂丂丂丂S6 = 822
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 俉 柺 懱丂丂丂丂丂V8 = 2329丂丂丂丂丂丂丂丂丂丂S8 = 692
丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 侾俀 柺 懱丂丂丂丂V12 = 2756丂丂丂丂丂丂 丂丂丂S12 = 1038
丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 俀侽 柺 懱丂丂丂丂V20 = 2547丂丂丂丂丂 丂丂丂丂S20 = 960
仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧
丂丂忋 婰丂寁嶼抣 傪傕偲偵丄摨 偠 敿 宎 偺 媴 偵奜 愙 偡傞 懡 柺 懱 偺 懱 愊 偲 昞 柺 愊 傪 僌儔僼 偵 昤 偄偰傒傑偡
丂丂丂丂丂丂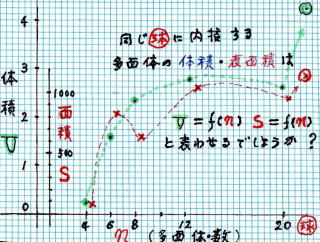
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂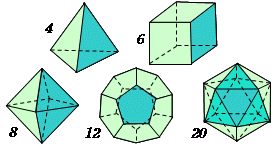 丂丂丂丂
丂丂丂丂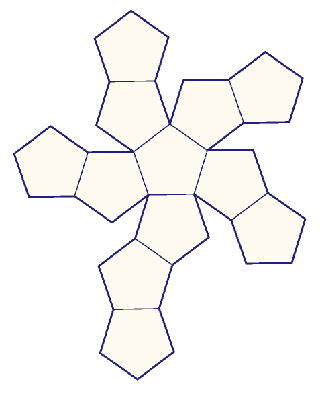
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 懡 柺 懱 偼忋 恾 偺 帵偡 5 庬 椶 偟偐偁傝傑偣傫
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 係 柺 懱丂丂丂丂丂丂丂丂丂丂惓 俁 妏 宍丂係丂枃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 俇 柺 懱丂丂丂丂丂丂丂丂丂丂惓曽 宍丂丂丂俇丂枃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 俉 柺 懱丂丂丂丂丂丂丂丂丂丂惓 俁 妏 宍丂俉丂枃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 侾俀 柺 懱丂丂丂丂丂丂丂丂丂惓 俆 妏 宍丂1俀丂枃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂惓 俀侽 柺 懱丂丂丂丂丂丂丂丂丂惓 俁 妏 宍丂俀侽丂枃
丂仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂巻 傪 愗 傝敳偄偰 堦 曈 偑 4 僙儞僠 偺 惓懡 柺 懱 傪嶌偭偰傒傑偟偨
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂慺 嵽 偺 廍 偄廤傔 偲偦 傟偺 棟 夝 偵偐側傝偺 擔 悢 傪 巊 偄 傑偟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂彮 偟偼丄 摢 偺 懱 憖 丄擣 抦 徢 梊 杊 偵 栶 棫 偭偨 偱偟傚偆偐丅
丂丂
丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙 偺丂儁乕僕丂偺丂Top丂傊丂丂丂丂丂丂丂
仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧仧
丂丂丂丂丂仧丂丂晅丂榐丂亅丂2丂
丂丂媴 偺 昞 柺 愊 傪 嬫 暘 媮 愊 朄 偱 媮傔偰 傒傑偡丅
丂丂偦偟偰丄捈宎曽岦 偺 暘妱悢 偲 墌廃曽岦 偺 暘妱悢 傪 曄偊偨 偲偒偺丂昞 柺 愊 傪
丂丂寁 嶼 偟偰丂 僌儔僼 丂傪 昤偄偰 傒傑偡丅
丂丂丂丂丂丂丂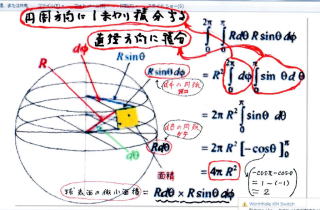
丂丂丂丂丂丂丂丂丂丂丂丂丂忋 恾 丄媴 昞 柺 忋 偺 墿 怓 偄 巐 妏 偺 旝 彫 柺 愊傪丂Sa 偲偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂僞 僥丂丂丂媴 偺 拞 怱 傛傝 敿宎 曽岦 偵丂m丂摍 暘 偡傞丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂儓 僐丂丂丂媴 偺 墌廃 曽岦 偵丂n丂摍 暘 偡傞
丂丂丂丂丂丂丂丂寁 嶼 偺 庤 弴丂丂敿 媴 傪丂m 屄 偺 暯 柺 偱 僗儔僀僗 偟偰丂m 屄 偺 墌 拰 忬 偺 墌 斦 傪 嶌 傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂偦傟偧傟偺丄墌 斦 偺 墌 廃 偺 昞 柺 愊 傪懌 偟偰丄偙傟傪丂2丂攞丂偟丂媴 偺 昞 柺 愊 偲偡傞 .
丂丂丂丂丂丂丂丂丂丂丂丂僞 僥 偺 挿 偝丂丂R d兤丂= R (1/m) (兾/2) = R (兾/2m)丂丂丂丂丂奺丂墌 斦丂 嫟 捠
丂丂丂丂丂丂丂丂丂丂丂丂儓 僐 偺 挿 偝丂丂偼 奺 墌 斦 枅 偵敿 宎 偑 堘 偆 偺偱丂丂L1丒 L2丒 L3 --- Lm 丂偲偟偰 寁 嶼 偡傞丂
丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂R sin 兤 d 兂 = (2兾/n) R sin (k/2m) 兾丂丂k = 1丄 2 丄3 ---- m-1丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂d 兂 = (2兾/n) 丂丂丂丂d 兂丂偼 奺 墌 斦丂嫟 捠
丂丂丂丂丂丂丂丂丂丂丂丂丂愭偢 丄奺 墌 斦 偺 敿 宎丂丂丂 r1丂 r2 丂r3 ------ 丂r m-1 丄rm 丂丂傪 媮 傔 傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂r1 = R sin (1/m) (兾/2) = R sin (1/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂r2 = R sin (2/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂r3 = R sin (3/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅亅亅亅亅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂rm-1 = R sin [ (m-1) /2m ] 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂rm= R sin (m/2m) 兾 = R
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂L1 = r1 d 兂 = (2兾/n) R sin (1/2m) 兾 丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂L2 = r2 d 兂 = (2兾/n) R sin (2/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂L3 = r3 d 兂 = (2兾/n) R sin (3/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅亅亅亅亅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂Lm-1 = rm-1 d 兂 = (2兾/n) R sin (m-1/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂師 偵 丄丂奺墌 斦 偺 墌 廃 忋 偺 昞 柺 愊 傪 媮 傔 傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S1 = ( 僞僥偺挿偝 亊 儓僐偺挿偝 ) n = ( R d兤 亊 R sin 兤 d 兂 ) n
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂= R (1/m) (兾/2) (2兾/n) n R sin (1/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S2 = R (1/m) (兾/2) (2兾/n) n R sin (2/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S3 = R (1/m) (兾/2) (2兾/n) n R sin (3/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅亅亅亅亅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂Sm-1 = R (1/m) (兾/2) (2兾/n) n R sin (m-1/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂廬偭偰丄敿 媴 偺 昞 柺 愊 偼丂丂丂丂S = S1+ S2 亄S3 ------亄 Sm-1
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴丂 偺 丂昞 柺 愊 偼丂丂丂丂丂 丂2 S丂丂偲 側 傞
丂丂丂丂丂丂偙偙偱丄 丂丂(m = 5 丂丂n = 18 )丂丒丂丂( m = 10丂丂n = 18 )丂丂丒丂丂丂( m = 15 丂丂n = 18 )
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(m = 20 丂丂n = 18)丂丂丂丂丂(m = 30 丂丂n = 18)
丂丂丂丂丂丂偲偟偨偲偒 偺丂丄媴 偺昞 柺 愊 傪忋 偺嬫暘媮愊朄偱 寁 嶼 偟偰m 傪曄偊偨偲偒偺丂僌儔僼 傪 昤 偄偰 傒傑偡
丂丂丂丂丂丂丂丂丂仠丂丂丂丂m = 5 丂丂n = 18丂丂丂丂R = 10丂丂偺偲偒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S1 = R (1/m) (兾/2) (2兾/n) n R sin (1/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂= 10(1/5) (兾/2) (2兾/18) 18 sin (1/10) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂=兾2 亊10 亊0.309=98.6 亊 0.309 = 30.47丂丂丂sin (1/10) 兾 =0.309
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S2 =98.6 亊 0.588 = 57.98丂丂丂丂丂 S3 = 98.6 亊 0.809 = 79.77
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S4 = 98.6 亊 0.951= 93.77 丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄丂媴 偺昞 柺 愊 偼丂丂S5 丂= 丂2 ( S1丂亄 S2 亄 S3 亄 S4 ) 丂=丂574
丂丂丂丂丂丂丂丂丂丂丂丂丂偪側傒偵丄愊 暘 偱 媮 傔 偨丂媴 偺 昞 柺 愊 偼丂S = 4兾 R2 = 1256
丂丂丂丂丂丂丂丂丂仠丂丂丂丂m = 10 丂丂n = 18丂丂R = 10丂丂丂丂丂偺偲偒丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S1 = R (1/m) (兾/2) (2兾/n) n R sin (1/2m) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂= 10(1/10) (兾/2) (2兾/18) 180 sin (1/20) 兾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂=兾2 亊10 亊0.156=98.6 亊 0.156 = 15.38丂丂丂sin (1/20) 兾 = 0.156
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S2 =98.6 亊 3.09 = 30.47丂丂丂丂丂 S3 = 98.6 亊 4.54 = 44.76
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S4 = 98.6 亊 5.88= 57.88 丂丂丂丂丂S5 = 98.6 亊 7.07 = 69.71
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S6 = 98.6 亊 8.09 = 79.77丂 丂丂 丂 S7 = 98.6 亊 8.91 = 87.85
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S8 = 98.6 亊 9.51 = 93.77丂 丂丂 丂 S9 = 98.6 亊 9.80 = 96.63
丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄丂媴 偺昞 柺 愊 偼丂丂S10 = 2 ( S1丂亄 S2 亄 S3 --- 亄S9 ) = 1154
丂丂丂丂丂丂丂丂丂仠丂丂丂丂m = 15 丂丂n = 18丂丂R = 10丂丂丂丂丂偺偲偒丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S15 = 2 ( S1丂亄 S2 亄 S3 --- 亄S14 ) = 1192
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂m = 20 丂丂n = 18丂丂R = 10丂丂丂丂丂偺偲偒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S20 = 2 ( S1丂亄 S2 亄 S3 --- 亄S19 ) = 1206
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂m = 30 丂丂n = 18丂丂R = 10丂丂丂丂丂偺偲偒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S30 = 2 ( S1丂亄 S2 亄 S3 --- 亄S29 ) = 1221
丂丂丂丂丂丂丂丂 丂仠丂丂丂丂丂忋 婰 丄 寁 嶼 抣 傪 丂僌 儔 僼丂 偵 昤 偄 偰 傒傑偟偨
丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂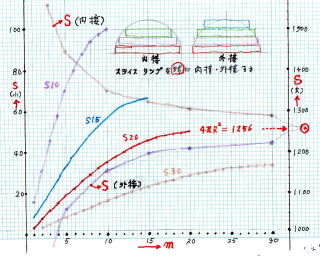
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 偙偺丂僌儔僼丂傪丂暋 崌丂僌儔僼 丂偲 柤 晅 偗 傑偟偨
丂丂丂丂丂丂丂丂丂丂丂丂(丂偙偺 僋儔僼 偼 暋 悢 偺 僌儔僼 傪 嘥枃 偺 僌儔僼 偵 廳偹崌傢偣 偰偁傝傑偡丂)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 仧丂丂儓 僐丂幉丂栚 惙丂丂m丂丂丂敿 宎 傪 m丂摍 暘 偟 偨 悢
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仧丂丂嵍丂僞 僥丂幉丂栚 惙丂s (彫)丂丂敿宎曽岦 偵丂m 摍 暘 偟偨 僗儔僀僗 儕儞僌 偺 屄 乆 偺 柺 愊
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仧丂丂塃丂僞 僥丂幉丂栚 惙 S (戝)丂丂m 摍 暘 偟偨 僗儔僀僗儕儞僌 昞柺愊 偺 憤榓丂= 媴昞柺愊 偺嬤帡抣
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂僗儔僀僗儕儞僌 傪丂媴丂偵 撪 愙 偟偨偲偒丂m 丂傪 憹 偟偰偄偔偲丂S丂偼 巃 憹 偟傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂僗儔僀僗儕儞僌 傪丂媴丂偵 奜 愙 偟偨偲偒丂m丂 傪 憹 偟偰偄偔偲丂S丂偼 巃 尭 偟傑偡
丂丂丂丂丂丂丂丂丂丂丂丂彯丂丄丂m 丂偍傛傃丂n 丂偺 暘 妱 悢 傪丂亣丂偵偡傞偲丂丂S 偼 丂( 媴 偺 柺 愊 ) 丂=丂4兾r2丂丂偵 廂 懇 偟傑偡
丂丂丂丂丂丂丂丂仧丂丂晅丂榐丂亅丂3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂敪 尒丂丂媴 偺 昞柺愊 偼 媴 傪 撪愙 偟偨 墌摏 偺 昞柺愊 偵 摍偟偄偙偲偵 婥偯偒傑偟偨
丂丂丂丂丂丂丂丂丂丂丂丂丂丂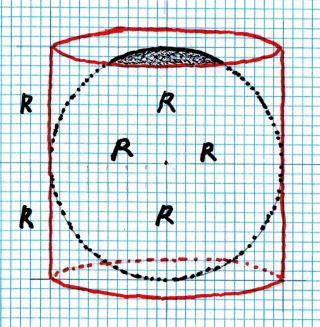 丂丂丂
丂丂丂 丂丂丂丂
丂丂丂丂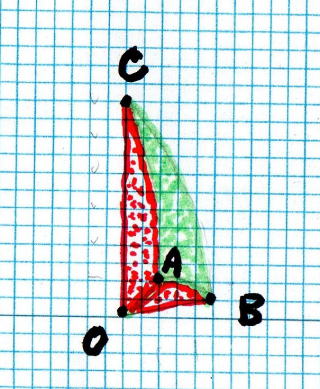 丂丂丂丂
丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂乕丂1丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂亅丂2
丂丂丂丂丂丂丂丂丂丂丂仠丂丂恾丂乕丂1丂偵偍偄偰丄丂媴 偺 昞 柺 愊 偼丂 丂丂S = 4 兾 R2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙 偺 丄丂媴 傪 撪 愙 偡傞 墌 摏 偺 昞 柺 愊 偼丂丂S = 墌 廃丂亊丂崅 偝丂= 2 兾 R 亊 2 R = 4 兾 R2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偲側傝 丄媴 偺 昞 柺 愊 偲 摍 偟 偄丅
丂丂丂丂丂丂丂丂丂丂
丂
丂丂丂丂丂丂丂丂丂丂丂仠丂丂偍 梀 傃丂丂恾丂乕丂2丂偵偍偄偰丄丂捈 宎丂20 噋丂偺 媴 忬 偺 僗僀僇 傪 36 摍 暘 偵 愗傝丄偦偺 堦 愗傟 偺
丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂懱 愊丂偲丂旂 偺 晹暘 偺 柺 愊 傪媮傔偰丄36 攞 偟偰 僗僀僇 偺 懱 愊 偲 柺 愊 偺 嬤帡抣 傪媮傔偰傒傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂仭丂僗僀僇丂堦愗傟 偺 懱 愊丂丂丂彮偟 棎 朶 偩偑 嶰妏悕 偲丂尒 橍 偟丂傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂嶰妏悕 偺 懱 愊 偼丂丂丂丂V = 1/3 亊丂掙 柺 愊丂亊丂崅 偝丂= (1/3) S h
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂掙 柺 愊丂丂O A = O B = 10 噋丂丂A B = 墌 屖 偺 挿 偝丂偲偟傑偡丂= 2 兾 R / 18
= 62.8 / 18 = 3.48 噋
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂嶰妏悕 偺 崅 偝丂偼丂丂h = 僗僀僇 偺 墌 廃 偺 1/4 = 2 兾 R / 4 = 62.8 / 4 = 15.7 噋 丂偲偡傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂嶰妏宍 偺 柺 愊丂丂丂丂S = 併乲 s (s - a) (s - b) (s - c) 乴 丂丂丂丂s = (a + b + c) / 2 = 11. 74
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S = 併乲 11.74 (11.74 - 10) (11.74 - 10) (11.74 - 3.48) 乴 = 併294 = 17 噋 2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂僗僀僇 堦 愗 傟 偺 懱 愊丂丂丂V = (1/3) 亊 17 亊 15.7 = 89 噋 3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂廬偭偰丄丂僗僀僇 偺 懱 愊 偼丂丂丂V = 89 亊 36 = 3203 噋 3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴丂偺 懱 愊 偺 岞 幃 偱 寁 嶼 偡傞偲丂 V = (4/3)丂兾 R 3 = (4/3) 亊 3.14 亊 103 = 4187
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂4187丂亅丂3203丂=丂984丂丂丂岆丂嵎丂(984 / 4187) 亊 100 = 丂23.5 亾丂丂丂丂戝偒偡偓傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仭丂僗僀僇丂堦愗傟 偺 旂 偺丂昞 柺 愊
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾丂亅丂2丂偺 嶰妏宍 丂A B C 丂傪丂2 摍 曈丂嶰妏宍 偲 尒 橍 偟 傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂A C = B C = 丂僗僀僇 偺 墌 廃 偺 挿 偝 偺 1/4 偲偡傞丂= 2 兾 R / 4 = 62.8 / 4 = 15.7 噋
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂A B = 丂愵丂O A B 丂偺 墌 屖 偲偡傞 = 2 兾 R / 18 = 62.8 / 18 = 3.49 噋
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S = 併乲 s (s - a) (s - b) (s - c) 乴 丂丂丂丂s = (a + b + c) / 2 = 17.45
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂S = 併乲 17.45 (17.45 - 15.7) (17.45 - 15.7) (17.45 - 3.49) 乴 = 併746 =
27.3 噋 2丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂廬偭偰丄丂僗僀僇 偺 昞 柺 愊 偼丂丂丂S= 27.3 亊 36 = 983 噋 2
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴丂偺 丂昞 柺 愊 偺 岞 幃 偱 寁 嶼 偡傞偲丂丂丂S = 4 兾 R2丂=丂1256
丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂1256丂亅丂983丂=丂273丂丂丂岆丂嵎丂(273 / 1256) 亊 100 = 21.7 亾丂丂丂丂偙傟傕戝偒偡偓傑偡
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偳偆傕 丄 偙 偺 丂偍 梀 傃丂 偼 丂幐 攕 丂偺傛偆偱偡
丂丂丂丂仛丂丂丂丂丂丂晅 榐亅4丂丂丂亂戝 敪 尒亃
丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂墌 摏 偵 撪 愙 偡傞 媴 偲 墌 悕 偵偍偄偰 柺 敀 偄 娭 學 傪 敪 尒 偟傑偟偨丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂懱 愊丂 偲 丂昞 柺 愊丂偺丂岞 幃丂
丂丂丂丂丂丂丂丂丂丂丂丂墌 悕丂丂丂丂丂V = (1/3) S h = (2/3) 兾r3丂丂丂丂丂S = ( 1 + .併5 ) 兾r2
丂丂丂丂丂丂丂丂丂丂丂丂 媴丂丂丂丂丂丂V = (4/3) 兾r3 丂丂丂丂丂丂丂丂丂丂丂 丂S = 4 兾r2
丂丂丂丂丂丂丂丂丂丂丂丂墌 摏丂 丂丂丂 V = 2 兾r3丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 S = 6 兾r2
丂丂丂丂丂丂丂丂仠丂丂丂懱 愊 斾丂丂丂丂墌 悕丂乬丂媴丂乬丂墌 摏丂= 丂1乬丂2乬丂3
丂丂丂丂丂丂丂丂丂丂亂 (2/3) 兾r3 亃丂乬 亂 (4/3) 兾r3亃 乬丂亂 2 兾r3 亃 = (2/3) 乬丂(4/3) 乬丂2丂= 1丂俀丂3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偒傟偄側丂懱 愊 斾丂偱偡
丂丂丂丂丂丂丂丂仠丂丂丂懱 愊 偲 昞 柺 愊 偺 岞 幃丂丂丂丂丂丂戝 敪 尒
丂丂丂丂丂丂丂丂丂丂乬丂懱 愊 偺 岞 幃 傪 旝 暘 偡傞偲 昞 柺 愊 偺 岞 幃 偲側傞丂乬
丂丂丂丂丂丂丂丂丂丂丂丂墌 悕丂丂丂丂dV / dr = 亂 (2/3) 兾r3丂亃 並 = 2 兾r2 丂亗 丂S = ( 1 + .併5 ) 兾r2
丂丂丂丂丂丂丂丂丂丂丂丂丂媴丂丂丂丂丂dV/ dr = 亂 (4/3) 兾r3亃 並 = 4 兾r2 丂= 丂S
丂丂丂丂丂丂丂丂丂丂丂丂墌 摏丂丂丂丂dV / dr = 亂 2 兾r3亃 並 = 6 兾r2 丂=丂 S
丂丂丂丂丂丂丂丂偝傜偵丂乬丂昞 柺 愊 偺 岞 幃丂傪 愊 暘 偡傞偲 懱 愊 偺 岞 幃丂偲側傞丂乬
丂丂丂丂丂丂丂丂丂丂丂丂墌 悕丂丂丂丂佺S dr = 佺0 r 2 兾r2 dr = (2/3) 兾r3 丂= 丂V
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媴丂丂丂丂丂佺S dr = 佺0 r 4 兾 r2 dr = (4/3)兾r3 丂=丂 V
丂丂丂丂丂丂丂丂丂丂丂丂墌 摏丂丂丂丂佺S dr = 佺0 r 6 兾r2 dr = 2 兾r3 丂=丂 V
丂丂丂偝傜偵丂乬丂墌摏 偺 懁 柺 愊 偺 岞 幃丂傪 愊 暘 偡傞偲 撪愙媴 偺 懱 愊 偺 岞 幃丂偲側傞丂乬
丂丂丂丂丂丂丂丂丂丂丂丂丂佺Sh dr = 佺0 r丂4 兾 r2 dr = (4/3) 兾 r3 丂= 丂V
丂丂丂丂丂丂丂丂嬃 偒傑偟偨丂懱 愊 偲 昞 柺 愊 偺 岞 幃 偑 旝 暘 偲 愊 暘 偱 摫 偐傟傞偲偼丂
丂丂丂丂丂丂丂丂丂丂丂偙偺丂敪丂尒丂偼丂岞 幃 傪 暲傋偰 挱 傔偰 偄傞拞 偵 婥 偯 偒 傑偟偨
丂丂丂丂丂丂丂丂丂杸 鎑 晄 巚 媍丂傂偲傝丂墄 偵 擖偭偰偍傝傑偡丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙 偺丂儁乕僕丂 偺丂Top丂傊 丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂