
 np - 77
np - 77
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★


アインシュタイン 1922 年 東 北 大 来 校
アインシュタイン は 1905 年 に 特 殊 相 対 性 理 論 を 発 表 しました
特 殊 相 対 性 理 論 は 主 に 光 り に 関する 理 論 でした
その後 10 年 かけて これ を バージョン アップ して 一 般 相 対 性 理 論 を 発 表 しました 1916 年
アインシュタイン 方 程 式 は 一般 相対性理論 における 重 力 場 を 記 述 する 場 の 方 程 式 である
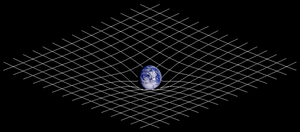
重 力 による 時 空 の ゆがみ

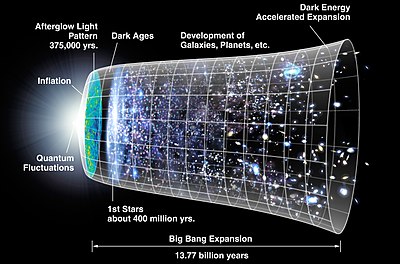
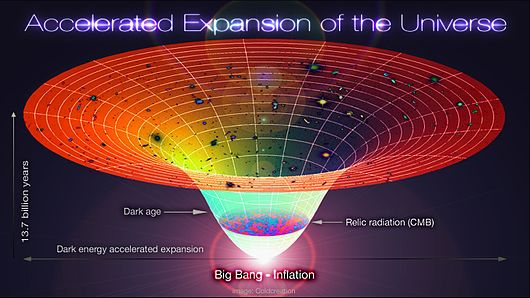
宇 宙 の 誕 生 Big Bang Big Bang Inflation
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
アインシュタイン 方 程 式 Yahoo よ り
参 考 資 料
アインシュタイン方程式 - Wikipedia 宇宙定数 - Wikipedia 万有引力定数 - Wikipedia テンソルの概念 [物理のかぎしっぽ]
計量テンソル [物理のかぎしっぽ] 時空の計量テンソル リッチテンソル - Wikipedia テンソルの一般的表現 [物理のかぎしっぽ]
エネルギー・運動量テンソル - Wikipedia アインシュタインテンソル - Wikipedia アインシュタイン方程式の導出
宇 宙 項 と は - コ ト バ ン ク ベクトル の 内 積 リーマン 多 様 体 - Wikipedia 少しわかつてきた 【 一般相対性理論 】
アインシュタイン 方 程 式 は ニュートン が 導いた 万有引力 の 法則 を、強い重力場 に対して 適用 できるように
拡 張 した 方 程 式 であり 中性子 星 や ブラックホール などの 高密度・大質量天体や、 宙全体 の 幾何学 などを 扱える
概略 や 導 出・ 応 用 などの 詳しい 説 明 については 「 一般相対性理論 」 を 参 照
法 則 の 辞 典 の 解 説
アインシュタイン 方程式 【 Einstein equation 】
一般 相対性 理論 においては, 時 空 を 四次元 の リーマン 空 間 と考えて, 物 体 の 運 動 は 空 間 によって 定まるものと考える.
逆に考えると,この 空 間 の 性質は,存在する物質 と 場 の 運 動 量,エネルギー の テンソル Tij に よって 定められる.
この関係 を 与える式 を アインシュタイン 方 程 式 という
Rμν ー (1/2) Rgμν 〓 ( 8πG / c 4 ) T μν 1905 年 初 期 の 重 力 方 程 式
Gμν + ∧ gμν 〓 k Tμν 1916 年 宇 宙 項 を 追 加
左 辺 は 時 空 が どのように 曲がって いるのか ( 時 空 の 曲 率 ) を 表す 幾 何 学 量 であり、
右 辺 は 物 質 場 の 分 布 を 表す 量 である
この 方 程 式 は 非 線 形 10 元 偏 微 分 連 立 方 程 式 という
追 記 【 10元 連立 2 階 偏微分 方程式 】 Yahoo 検 索 よ り 2019 8 4
アインシュタイン の 重 力 方 程 式 は 、10 個 の 関 数 に対する 2 階 の 偏微分 で 非線形 な 連立方程式 です。
その形は下の 画 像 をご覧ください。
この方程式は、宇 宙 の 構 造 を 決める とき 基本 となる 方 程 式 です。
「 重量場 の 方程式 」 とも 呼ばれ 、リーマン 幾何学 を 基 礎 にした 十元 連立 非線形 偏微分 方程式 です。
4次元時空 ( X、Y、Z、ct ) のうちの 2 つ の 組み合わせ の 数、すなわち 10 通 り のそれぞれについての、
「 時空 の 歪み 」 と 「 物質 のもつ エネルギー 」 の 満たすべき 関 係 を 含んでいます。
左辺 は 時空 の 曲がり 、すなわち 重 力 場 を 意 味 し 、右辺 は 物 質 エネルギー、
電 磁 場 や 宇 宙 にあるすべての 粒 子 の エネルギー の 全 体 を 意 味 します。
アインシュタイン は、宇宙 は 膨 張 も 収 縮 もしない 恒常的 な大きさ であると 考えていました。
宇 宙 が 収 縮 して 潰 れないように 重 力 と 反 対 の 斥 力 が 働いていると 考え、Λ ( ラムダ ) という 宇宙項 を 導入 しました。
しかし、ハップル によって 宇 宙 が 膨 張 している ことが 証 明 されると アインシュタイン は Λ の 導入 を
「 わ が 生 涯 最 大 の 過 ち 」 と 言った そうです。
ちなみに、私には 何のこっちゃか サッパリ わかりませんのでご 了承 ください。
【参考】
http://homepage2.nifty.com/m-traveller/tensor.htm

記 号 の 説 明
G ニュートン の 重 力 定 数 万 有 引 力 定 数 G = 6.67408(31)×10-11m3kg-1s-2
F1 = F2 = G ( m1 × m2 ) / r 2 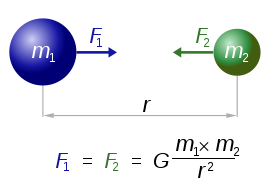 よ り
よ り
Rμν リツチ テンソル R は スカラー 曲 率
微分幾何学 において、リッチ曲率 テンソル ( 英: Ricci curvature tensor ) とは、
歪んだ リーマン 多様体上 の 測地球 の 体積 が ユークリッド 空間上 の 球体 からどれだけ ずれ るかを
表す 量 である。
グレゴーリオ・リッチ = クルバストロ に 因んで その 名 がある。
gμν 時 空 の 計 量 テンソル 時 空 の 計 量 ンソル T_NAKA の 阿 房 ブログ-ウェブリブログ
T μν エネルギー 運 動 量 テンソル エネルギー・運動量 テンソル - Wikipedia
Gμν 〓 Rμν ー (1/2) Rgμν アインシュタイン テンソル - Wikipedia
∧ 宇 宙 定 数 ( cosmological constant ) は、アインシュタインの 重力場方程式 の 中に 現れ る 宇 宙 項 の 係 数。
宇宙定数 は スカラー 量 で、通常 Λ ( ラムダ ) と 書 き 表 される
k 〓 8πG / c 4 アインシュタイン の 重 力 定 数
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
★ アインシュタイン 方 程 式 の 導 出 Yahoo よ り
λμνωΓαβΛλθπ
外 参考 文献 道具としての 相対性理論 一 石 賢
わかつて来た 相対性理論 一 石 賢 ζηδRkνμλδρΨ∂
Rμν ー (1/2) Rgμν 〓 ( 8πG / c 4 ) T μν 1905 年 初 期 の 重 力 方 程 式
Gμν + ∧ gμν 〓 k Tμν 1916 年 宇 宙 項 を 追 加
ρ
● アインシュタイン 方 程 式 の 導 出 ( その ー 1 )wa
∂
Yahoo 検 索 資 料 よ り
出発点 リーマン 空 間 は d s2 = gμνd xμd xν (1) と 表される。
この リーマン 空 間 において ∇ωRkνμλ + ∇νRkμωλ + ∇μRkωνλ= 0 (2)
が 恒等的 に 成り立つ 。これは ビアンキ の 第 2 恒等式 と 呼ばれている。
Rkνμλ は リーマン・クリストッフェル の テンソルで
Rkνμλ =∂Γkμλ/∂xν - (3) と 計算 される。
�μ� は クリストッフェル の 記号 と 呼ばれ、
�μ� =12g�! �@gμ!@x� +@g�!@xμ−@gμ�@x! � (4)
∇! は 普通 の 微分 と 違い、共変微分 である。
ビアンキ の 第 2 恒等式 から∇μ �Rμ� −12Rgμ�� = 0 (5)
Rμ� はリーマン・クリストッフェル の テンソルを
縮約したもので、リッチテンソル と 呼ばれて いる。
R は リッチテンソル を さらに 縮 約 したもので、曲率 スカラー と 呼ばれている。
さて 流体力学 におけ るエネルギー 運動量 テンソ 2ル は、
Tμ� =� �vx �vy �vz�vx p + �v2x �vxvy �vxvz�vy �vxvy p +
�v2y �vyvz
�vz �vxvy �vyvz p + �v2z (6)
@Tμ�@xμ = 0 (7) が成り立つ。
それは例えば連続の方程式
@�@t+@�vx@x+@�vy@y+@�vz@z= 0 (8) である。 (�vx = ix で流れを表す。)
Tμ� = T�μ (9) で 対 称 である。
(5) は Gμ� = Rμ� −12Rgμ� (10) とおき、
∇μGμ� = 0 (11) とも 書ける。
Gμ� = G�μ (12) で 対称 である。
(7) はリーマン 空間版 で ∇μTμ� = 0 (13) と 表されるだろう。 もちろん
∇μ�Tμ� = 0 (14)
(11) と(14) を比較して Gμ� = �Tμ� (15)
と言えないだろうか。これは 物理的仮定 である。
これが アインシュタイン方程式 ( 宇宙項なしの。) である。
(15) の� の値は、ここでは詳しく述べないが、
ニュートン力学と照らし合わせて� =8�Gc4 (16)
アインシュタイン方程式は Gμ� =8�Gc4 Tμ� (17)
両辺にg μg � をかけて縮約すると
G =8�Gc4 T (18) 添え字 を 置き換えて Gμ� =8�Gc4 Tμ� (19)
ところで、物質 の ないところつまり からっぽ の 空 間 で の アインシュタイン 方程式 は
Tμ� = 0 (20) より Gμ� = 0 (21) となる。
つまり、 Gμ� = Rμ� −12Rgμ� = 0 (22)
gμ�Gμ� = gμ�Rμ� −12Rgμ�gμ� = 0 (23)
R��−12Rg�� = 0 (24)
R −12R��� = 0 (25)
R −12R · 4 = 0 (26)
−R = 0 (27)
R = 0 (28)
(28) を(22) に代入して Rμ� = 0 (29)
からっぽ の 空間 では リッチテンソル が 0 になることがわかった。
参考文献 1) 須 藤 靖「一般相対論」2016 年、日本評論社
2) 矢野健太郎「リーマン幾何学入門」1990 年、森北 出版株式会社
● アインシュタイン 方 程 式 の 導 出 ( その ー 2 )
わかつて来た 相対性理論 一 石 賢 よ り
このところ禁煙や宇宙についての記事ばかりで、女性読者は減る一方だろうなという自覚はあるのだが、
今日も懲りずに「一般相対性理論」の話。なるべくわかりやすく書いたつもりだけど。
この「道具としての相対性理論」の後半をこの2週間勉強してきた。重力によって空間が曲がるとか、
時間が遅くなるとかいうのが一般相対性理論であるが、どうしてそんなことが言えてしまうのか、
数学的にそういうことがどのように導かれるのかどうしても知りたかった。
この本の後半でこの理論が非常に高度な数学を使って説明されている。
1回では理解できず、結局2回読んだのであるが、1回目で40%、2回目で80%ほど理解できるようになった。
アインシュタインがたどった道筋でこの本の解説が進んでいるかどうかは知らないが、
この本では以下のようなシナリオで解説している。(数学がわからない読者でも、
なんとなく理解できるように自分の言葉で書いたつもり。)
1)「曲がった空間」についての数学的な表現を得るために、まず「斜交空間」の数学的な表現を紹介している。
私たちが高校の物理で習う空間は直交空間である。座標軸が斜めになっている斜交空間を純粋に
数学的に説明している。そしてベクトル、行列、テンソルなどのおさらいをする。
この本で説明しているテンソルとは具体的には4x4=16個の要素からなる行列の形をしていて、
それを1文字の「T」として表し、複数の物理量をまとめて表している。
また「T」はベクトルから別のベクトルへの変換を行うための「演算子」としての意味も持つ。
テンソルには共変成分、混合成分、反変成分を考えることができ、
それら3つには座標変換に対してテンソルの式で表現される関係性がある。
ここでテンソルという言葉をうまくイメージできない読者はとにかくそういう「もの」があると飲み込んでほしい。
2)次に斜交空間から別の斜交空間への変換について説明している。
空間上のすべての点において「座標軸が段階的に変化する角度で交わっている無数の連続した斜交空間」を
想定することで曲がった空間を表現するためである。
ここでは座標の変化が重要なポイントであるので、空間のそれぞれの座標において「微分」が行われ、
曲がった空間のそれぞれの点における数学的法則がテンソルの微分の形式で導かれる。
(きわめて曖昧な言い方で、数学的には正確ではない表現であるが。
この日記では数学を理解しない読者を想定するので、ご容赦を!)ここまでの説明は「あらゆる曲がった空間」に
対して適用されるため、数学的な表現としてはきわめて抽象的である。
この段階では相対性理論とは関係なく、数学的空間の説明をしているだけである。
3)曲がった空間の例として「リーマン空間」を紹介する。リーマン空間の数学的定義はとてもシンプルである。
この段階でも相対性理論とリーマン空間を結びつけているわけではなく、
単に数学的な表現としてリーマン空間を紹介しているにすぎない。
リーマン空間でテンソルの微分がどのように表現されるかを説明している。
(テンソルの共変微分)次に「空間の曲がりの程度(曲率)」を表すテンソルを導く。
それから「ビアンキの第1恒等式」、「ビアンキの第2恒等式」という有名な式が
リーマン空間上のテンソルに対して常に成り立つことを導く。
この段階でも、リーマン空間について数学的性質から導かれるテンソルの説明をしてるだけで、
相対性理論とは結び付けられていない。
4)リーマン空間上の曲率テンソルを縮約して得られる「リッチのテンソル」を導く。
これも空間の曲がり方を表すテンソルのひとつである。次に「リッチのテンソル」と
「ビアンキの第2恒等式」から「アインシュタインのテンソル」を導く。
ここでも相対性理論とは関係ない議論として進んでいる。
数学的な展開をしているだけである。 つまり重力によって空間が曲がるとかいう一般相対性理論の本質を
証明しているわけではない。
5)いったん「リーマン空間」を離れて重力と慣性質量、特殊相対性理論で紹介した「ミンコフスキー空間」の
説明にうつる。「ミンコフスキー空間」は3次元空間に時間の1次元を加えた4次元空間、
つまり「時空間」のことで、曲がった空間ではなく「真っ直ぐな時空間」である。
時間と空間をまとめて4次元として扱うことで、時間と空間を対等に扱うことができる。
次にこの4次元空間でエネルギーや速度、運動量などの物理量がどのように表現されるかを導く。
そしてエネルギーと運動量がまとめてひとつのテンソルとして表現されることがわかる。
最後にこのテンソルに対して「エネルギー・運動量テンソル保存の法則」が成り立つことを確認する。
6)4次元のリーマン空間での直線(測地線)について考える。
つまり曲がった時空間で直線はどのように数学的に表現されるかということ。
直線は2点を結ぶ最短距離となる線で、時空間が曲がっている場合は曲線となる。
その曲線(測地線)の方程式を求めるために変分法という手法を使う。
変分法とは簡単に言うと、2点間の積分路(曲線)をいくつか考えて、それらの積分路で積分した値の差を取って、
それが一番小さくなるような積分路(曲線)を探すものだ。
その結果得られる測地線の方程式は、リーマン空間内における質点の運動方程式でもある。
この運動方程式は計量テンソルの式として表現され、物体の質量の情報は計量テンソルの中に隠れている。
7)次に重力によって自由落下しているエレベーター(シンドラー社製ではないが)内の系と地上での系を考え、
その運動方程式から「計量テンソル」と「重力ポテンシャル」を導く。
計量テンソルは時空間の状態(曲がっているとか真っ直ぐとか)を反映しているのだが、
それが重力ポテンシャルによって影響があることが計算から導かれた式で確認できる。
(つまり重力が時空間を曲げるという予想が得られる。)
8)ここから一般相対性理論の核心である重力方程式の説明に入る。
重力質量と慣性質量が等しいとする「等価原理」そして、重力方程式が3つの条件を満たすことを前提とする。
3つの条件とは、1)一般座標系に対して、重力方程式はテンソルの形で書かれること。
2)重力方程式は計量テンソルの2階までの微分を含むこと、3)重力方程式の一方の式は、
エネルギー・運動量テンソルであること。などである。
そして重力方程式は「空間の曲がりを表現したテンソルの式=(左辺の原因となる)エネルギー・運動量テンソルの式」
という形で表現される。つまり、これまでにさんざん準備してきた4次元のリーマン空間でのテンソルを使った
数学的表現がこの式の左辺と右辺および3つの前提条件に現れる。
だからアインシュタインは一般相対性理論を証明したわけではなく、リーマン空間や重力方程式が満たす条件を
テンソルを含んだ式として表現し、時空間や重力の性質をそのようなものだと予想したにすぎない。
9)アインシュタインの重力方程式には抽象的な計量テンソルが10個も含まれた連立2階非線形偏微分方程式に
なるから、厳密な解を求めることはとても難しい。しかし、1)物体が球体で質量密度が一様、
2)時間的に質量密度は変動しない、3)原点から十分遠い場合には空間は平坦(ミンコフスキー空間)になる、
という3つの条件をつけると、厳密な解の1つを求めることができる。
この解を発見者の名前にちなんで「シュヴァルツシルトの厳密解」という。
この特殊な条件で計算を進めると空間内に「特異点」が存在することが導かれる。
この球体の中心から半径aである球面上で時間や空間がゼロになってしまう。
そしてその球面の内部が、通常私達が「ブラックホール」と呼んでいるものであることがわかる。
つまりブラックホールの存在が予想されたわけだ。
この本に書かれていることは、ここまでである。
僕が2回読んで80%しか理解できなかったというのは、途中で展開しているテンソルの計算が非常に複雑で、
ついていけなかった箇所があったからである。けれども全体的にどのようなことをしているのかはわかっていたので
最後まで読むことができた。数学的に宇宙論を理解するということが、どういうものであるのかが
感覚的にわかったのが一番よかったと思う。アインシュタインは数学を使って宇宙のあり様を「予想」したのであって
「証明」したのではないことがよくわかった。
ミンコフスキー空間だとかリーマン空間だとかユークリッド空間だとかヒルベルト空間だとか。。。
この分野ではいろいろな空間の名前がでてくるが、そのような空間がそれぞれ別個に存在するわけではない。
現実世界の空間はあくまで1つなのだけど、それを数学的にどのように解釈し定義付けして見るかによって
別の名前で呼んでいるだけである。たいていその発見者の名前をつけるわけだ。
とりあえず、この本はおしまいということにして、次は「一般相対性理論:ディラック著」に挑戦しよう。
以前 たった4ページで 挫折した 本だ。
● アインシュタイン 方 程 式 の 導 出 ( その ー 3 )
道具 としての 相対性理論 一 石 賢 よ り

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
![]()
![]() np - 77
np - 77





 よ り
よ り 