E = m c² 　の 証 明　 展 開 式　　　 　　　

　sub - 10
H 25 - 7 Up

参考　文献　　　電 磁 気 学　二村忠元　著　　恩 師　東北大教授　　相対性理論　内山龍雄　訳　　理論電磁気学　砂川重信　著　　np - 125
　　　
対性理論　佐藤健二　著　　相対性理論　佐藤勝彦　著　　相対性理論　竹内　淳　著　アインシュタイン の 世 界 　Internet　 Surfiing

　　アインシュタイン の フアン のひとり 、 E  =  m c ² こんな 式がどうして導きだされるのか 不思議 に思っておりました。

　　たま〜、卒業後　昭和 51年 に 　二村先生 の 還 暦 祝 賀 会 をかねて 同期会 の 一泊旅行 がありました。

　　その際に 、先生から 記 念 としてこの 電 磁 気 学の 本 をいただきました。

　　この 参考書 の 中 に 　アインシュタイン の 相対性原理 関 係 について詳しく 　解 説 　されていました。

　　とても難しい内容でなかなか理解できませんでした。繰り返し読んでいるうちに少しづつ 理 解 できました。

　　　　メ モ がわり に 記 録 　して 残 す ことにしました。　 　 　　　二 村　研 究 室　　Yahoo　　　二 村 教 授　画 像　　　東北大


　　 　▼　　特 殊 相 対 性理 論　は アインシュタイン が 1905年 に 発 表 した 電 磁 気 学 の 理 論 です。

　　19 世紀 まではニュートン力学で、世界の物理学者の中に��　物理学 にはこれから 見出すものはもうない��

　　という方がおられたそうです。　ところが、　アインシュタイン　の 特殊相対性　理 論 の 発 表 で

　　　　物 理 学、電 磁 気 学 の 世界 は 新しい時代 を 迎えました。　

　アインシュタイン　　　　　　　1922 年　東北大　来 校


　　　アインシュタイン が 特殊相対性 理 論 の構 築 ができたのも 大昔から世界中 の 学 者 が長い年月にわたり

　　築きあげた 業 績 を 土 台 に 天才 アインシュタイン が アンカー となったような気がします。

　　陸上競技、リレー の バトンタッチ でいえば　→　→　ニュートン → マイケルソン → ローレンツ → アインシュタイン

　　　　　　となりましょうか　

　　　特 に 、1887年　に行われた　　　★　　『　マイケルソン ・ モーリー　の 実 験　』　　もその一つです

　　これまで、世界の物理学者　科学者は 光 は エーテル という 物 質 を 媒 体 として 伝 搬 すると考えていました。

　　ところがこの実験結果 エーテル の 存在 は 認められなかった。 エーテル 理 論 の 否 定 となりました。

　　同時に、「第二次科学革命の端緒」 と 評されている。 マイケルソンは、この業績により1907年に　ノーベル賞　受賞


　　　　　更 に 、　★　　ローレンツ 変 換　は　2 つ の 慣 性 系 の 間 の 座 標

　　（時間座標と空間座標） を結びつける 線形変換 で、電磁気学 と 古典力学 間 の 矛盾 を 回避するために 、

　　アイルランド の ジョセフ・ラーモア（1897年）と オランダ の ヘンドリック・ローレンツ（1899年、1904年）により提案された。

　 アインシュタイン が 特殊 相対性 理 論 （1905年）を 構 築したときには、慣 性 系

　　 間 に 許される 変換公式 として、理 論 の 基 礎 を 形 成 した。　　 Wikipedia より


　　　　●　　　Michelson - Morley　の 実 験　　　　　　　

　　　　　　　　　　　　　　詳しくは 前 掲　H P　　　 (　こちら を 参 照 ください　)

　　　　　　　　　　　　　　　　　ここでは 、 概 要 を 記 し ます

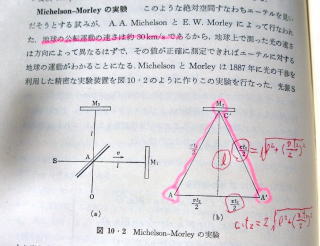
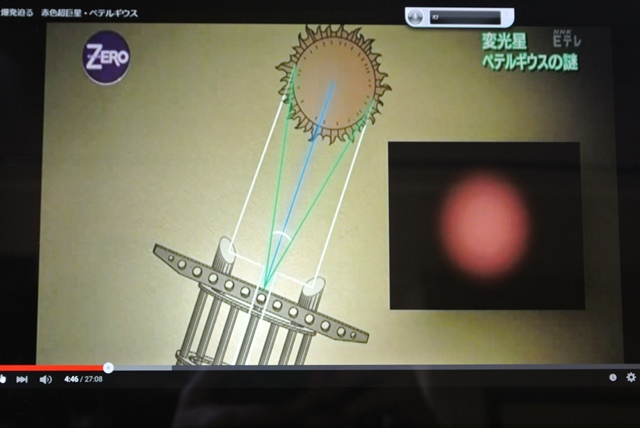
　　　　　　　　実 験 装 置

　　　　　　　　　　　　　　　　　　　　　　　　　


　　　　　　　　　　　　　　　

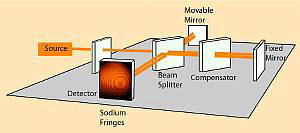
　　　　　　　　　　　　　　　マイケルソン　　　　　　　　　　　　　　実 験 装 置 の イラスト

　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　 Youtube では　音 声　つき の 解 説 があります


　　この実験装置は膨大で地下室に水 銀 のプールを作りそこに大理石 のテーブルを浮かべて

　　その上に測定装置を設置してある。精密な測定をするため、振動　室内の光　空気の乱れを

　　避ける配慮がされている。尚、水 銀に浮かべてあるので測定装置の方向が容易に変えられる。　

　　　　　　　　　　　　　　水銀の比重　　13.6　　　　大理石の比重　　2.5〜2.9

　　　　　　　　　　　　　


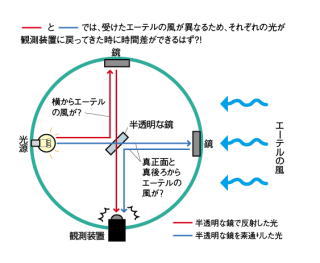
　　　　　　　　　　　　　　　『　実 験 装 置の 動 作 説 明　』

　　　　　イラスト 図　中央 に 半透明 の ミラー　M₀ を 置 く

　　　　　X 軸　左に　ミラー　M₁　を 置 く　　　　( X 軸 は 地 球 の 公 転 方 向 とする )

　　　　　Y 軸　上に　ミラー　M₂　を 置 く

　　　　　ミラー　間 の 距 離　　M₀ 〜 M₁　と　　M₀ 〜 M₂　　は共に等しく　　lm　　とする

　　　　　光 の 速 度 　　c = 30 万 km / s 　　　　地 球 公 転 の 速 度　 v = 30 km / s



　　　　　　　　　　　　　　　　

　　　　　　　　　　　　電 磁 気 学　二村忠元　著　(東北大 教授)　　より　　　一部　スキップ　短 縮

　　絶対空間すなはちエーテルを見出そうとする試みが、　Michelson と Morleyによって行われた。

　　地球の公転速度は30km/sであるから、地球上で測った光の速さは方向によって異なるはずで、

　　その値が正確に測定できれば エーテル に対する 地 球 の 運 動 がわかることになる。

　　Michelson と Morley は1887年に 光 の 干渉を利用したこの精密な 実験装置 で 実験 を行った。

　　光源より出た光を半透明な鏡を通して同方向におかれた鏡 M₁ との間を往復させ、またこれと垂直に

　　半透明な鏡で反射される光を等距離におかれた鏡 M₂ との間に往復させて、両 光線を観測点からみて

　　その干渉を観測した。エーテルに対する 地 球 の速さを v　とすれぱ゛、地 球 の運動方向および

　　その反対方向における地球上の光の速度はそれぞれ c - v　、c + v となるから、　M₀ M₁ がこの方向に

　　　　おかれていれば、光 が 往復する 時間　　t₁　 は

　　　　　　　　　　　t₁ =  l / (c - v) + l / (c + v)  =  2c l / (c² - v²)  =  (2 l /c) / (1 - v² / c²)

　　　　　　またこれと直角方向については、 M₀ M₂の 往復時間　 t₂　 は

　　　　　　　　　　　t₂  =  2 l/ √(c² - v²)  =  (2 l /c) / √(1 - v² / c²)

　　　　　　従って、到着時間 の 差　　　　�冲  =  t₁ - t₂  ≒  ( l / c ) (v / c) ² = l v ² / c ³

　　このように 光 の到着時間が異なるために、両光線の間には位相差生じ干渉縞ができるはずである。

　
　　　　　　　　　　　　　　　　　

　
　　　　　　　


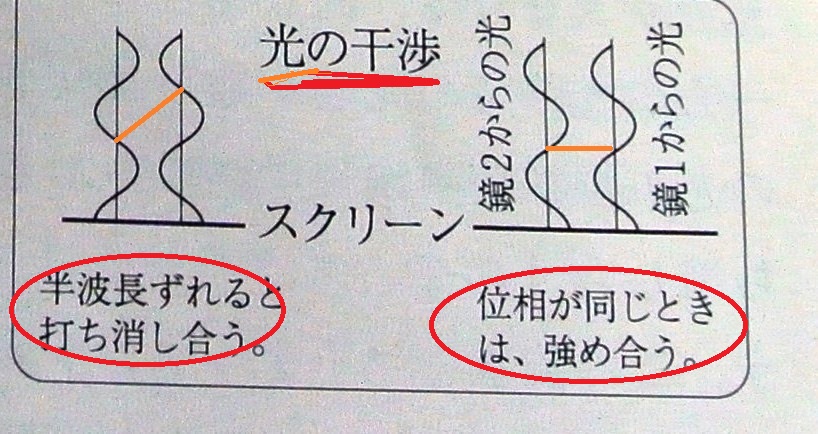
　　　　　　結果は予想に反して 位 相 差 のないことが 確 認 された。

　　　　　　すなわちエーテル に対する 地 球 の 運 動 はまったく 見いだされなかった。

　　　　　　　　　　　　　エーテル 説 の 否 定 となりました。


　　　　　　　　　　　　　　　


　　　　●　　　ローレンツ　　収　縮　

　　Michelson . Morley の実験において地球 の公転方向に走る光 と これに垂直に走る光 には

　　　同 じ 距 離 を 往 復 させたとき、相対速度 で計算すると 時 間 差 を生じることになる。

　　　　　　　　公転方向 に 往復させたときの 時 間　　t₁　は

　　　　　　　t₁  =  l / (c - v) + l / (c + v)  =  2c l / (c² - v²)  =  (2 l /c) / ( 1 - v² / c<sup>2 ₎

　　　　　　　　　　　垂直方向 に往復させたときの 時 間　　t₂　は</sup>

　　　　　　　　　　　　　　t₂  =  2 l/ √(c² - v²)  =  (2 l /c) / √(1 - v² / c²)

　　　　　　　　　到着時間 の 差　は　　　　�冲  =  t₁ - t₂  ≒  ( l / c ) (v / c) ²　＝　l v ² / c ³

　　　　　　　　　　　　ところが 実験結果 では 時 間 差 は 確 認 できなかった。

　　　　　　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　　　　　　★　　　追 記　　　　�冲  =  t₁ - t₂  ≒  ( l / c ) (v / c) ²　＝　l v ² / c ³

　　　　　　　　　　　　この　近 似 式 が どうしても 導 け ません でした

　　　　　　その後　相対性理論　竹内　淳　著　　著書 の 中 に　　√ ( 1 - a ) 　≒　　1 - a / 2　が ありました

　　　　　　　　　　　この　近似式 の 公式 を 使うと 簡 単 に 導 く ことが できました　　納 得

　　　　　　　　　　　地球の公転速度 v は 30 �q　光の速度 c は 30万 �q　(v / c) ² は

　　　　　　　　　　　1万分 の 1　の　２ 乗　で　1　億分 の １　となり　1　に比べると　はるかに小さい　　無 視　する　

　　　　　　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−


　　　　　　ローレンツ　はこれをうけて　すべの物体は エーテル に対して運動することによって、

　　　　　　その運動方向に　√(1 - v² / c²) の割合だけ 長さが縮まる という大胆な仮定を行った。

　　　　　　この短縮を認めると　t₁ における　l は　l √(1 - v² / c²) と 置き換えられるから

　　　　　　　　　　　　　　t₁ =  2 l　/ √(c² - v²)　となり　　　t₂ 　と 等しくなります

　　　　　　　　　　　　従って、　　�冲 =  0　　すなわち 位 相 差はなくなる。

　　　　　　　　　　　　　この長さの 収 縮 を　ローレンツ　収 縮　という。

　　　　　ローレンツ はこの長さの収縮の原因を、物質の電子間の力がエーテルに対する運動状態に

　　　　　　よって変化すると説明したけれども、その理論には多くの特殊な仮定が含まれていて、

　　　　　　　　　その 理 論 的 根 拠 はあまり満足なものではなかったという。

　　　　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
　

　　　　　　★　　追 記　　ローレンツ　収 縮　　√(　1 - v ² / c ² )　 に つ い て　　　2015−11−19

　　　　　　この　式がどのように導いたのか分かりませんが多分マイケルソンの実験で

　　　　　　時間差 が 認められなかったこと　時間差　＝　０　　となることを　説明するために　逆算的に　求めたか

　　　　　　　後 に　　√( 1 - v ² / c ² ) 　≒　1 - v ² / 2 c ² 　　と　近 似 式 で 表せる　ことを　知　りました

　　　　　　　　テイラー　展 開　　f ( x ) = f ( 0 ) + f ゜( 0 ) x + f�� ( 0 ) x 2 + ・ ・ ・ ・

　　　　　　　　　　　 x =　√(　1 - v ² / c ² )　を 代 入 して　第 2 項 まで 拾 う と この 近 似 が 得られる

　　　　　　　　◆　　　他 の　説 明 方 法　　　　√ ( 1 - a ) ≒　1 - a / 2　　　　　

　　　　　　　　　　　　a　　　　　　　0　　　　　　　0.01　　　　　　0.1　　　　　　0.2

　　　　　　　　　　√( 1 - a ) 　　1　　　　　　　0.9949　　　　0.9486　　　　0.8944

　　　　　　　　　　1 - a / 2 　　　1　　　　　　　0.995　　　　 0.95　　　　　　0.9

　　　　　　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−


　　 　 ●　　　　E　=　m c ²　　の　式　の 　誘 導 　展 開 式　 　【 エネルギー と　質 量 の 等 価 性 】

　　　　　　　この式 の 誘 導 にあたって、前提条件 を拾って挙げ イメージ 的 に 理 解 しやすく　します。


　　　　　　　　　　　▼　　ガリレイ 変 換

　　　　　　　　　　　　　　　　　　　　　　

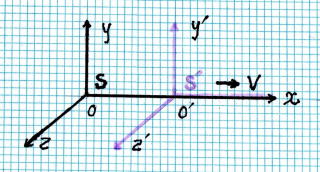
　　上図のような直角座標軸をもつ二つの慣性系　 S 、S´　をとり、これらの相対する座標軸は互いに

　　　　　　　　　　　平行で、S´は　S 系の　x 　軸上を正方向に一定速度　v で動くものとする。

　　　　　　　このときある物理現象の起こった位置と時間を、S´および　S 系で測った値を、それぞれ

　　　　　　　　　　　　　　　　　x 、 y　、z 、 t　　 および　 x ´、 y ´　、 z ´ 、 t ´ 　　と　し、

　　　　　　　時間は両系に共通な絶対不変量と考え、またある時刻　で両座標系の原点が一致しているものとすれば、

　　　　　　　　　　　　　　　　　 x ´ =  x - vt 、 y ´ =  y 　、 z ´ =  z 、  t ´=  t　　　　となる。

　　　　　　　　　　　　　　　　　　　　　　このような 変 換 を　ガリレイ 変 換という



　　　　　　　　　　　▼　　ローレンツ 変 換　、　ローレンツ　収 縮　、　局 所 時

　　　　　　マイケルソン の 実 験 において 地 球 の 公転方向 を走る 光 とこれに 垂 直 な 方向 を

　　　　　　等距離 走る 光 のを 相対速度 で計算 すると 時 間 差 が生じるはずである。

　　　　　　時間差 があれば、両 光線 間 には 干 渉 縞 が 生じるはずである。

　　　　　　ところが、実験結果では 干 渉 縞 は 観 測 されなかった。 時 間 差 が 認められなかった。

　　　　　　　　　従って、光 が エーテル によって伝搬するという説 が 否 定されました。

　　　　　　　　　
　　　　　　ローレンツは マイケルソンの 実 験 を 説 明 するために、 ガリレイ 変 換 を変更して

　　　　　　ローレンツ 収 縮　と　局所時　という考え方を入れて、いわゆる　ローレンツ変 換、すなわち

　　　　　　　　　　　　　　　 x´　=  (x - v t) / √(1 - v² / c²)　　 　　y´ =  y 　 、 　z´ =  z

　　　　　　　　　　　　　　　 t´ =  (t - v x / c²) / √(1 - v² / c²)

　　　　　　を用いて、絶対静止系　S と エーテル に対する運動系　S´において、厳 密 に　の方程式が

　　　　　　　　　成り立つようにすることができることを、 1904 年 に示した。


　　　　　　アインシュタイン　は ローレンツ　の 理 論 を深く考 察 して、 特殊相対性 理論 を 提 案 した。

　　　　　　　　　　　　　　　　　翌 1905 年 のことで 年 齢 26 歳 であった。



　　　　　　　　　　　▼　　ローレンツ変 換　の 誘 導

　　　　　　　　　　ローレンツ 変 換　　　　x ´　= (x - vt) / √(1 - v² / c²)　　 　　y ´= y 　 、 　z ´= z　　　　 ( 0 1)　

　　　　　　　　　　　　　　　　　　　　　　　　　　　 　t´ =  (t - vt) / √(1 - v² / c²)　　　　　　　　　　　　　　　　　　　　　　 ( 0 2 )

　　　　　　　　　　　は　相対性原理　および　光速度不変の原理　から　導かれます。

　　二つの惰性系　S および　S´　が、　t = t ´ において両系の原点が一致し、S´系 が S 系 に対して

　　　　　　　　　　　　　x 　軸上 を一定速度　v　 で 動いている とする。

　　いまこの原点の一致した瞬間に両原点から光の信号が出されたものとすれば、この 波 面 は

　　光速度不変の原理によって、S´および　S 系　において、それぞれ次のような 球 面 で表される。

　　　　　　　　　　　　　x² + y² + z² - c²t²  =  0　　　　　　　　　　　　　　　(0 3)

　　　　　　　　　　　　　　x´²　+　y´²　＋z´²　- c² t´²  =  0　　　　　　　　　(0 4 )

　　　　　　　　　　　四 次 元 時 空　　x² + y² + z² = c² t²　球表面の方程式　半径 = c t　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　これら 二つの 惰性系 の 間 の 変換法則 は一般に 線 形 ( 一次式 直線 ) でなくてはならない。

　　　　　　　　　なぜなら、もしそれが 非線形 ( 直線でない　二次式　y = a x 2 + b 　三次式　等 ) であるなせらば、

　　　　　　　　　その変換によって上しきの二次形式 を保つことが　できないからである。


　　　　　　　　　従って上の一方の式から他方が導かれるために、座標返還式を

　　　　　　　　　　　　　次のような線 形 の返還式で表す、　　

、 　　　　　　　　　　　　　　　　　　　x´　=α (x - v t) 　、　 　　y´= βy = y　 、 　z´= γz = z 、　　　t´= δx + εt 　　　( 0 5 )

　　　　　　　　　　 これらを　( 0 4 )　式に入れ、　( 0 3)　式 と 比 較 して

　　　　　　　　　　v α² + c²δε = 0 、　　β = γ = 1 、　　c²ε² - v²α² = c²β² 　、　α² - c²δ² = β²　　　( 0 6 )　　を 得 る。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　↓　　　　　　　　　　　　　　　　　　　　↓
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 c²ε² - v²α² - c ²= 0　　　　α² - c²δ² - 1 = 0

　　　　補　足　　慣性系　K´ は　速 さ　V で x 軸方向 にのみに　移 動 してい るので　　y ´ 　= 　y 　　 z ´ 　=　 z 　　　β　 = 　γ 　=　 1


　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

　　　　●　　　追　記　　　(6)　式　の　導 出　が　できない 　　　　　　　●　　2015-12-19 　　　上 記　補 足　で　理 解　できました


　　　　　　　　　　　この　変 換　導 出　は　50年 前　出版 された　砂川重信　著　理論電磁気学　によるもの

　　　　　　　　　　　　最近　出版 された　竹内　淳　著　　高校数学でわかる　相対性理論　では

　　　　　　　　　　　　具体的 に　丁寧 に　説 明　されているので　理 解　できました

　　　　　　　　　　　　　　　　Copy 　しておきました　　　　　　2015−12−12　追　記

　　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−ーーーーーーーーーーーーーーー

　　　　　　　　　　　　いま　　α = A β 、　　δ = D β 　、　　ε = E β　　とおくと　　　( 0 6 )　　は

　　　　　　　　　　　　　　　　　　　　　　　　 A² = - (c² / v) D E　　　　　　　　　( 0 7 )

　　　　　　　　　　　　　　　　　　　　　　 c² E² - v² A² = C²　　　　 　　 　 ( 0 8 )

　　　　　　　　　　　　　　　　　　　　　　 A²- c² D² = 1　　　　　　　　　　　　( 0 9 )

　　　　　　　　　　　　　　　( 0 7 ) 　式 を　 　( 0 8)　、　( 0 9 )　に入れて

　　　　　　　　　　　　　　　　　　　　　　 　E (E + v D) = 1

　　　　　　　　　　　　　　　　　　　　　　　　　D (E + v D) = - v / c² 　　　　　　　( 1 0 )

　　　　　　　　　　　　　　　これから　　　D = - (v / c²) E　　　　　　　　　　　　( 1 1 )

　　　　　　　　　　　　　　　　( 1 1 )　式を　 (1 0 )　に入れて

　　　　　　　　　　　　　　　　　　　　　　　E² (1 - v² / c²)  =  1 　　すなわち　　E  =  1 / √(1 - v² / c²)　　　　　( 1 2 )

　　　　　　　　　　　　　　　　これと　 ( 1 1 )　 　よ り　　　　D  = - (v / c2) / √(1 - v² / c²)　　　　　　　　　　　　　　　( 1 3)

　　　　　　　　　　　　　　　　従って　　( 0 7 )　より　

　　　　　　　　　　　　　　　　　　　　　　　A² = 1 / (1 - v² / c²) 　　すなわち　　A  =  1 / √(1 - v² / c²)　　　 ( 1 4 )

　　　　　　　　　　　　　　ここて゛　( 1 2 )　、 ( 1 4 )　などで 正 号 をとった理由は、　v = 0 　のとき　S系　と　、S´系　が

　　　　　　　　　一致 しなくてはならないからである。　(E²　および A²　の平方根には数学的 には + -二つ　あります)

　　　　　　　　　　　　　　　　また　　v = 0　　のとき　　β = 1　　γ = 1　　となるから、　すべての係数が決まったことになる。

　　　　　　　　　　　　　　　すなわち　　( 0 5 )　式　は　　　

　　　　　　　　　　　　　　　　　　　　　　x ´　=  (x - v t) / √(1 - v² / c²)　　 　　y ´=  y 　 、 　z ´=  z　　　　 ( 1 5)　

　　　　　　　　　　　　　　　　　　　　　　　 　t´ 　=  (t - v x / c²) / √(1 - v² / c²)　　　　　　　　　　　　　　　  　　 ( 1 6 )

　　　　　　　　　　　　　　　　　と な る。　　　すなわち　　　　【ローレンツ　変 換 】　　である。

　　　　　　　　　　　　　　　( 以上、この　ローレンツ　変換 の 誘 導　は　電磁気学　より　　原文 のまま )


　　　　　　　　　　　　　　(この　式　の 誘 導　展 開 にあたって　私の 感 想 )

　　　　　　　　　　最終目的 の 式 に 到 達 するたるために　トリッキー　な 変 数 変 換 を行っておりますが、

　　　　　　　　　　この　手 法 は 三次方程式 の 解 の 公 式 を 導 く 手 法 と 似ております。

　　　　　　　　　　三次方程式の解の公式の誘導もトリッキーな変数変換を繰り返して三次方程式の一般式を

　　　　　　　　　　二次方程式に化 けさせて二次方程式の解(分解方程式) を利用して、この後逆変数変換 をして

　　　　　　　　　　　　　　　　　三次方程式の解を導くという手法です。

　　　　　　　　　世 の 学者 はこのような 手品 的、マジック 的 な 手 法 をどうして　見出せるのか不思議に思えました。　

　　　　　　　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−


　　　　　　　　　　　　▼　　相 対 速 度 　と　合 成 速 度　　　　　

　いま一定速度をもってx 軸 に平行に運動している質点を考え、その　S および　S´系における速さを u および u´ とする。

　　　　　　　　　　　　ガリレイ変換においては　　　　　　u = u´ + v　　　　(1 7 )　　　　相 対 速 度　　　であるが

　　　　　相対理論 ではこうならない。　　S´系 において　t´ = 0 における質点の座標を　x ´　とすれば、S´における　

　　　　　　　　　質点の運動は、　x ´=  u´ t´ + x₀´　で表せられる。

　　この式の　x ´、 t´　をローレンツ　変換によって　x . t で表し、その結果が S系におれる質点の運動の式　x = u t + x₀　

　　　　　　　　　と　一致するためには、簡単な計算の結果　　　u = (u´ + v) / (1 + u´v / c²)　　　　( 1 8 )

　　　　　　　　　　　　　　とならねばならないことがわかる。　　　この 式 を　　　合 成 速 度　　　という

　　　　特に　　v 　および　 u　が　c　 に比べて十分 小さいときに　(1 8 )　式の分母は　1　となるので　( 1 7 )　と 一致する

　　　　　　　なお、　(1 8 )　式　を 変 形 して　　　　u = c [ 1 - (1 - u´/c) (1 - v / c) / (1 + u´v / c²) ]

　　　　　　　となるから、光 速度 より小さい 2個 の速度 (u´、v ＜c) の 合成は常に　より小さい速度(u ＜c) となる。

　　　　　　　特に、　u´　と　v 　のどちらか一方または両者が　c　に等しいときは　u = c　となる。

　　　　　　　　　　　結 局 、光速度　c　より　速い速度　をもつ 質 点 の 存 在 が　否 定 される。

　　　　　　　　　　　相 対 速 度　と　合 成速 度　　グラフ　に　描 い て みました


　　　　　　　　 　　　　　　　　　　　　　　　

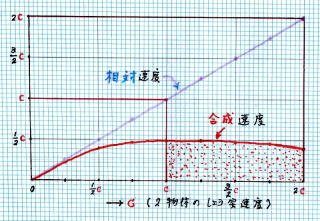
　　　　　　　　　　　　　　　　　　　　　　　　　　　グ ラ フ の 説 明　　　　( 縦 軸　目 盛　に 誤 記 あり　2 倍　してください )

　　　　　　　　　　　　　　　ヨ コ　軸　、　タ テ　軸　　　光 速 度　c 　の 単 位 　( 30万 km / s )

　　　　　　　　　　　　　　　ヨ コ　軸　は　2 物 体 の　衝 突 速度

　　　　　　　　　　　　　　　タ テ 軸　は　相 対 速 度　と 合 成 速 度

　　　　　　　　　　　　　　　赤　色　塗りつぶし　部 分　は　光 速 度 より速い 物 体 は 存在しない ことを 意 味 する

　　　　　　　　　　　例　　　　時速　100 km　の　自動車 が 正面衝突 するとき、

　　　　　　　　　　　　　　　相対速度　= 10 km + 100 km = 200 km = 合成速度

　　　　　　　　　　　　　　　　　時速　500 km の リニャーカー　秒速　8 km の　ロケット　の　正面衝突 においても

　　　　　　　　　　　　　　　相対速度　=　合成速度　　である

　　　　　　　　　　　　　　　グラフ　から　わかるように　光速度　の　1/4 以下　では

　　　　　　　　　　　　　　　　　　　　相対速度　=　合成速度　　である

　　　　　　　　　　　　　　　なお　、　光速度　の　30万 km/s　で 衝 突　するとき

　　　　　　　　　　　　　　　　　　　　相対速度　=　(c + c) = 2 c

　　　　　　　　　　　　　　　　　　　　合成速度　=　(c + c) / ( 1 + c.c / c² ) = 2 c / 2 = c

　　　　　　　　　　　　　　 また　、　光速度　の　2 倍　60万 km/s　で 衝 突　するとき

　　　　　　　　　　　　　　　　　　　　相対速度　=　(2c + 2c) = 4 c

　　　　　　　　　　　　　　　　　　　　合成速度　=　(2c + 2c) / ( 1 + 2c .2c / c² ) = 4 c / (1 + 4) = 4c / 5 = 0.8 c

　　　　　　　　　　　　　　結 局　、　光速度 より 速い 速 度 は この 宇 宙 には 存 在 しない ことを 示 し ます。

　　　　　　　　　　地 球 から遠くはなれた星の距離を 何万光年 と表現するのも、この　c = 30万 km/s で産出される。

　　　　　　−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−


　　★　　以上の 予備知識 をもとに 本 題　の　【 E  =  m c ² 　の　転 回 式　の　誘 導 】　とします　


　学生時代 、二村先生の電磁気学の講義 をサボッテて、映画を見たり、マージャンをしたりして遊びまくっておりました

　　　　　　　　　　　　80才 を 過ぎた今 頃 、罪 滅 ぼし に 勉 強 しなおしております


　相対性原理によると、すべての物理法則 が ローレンツ 変 換 に対して、不変すなわち 共変的 でなければならない。

　力学系における　Newton　の運動方程式をみると、Newton　の方程式はガリレイ変換に対しては共変的あったが、

　ローレンツ 変換 に対してはそうでない。　従ってこのローレンツ変換に対しても、運動法手式が共変的であるように、

　すなわち 相対性原理 が成り立つように 理 論 を 新しく組み立てる 要求 が生じた。

　さて、　古典力学 における　Newton　の運動 の法則 を改めて考察すれば、これは次の 3っの法則 よりできている。

　　　(1)　独立した 1個 の質点 は、静止しつづけるか 道速度 で 運 動 しつづける。

　　　(2)　2 個 の 質点 が 運 動 しているとき、その加速度　αの比は常に一定で、この質点系 に 固 有 のものである。

　この比を二つの質点の質量の比といい、第一の質点の質量を単位とするとき、- (α₁/α₂) を第二の質点の質量という。

　　　 (3)　質点 の 質量 と 加速度 との 積 を、その質点に働 く 力 という。

　　　　　　　　　　　　　　　　すなわち　　m α = m ( dv / d)t　 = 　F

　上の法則　は、これらの 法 則 が成立する 座標系 を 約束したものであって、いまわれわれが考察としている

　ローレンツ 変換 もこのような 座標系 すなわち 惰性系 の 範 囲 を出るものでないから 問題ない。

　しかし法則　(2) (3) は 、 については、質量 と 力 を 最初 に このように 数量的 に 定義することができるであろうか

　このことについては、Newton　の運動方程式は質点の速度が光速度　c に比べて小さいときのみ成り立つものであって

　その速度が　c に近づくと、　すなわち　β = v / cが 1 に近づくと当然これが変更されなければならないということを

　考えても、また ガリレイ 変換 では　t´ = t　が示すように、これを スカラー量 としていたのであるが、

　相対論的な時空間つまり ミンコスキー 空 間 おいては、時 間　t　はローレンツ変換 では スカラー量 ではないという

　ことなどから考えても、最初から質量 と 力 をこのように分離して定義することは相対性理論 では 困 難 であることが

　予想される。　そこで、われわれはこの代わりに、質量 と 運動量 を 力学 の基本的な量 と考えて、出発することにする

　すなわち、種々の質点が作用しあっている力学系を記述する基本的な法則として、系を構成する質点の質量の総和

　　ならびに　運動量の総和 について 保存則 が 成り立つ ものとするのである。

　そうするとこれらの 保存則 が 互いに ローレンツ変換 で結ばれるすべての 惰性系において 満足するためには　

　Newton　の力 学 の場合とは違って、　質 量 は一般に速 さ によって その値 が変 更 されなくてはならない。

　　　　　　　　　
　この質量がどのように変更されるかを見るために、2個の同一な完全弾性球が正面衝突する場合の質量と運動量の

　　保存則について考察してみよう。

　惰性座標系　S´と、この　x´軸方向に　- v なる速さで移動する惰性系　S をとり、S´系 のx´ 軸上を 2個 の粒子が

　+ u´ と - u´ の 速さ で運動 し、衝突 し、はね返る ものとする。

　完全男性球 であるから、衝突した瞬間には 両球 は静止するが、その後ただちに前と同じ 速度で反対方向 に運動 を

　続ける はずである。　さらに　S 系　における 2 粒子 の衝突前の速度をそれぞれ　u₁ u₂　質 量　を　 m₁ m₂ 　とし、

　S´系に対して静止しているるとき (たとえば衝突の瞬間) すなわち S系では速度 v をもっているときの全質量を M とする

　S系 でみた 質量 と 運動量 の 保 存 は
　　　
　　　　　　　　m₁  +  m₂　 =　 M 　、　　m₁ u₁  +  m₂ u₂　 =　 M ・ v　　　　　　　　　　　　　　　　　　　　　　 ( 19 )

　ここに　　u₁ u₂ 　は　　　( 1 8 )　の 速度合成 の式 を用いて、

　　　　　　　u₁　 = 　( u´ + v) / (1 + u´ v / c²)　　、　 u₂=　 (- u´ + v) / (1- u´v / c²)　　(20 )　　

　となるから、　　( 19 ) 　より　M 　を消去し、これに　(20 )　を用いて、　m₁　と　の　m₂ 　比 を 求めると

　　　　　　　m₁ / m₂　 =　 (1 + u´ v / c²) / (1 - u´ v / c²)　　　　　　　　　　　　　　　　　　　　　( 21 )

　さらに　( 20 )　より

　　　　　　　(1 - u₁²) (1 + u´v / c2) 　= 　(1 - u₂² / c²)

　　　　　　　(1 - u´v / c²)　 =　 (1 - u´² / c²) (1 - v² / c²)

　なる関係が得られるから、これを用いて　( 21 )　は

　　　　　　　m₁ / m₂ = 　√(1 - u₂² / c²) / √(1 - u₁² / c²)　　　　　　　　　　　　　　　　　　　( 22 )

　となる、この　2個の粒子はともに静止しているときには同一の質量をもつはずで、これを　m₀ とすれば、

　粒子が速さ　u　をもつときの質量　m　は上式に従って　　√(1 - u² / c²)　　に逆比例するから

　　　　　　　m　 = 　m₀ / √(1 - u² / c²) 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　( 23 )

　と書くことができる。　この　を 静止質量 という。　上式からわかるように、　

　　　　　　　u ≪ c　のときは　　m　 ≒ 　m₀　　、　　u　　が　 c 　に 近づくにつれて 質 量 は　∞　に近づく



◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆














ここで、挿 絵 的 に　[　 物 体 の 　質 量 ・ 長 さ　と　移 動 速 度　の関 係 　] を　グラフ　にしてみます

　　　　　　　　　　　　　　　　　　　M 　= 　M₀ / √(1 - v² / c²)

　　　　　　　　　　　　　　　　　　　L 　 = 　L₀ √(1 - v² / c²)　　　　ローレンツ 収 縮

　　　　 　　　　　　　　　　

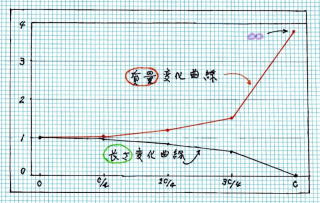
　前 掲 、　相対 速度　と　合成速度　の　グラフ　と　同 様 に　物 体 の 移動速度　が　光速度　1 / 4 以下 では

　　　　　　　　　　　　　　　　　M　 ≒　 M₀ 　　　　　　　　L 　≒ 　L₀　　　である

　　　　　　　　　　　光 速度　の　1 / 4 　あたりが　古 典 物 理 学　との　分かれ目　のようです　　

　　　　　　本 論　小 休 止　しました　　　　再 開　します

　◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆


　　　最 後 に、　運 動 量 について 考 察 する。　 W　=　 E　 = 　m c²　の　式 の　 誘 導

　　　　　　
　　　　　　::S 系　において 質 点 の 速 度　u　の 各成分 を　　u_x、 u_{y 、} u_z　　とすれば、その 運動量　の 各成分 は

　　　　　　　p_x = m₀ u_x / √( 1 - u² / c² ) 　　、　p_y = m₀ u_y / √ ( 1 - u² / c² )　　、　 p_z = m₀ u_z/ √( 1 - u² / c² ) 　　( 24 )

　　　　で表される。　この運動量は自由な質点の場合は一定で、力が働けば変化するはずである。

　　　　そして この運動量 の 時間的変化 の 割合 で 力 を 数量的 に定 義できるはずである。　　すなわち　力 の 成分 は

　　　　　　　Fx = d /.dt [ m₀ u_x /√( 1 - u² / c² ) ] 、　Fy = d / dt [ m₀u_y /√( 1 - u² / c² ) ]

　　　　　　　Fz = d / dt [ m₀ u_z /√( 1 - u² / c² ) ]　　　　　　　　　　　　　 ( 25 )

　　　　このときの パワー　P 　は、　　Fx 　、　Fy 　、　Fz 　が 単位時間 にする 仕 事 の 量 であるから

　　　　　　　P = F_x u_x + F_y u_y + F_z u_z = d / dt [ m₀ c² /√( 1 - u² / c² ) ]　　　　　　　　( 26 )

　　　　この パワー は また 質 点 の エネルギー　の 増加する割合 であるから　( 26 )　を 積 分 して

　　　　　　　　　　　W = m₀ c² / √( 1 - u² / c² )　+ 　K　　　　　　　　　　　　　　 ( 27 )

　　　上式で、K = 0　とすると　W = m₀ c² / √( 1 - u² / c² )　=　m c² =　 E 　　m = m₀ / √( 1 - u² / c² )

　　　　　　　　　目 的 の 、　　 　　E = m c²　　　　にたどり　着　け　ました

　　　　　　　　　　　　　　　　　　こ の　ページ　の　Top　へ

◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆ ◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆ ◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆

　後 書 き　今回、難しい問題に挑戦むしましたが 相対性理論 に関する 全貌 がおぼろげに 理 解 できました

　　　　　　　　　　　　　　　ま と め

　　　　　 AA　　マイケルソン ・ モーレー の 実 験

　　　　　　　　　19 世紀 まで、光 は エーテル という 物 質 を 媒 体 して 伝 搬 すると考えられていた。

　　　　　　　　　1887年　この 実験結果　エーテル の 存 在 が 否 定 された。

　　　　　　　　　この成果は、第二次科学革命 の 端 緒　と評されている。　マイケルソン は ノーへ゛ル賞　受賞

　　　　　　　　　アインシュタイン の 相対性理論　構 築 までの 起 点とも 言えましょうか。


　　　　　BB　　ローレンツ 変 換

　　　　　　　　　ローレンツ は マイケルソン の 実験結果 を説 明 するために ガリレー 変 換 を変更して、

　　　　　　　　　局所時 (Local Time)　、　ローレンツ 収 縮　√(1 - u² / c²)　という　大胆な提唱 をした。

　　　　　　　　　私には、この ローレンツ変換 は アインシュタイン の 相対性理論 の 生みの親 のようにおもえました。


　　　　　CC　　相対速度 と 合成速度

　　　　　　　　　　　相対速度　= 　Va + Vb

　　　　　　　　　　　合成速度　=　 (Va + Vb) / ( 1 + Va ・ Vb / c² )


　　　　　DD　　物 体 の 質 量 ・ 長 さ と 移動速度　

　　　　　　　　　　　物 体の 質 量　と　移動速度　　　M 　=　 M₀/ √( 1 - v² / c² )

　　　　　　　　　　　物 体 の 長 さ 　と 移動速度　　　L　 = 　L₀ √( 1 - v² / c² )

　
　　　　　EE　　E 　=　 m c²　　の　式 の 誘 導

　　　　　　　　　　　言葉で表現すると 、2個の同一な完全弾性球を正面衝突させたときの物理現象を考察して 説 明。

　　　　　　　　　　　質量保存の法則 および 運動量保存 の法則の式に速度合成の式を用いて、質量の移動速度よる

　　　　　　　　　　　質量変化 の 式 を 導 く　　　　M 　=　 M₀/ √( 1 - v² / c^{2 )}

　　　　　　　　　　　さらに、運動量の各成分　p_x . p_y . p_z より 運動量 の 時間的変化の割合 で 力 を数量的に定義する。

　　　　　　　　　　　　　　　　　　　　　　　　　　　Fx 、 　Fy 、 　Fz 　

　　　　　　　　　　　パワー　P　は、　　Fx 、　 Fy 、　 Fz　 が 単位時間 にする 仕 事 であるから

　　　　　　　　　　　　　　　　P = Fx u_x + Fy u_y + Fz u_z = d / dt 〔 m₀ c² / (√( 1 - u² / c² ) 〕

　　　　　　　　　　　このパワーはまた質点のエネルギー　W　の増加する割合であるから、これを積分して

　　　　　　　　　　　　　　　　W = m₀ c² / √( 1 - u² / c² ) + K

　　　　　　　　　　　ここで 、　　　　K = 0 　　と し　　　　m = m₀ / √( 1 - u² / c² ) 　　だから

　　　　　　　　　　　　　　　　W = m c² = E　　　　　E =m c²　　　が　導かれる


　　　　　FF　　この 他 、光 は 重 力 によって 曲 げられる

　　　　　　　　　　アインシュタイン が 一般相対性理論 を 発 表 したのは　1915 年 。

　　　　　　　　　その直後 の 1919年 5月 29日 ちょうど 皆 既 日 食 がありました。

　　　　　　　　　　イギリス の 天文学者 　アーサー・エディントン は アフリカ の プリンシペ 島 に 遠 征

　　　　　　　　　　同 じく　 イギリス の 天文学者　アントリュー ・ クロンメリン は ブラジル へ 遠 。

　　　　　　　　　　2 観測隊 は 別々 の 地 に 向かったのは 天 候 により 観 測 ができなくなることを 配 慮 しての

　　　　　　　　　　周 到 な 準 備 だったと いう。

　　　　　　　　　　一般相対性理論 か正しければ、太 陽 の 向こう側 にある 星 から来る 光 は、太陽の

　　　　　　　　　　重力 によってゆがめられ、実際の位置 とは違う 位置 に、星が 見えるはずである。

　　　　　　　　　　観測結果 は 一般相対性理論 の 計算値 に近い 観 測 値 が得られた とのこと 。

　　　　世界中が 大 騒 ぎ となったそうです。　観測結果の成功の報 を受けたアインシュタインは特に驚かなかったという。

　　　　　　　　　　　　　　　　　　当 然 だと 、言 いた かった のでしょうか　　　　　　　　　　　　　


　　　　　　　　　　　　　　　　　　

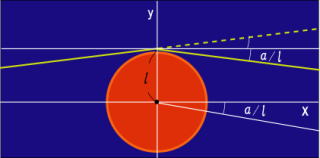
　　　　　　宇宙の彼方から 太陽 の縁を目がけて飛んで来た光 は、太陽 の重力 によって曲げられる。

　　　　　　一般相対性理論 の 理論上 の　計算値　は　1.75 秒　　(角度の単位 度 、分 、 秒 = 1 / 3600　度)

　　　　　　　　　　　　　　　　　　　　　　　　　 　　観測結果 は　1.61 秒　　であった　　　　　　　　

　　　　　　　ちなみに、ニュートン力学　での　理論値　は　0.875 秒　　で　一般相対性理論　の方 が 正しいことがわかった

　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

　　　　　　　　　　　　　　
　　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
　　　　　　GG　　　G P S 　( Global Positioning System )　　全地球測位システム

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　( こちらを参照ください )

　　　　　　　　　　　　　　 　　　　　　　　　　


　　　　　　　　　　　　　　　　　　　　　　　　　　　

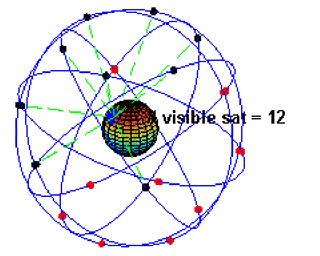
　　　　　　　　GPS は アメリカ合衆国 が 軍事用 に打ち上げた 約 30個 の GPS 上空にある 数個の衛星 からの

　　　　　　　　　　信号 を GPS で受け取り、受信者 が 自身 の 現在位置 を 知る システム である。　　

　　　　　GPS の 原理　GPS 衛星からの電波を受信し、発信・受信の時刻差に電波の伝搬速度 (光の速度と同じ30万km/s)

　を掛けることによって、その衛星からの距離がわかる。 3 個の GPS衛星からの距離がわかれば空間上の一点がきまる。

　　　　　　　　三 脚 の 原 理　　カメラ が 受信者の現在位置、三脚のそれぞれの 足の先端 がGPS　衛星の位置

　　ここで、GPS　をとりあげた 理 由 は 、この　GPS　システム　においても　一般相対性理論 が 活 躍 しております。

　　　　　　　　　　　　　　　　　すなわち、　　　　　　　原 子 時 計 の 遅 れ]

　　受信機側 での 信号処理 には、さまざまな 要 因 によるものが含まれるが、高速 で 運動する GPS 衛星 の 運動による

　　　　発振信号 の 時間 の 遅れ と、地 球 の 重力場 による 時間 の 遅れ である。

　　　　後者は、衛星軌道 の 擾乱 や 信号到達距離 の 湾 曲 、発振信号 の 時間 の 遅れ などを引き起こす。

　　　地上 の 時 計 は 、GPS 衛星 の 時計 よりわずかに 遅れる ので、GPS 衛星 の 時計 は、 これを 補 正 するため 遅 く

　　　　進むよう に 設 計 ^[1] されている。

　この 時間 の 遅 れ は相対論効果 を 考 慮 した 計算結果 と 高 い精 度 で 一致 しており、身近 な 相対性理論効果 の

　　　　　　　　　実 証 の 一つ として 挙 げ られる^[2]。 　

　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー


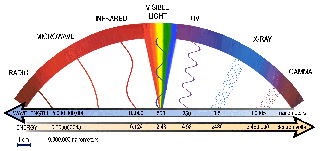
　　　　　　【 蛇　足 】 　　　　　　電 波 と 光 について


　　　　　　　　　　　　　　　 　電 波 と 光 の 性 質

　　　　　　 　　 　◆　　速 度 が 等しい　　30 万 km/s

　 　　　 　　　 ◆　　ともに、　波　である　　　振 動 数　　波 長 　で 表す

　 　　　　 　 　◆　　電 波 は 目 で 見えないが、　光 は 可 視 光 帯 　がある

　　　 　　　 　　　　　　　　　　

　　 　　　　　 ◆　　ともに、重 さ　がない　という

　　　　　　　　
　　　　ところが、　Yahoo　検 索 で 探したら 、 次 の ような 記 事 がありました　→　　光 の 重さ と 長　

　　一個 の 光 は　超 ひも　いい、 輻射エネルギー量 の 式より　 E = h ・ V 　(プランク乗数 × 光の振動数)　より　計算して

　　　　　　　　　　　　　　光　一個 の　重 さ　は　　　　　10- 44 g　

　　　　　　　　　　　　　　光　一個 の　長 さ　は　　　　　10- 33 cm　　　　　　と い う

　　　　　　　　　　　　　　　　　　　　　　摩 訶 不 思 議

　　　　　　　　　　★　　アインシュタイン　の　ノーベル 賞　　受 賞 理 由　は　【　光 量 子 仮 説　】　であった

　　　　　　　アインシュタインがノーベル賞をもらった理由とは？

アルベルト・アインシュタイン（アルバート・アインシュタイン、とも）は、ユダヤ人の有名な理論物理学者です。

彼は生涯でいくつか功績を残しましたが、そのうちの１つが、有名な　「相対性理論（相対論）」　と言うものです
。
１９０５年に「特殊相対性理論」を、そして１９１５年に「一般相対性理論」を発表しました。

また、彼は１９２１年、ノーベル物理学賞を受賞しています。

アインシュタインの残した功績で一番有名なものが「相対論」であり、ノーベル賞を受賞したのが相対論発表直後であるため、

アインシュタインが受賞したのは、相対論とは全く関係の無い、　「光量子仮説」　と言う物です。

光量子仮説とは、（後で詳しく説明しますが）一言で言うと　「 光 とは 粒 と 波 の 性質を持った物である 」　と言う説です。

光量子仮説が出てくるまで、「光は波である」と考えられていましたが、アインシュタインがこの考えを打ち破ったのです。

で、アインシュタインは光量子仮説によってノーベル物理学賞を受賞したのですが、

この話には、（真偽は定かではありませんが）ちょっとした　裏 話　があります。

相対性理論は、当時の物理学の常識を大きく覆した理論でした。

そのため、ノーベル賞選考委員は、本当は「相対性理論の発見」でノーベル物理学賞を彼に与えたかったのですが…

実は、当時の科学技術では、相対論が本当に正しいのかどうか、検証する事ができなかったのです。

また、その内容が非常に難解で、ノーベル賞選考委員たちに理解することもできませんでした。

権威あるノーベル賞を、そんな曖昧な物に与えるわけには行きません。

しかし、どうしてもノーベル賞を与えたい選考委員たちは、アインシュタインの他の功績をムリヤリ探し始めました。

そして発見したのが、特殊相対論と同年に発表された、光量子仮説。

「こりゃ良いや」とばかりに、ノーベル賞選考委員たちはこれに飛びつき、見事アインシュタインにノーベル物理学賞を与える事ができたのです。

ちなみに、相対論が本当に正しいかどうかは現在も検証が続けられています。

ただ、今（２００６年）のところ、相対論を否定する材料は、何一つ出てきておりませんので、ご安心を。

　　　　　　　　　　 　　　　　　こ の　ページ　の　Top　へ


　ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー


　　　　●　　　　【　質　量　１ グラム　の　エネルギー　】　　　　　2015.12.16　　追　記

　　　　　







　　◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆