FLT ; Fermat's Last Theorem
天才 数学者 たちが 挑 ん だ 最 大 の 難 問
【 x n + y n = z n 】
n が 2 より大きいとき、自然数解 を持たない
直角三角形 ピタゴラスの 定 理 はなじみあるが、
一見やさしそうに 見える上の式が世界中の数学者たちを 350年以上 も
肯定も否定もできずに悩ませてきたとは.
この F L T は数学界では 解けない問題の 代名詞 ともなっていたようです.
ところが 数年前、1993年 米国プリンストン大学教授の アンドリュ−.ワイルズ
がその解明に 成功し世界中の数学界に一大センセイションを巻 起こしたとのこと.
20世紀 数学の最大の収穫の一つとして 賞 賛 されました.
しかし 文献をみていると ワイルズ が フィニッシュを飾ったのはリレ−でのアンカ−
のように思えました.と言うのは長年にわたっての世界中の数学者がこの 解 明に一歩々積み
上げた 業 績 の上で 成し遂げられたように記されています.
日本人 数学者 では 谷山 豊、志村 五郎 が高く 評 価 されております
【追 記 】 Yahoo Q & A 記 事 を 参 照 して
Q ; フェルマ−の 最 終 定 理 について教えてください
A ; ベストアンサ−
フエルマ−の 最 終 定 理 が 誤 り であると 仮 定 すると、2 より大きな
ある 自 然 数 n について、方程式 xn + yn = zn には少なくとも
一組の 整 数 解 ( x. y. z )〓 ( a. b. c ) で、 a. b. c がいずれも
0 ではなく、 しかも二つずつ互いに 素 であるものが 存 在 する。
そのような解から、ある【 特 殊な 】性 質をもつ 楕 円 曲 線 を作ることができる。
それは フライ の 楕 円 曲 線 と呼ばれている
y2 = x (x - an)(x + bn)
このような 楕円曲線を 考えた フライ は、1983年 に次の 予想を 発 表した
【 フライの 楕円曲線 は モジュラ− ではない 】
この 予想を リベット が 1986年 に 証 明 した
この、フライの 楕 円 曲 線 が 存 在 しないことがいえれば
フェルマ−の 最 終 定 理 は正しい。
したがって フェルマ−の 最 終 定 理 を 証 明 するためには
【 すべての 楕円曲線 は モジュラ−である 】
ことを示せば十分である。
この 命 題 は 志村 〓 谷山 予想 と呼ばれている
厳 密には、フェルマ−の 最終定理 を 証明するためにはこの予想の一部を
証 明 するだけでよい
ワイルズ は 1995年 に発表した論文にいて、【 半 安 定( semi-stable )】
と呼ばれる性質をもつ 楕円曲線 について 志村 〓 谷山 予想 を 証 明 した。
一方、フライの 楕円曲線 は 半安定 である。
よってワイルズの結果から フライの 楕円曲線 は存在しないことが導かれる。
こうして フェルマ−の 最 終 定 理 は 完 全に 証 明された。
★★★★★☆☆☆☆☆●●●●●●▼▼▼▼▼▽▽▽▽▽◆◆◆◆◆◇◇◇◇◇★★★★★
この 記 事 を見た 感 想
日本人 数 学 者 谷山 志村 両 氏が 8合目か 9合目まで きていたのに
最 後 は とんび、鳶(ワイルズ)に 油らげ をさらわれたような 気がして
残 念 でした
.
また、文 献 には 数 学 的 解 明 内 容 は 聞いたこともない 数 学 専 門 用 語
( 理想数、複素平面 双曲型空間、モジュラ- 等 )で 説明されているので
遠くの山でも見ているようにしか 理 解できないが、
なぜかとてつもなく むづかしい 問 題 のように感じとれました.
★ √2 の 不思議. 無理数 の 発見
両辺が 1 の直角二等辺三角形の斜辺の長さは、 ピタゴラスの定理によって √2 である.
しかしご存じのように √2 〓 1.41421356237309504880で、
これは 有 理 数 ではない.
√2 ( 無 理 数 ) の発見 はギリシャ人にとって大きな驚きであった.幾何学的には、
はっきりした「長さ」として描けるのに、彼らの数の概念では表せない数が存在したのだ.
この驚きがきっかけとなって、従来の素朴な「 数原子論 」が破綻し、自然は「人間の考えどうりには
できていない」という認識が生まれたのである.
数学者は、また哲学者であることが多いようです.哲学的思考をさまよいながら数学上の
思索をしているのでしょうか. 無理数 の発見以前、0 の発見 にもかり時間がかかったようです
“ 0 匹の魚 を買いに行く人はいない ” と言う 昔 話
有 理 数 無 理 数
整数 m, n (≠0)によって m/n と表 小数で表したとき、有限小数にも
わせるような数を有理数という. 循環小数にもならない実数.
小数展開すれば、有限小数か循環小数なる.
(例) 1/20 〓 0.05 (例) √2 〓 1.41421356---------
1/7 〓
0.142857142857---
π 〓 3.141653589---
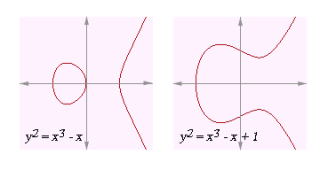
楕円曲線 は 具体的 にどんな形のものか、イメ−ジできない
フ ラ イ の 楕 円 曲 線 方程式
y2 〓 x ( x - an ) ( x + bn ) 〓 x 〔 x2 - ( an - bn ) x - an.bn 〕
〓 x3 - ( an - bn ) x2 - an.bn x
簡単な 方程式 の 場合の 曲 線 を上 図に示します