newp - 1

　　ピタゴラス の 定 理

　ピタゴラスの定理とその証明　　Yahoo　検索より　　ウィキペディア　ピタゴラス の 定 理

　　　　　　　直 角 三 角 形　(　三平方 の 定理　)　　　a² ＋ b²=　 c²　


　　　　　ピタゴラス の 定 理 は 三角関数 の 公式 の 中にも 同 等 のものがあることに 気づき ました

　　　　　　　　　　　　　　　sin²θ ＋ cos²θ 　= 　1　

　　　　　　直 角 三 角 形 の 辺 の 長さ　a b c 　c 　は　斜 辺 とすると

　　　　　　　　　　sin θ= a / c 　　cos θ = b / c　　sin ² θ = a² / c² cos ² θ = b² / c²

　　　　　　　　　　　　　sin² θ + cos² θ = a² / c² + b² / c² = ( a² + b² ) / c² = 1

　　　　　　　　従って　　a² + b²　= c² 　　　ピタゴラス　の　定 理　　が 導 か れ る


　　　　　　　　　　　　これに　気づいた　時　　　ひとり　にがわらい


　　　　　　　　その後、調べたら　ウィキペディア　ピタゴラス の 定 理　に　

　　　　　　　　　オイラー の 公 式 を 使った　詳 し い　ものがありました　


　　　　　　　　　がっかり　　　でも　これに　気づ い た こと で 満 足 するか


　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★


　ピタゴラス の 定 理 　の 証 明 法 法　は　100 通 り 以 上　あると いわれます。

　　　　　　　　　　　代 表 的 な　証 明 例 を　拾って　みました


　　　●　　　　　証 明 て゜使 う　図 形 を 先 に 掲 げて おきます


　　　　　　　　　　　　　　　　

　　　　　　　　　　　　証 明 ー 1 　　　　　　　　　　　証 明 ー 2.1　　　　　　　　　　　証 明 ー 2.2



　　　　　　　　　　　　　　　　

　　　　　　　　　　 　証 明 ー 3　　　　　　　　　　　証 明 ー 4　　　　　　　　　　　　証 明 ー5



　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　証 明 ー6゜　　　　　　　　　証 明 ー 7.1　　　　　　　　　　　　証 明 ー 7.2




　　　　　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★




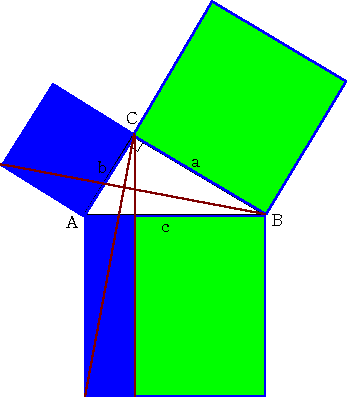
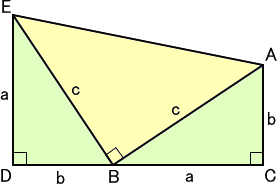
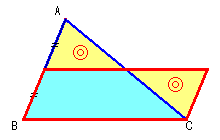
　　　　　　◆　　　証 明 ー 1　　　上 図　－　1　　参 照

　　　　　　　　　等 積 変 形 と 三角形 の 合 同 により、図 の 同 じ 色 の 部 分 の 面 積 は 等しい

　　　　　　　　　　　　　　この 証 明 方 法 は、ユークリッド によるものと 言われております

　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　補 足 説 明　

　　　　　　　　　　　　　　　　　私 は 、代 数 的 に　捉えて　みました
　　　
　　　　　　　　　証明ー1　図　において　青 色 の 正方形　と 　長方形 の 面 積　が等しく、

　　　　　　　　　　　　　　　　　　　緑 色 の 正方形 　と 　長方形 の 面 積　が等しい ことを　示 し て 、　　

　　　　　　　　　　　　　　a² +　b² 　=　 c² 　　が　得られれば　よい

　　　　　　　　　青 色 の 正方形　一辺 の 長さ　b　　長方形 　タテ の 長さ　c　ヨコ の 長さ x とする

　　　　　　　　　青 色 の 正方形　の 面 積　=　 b²　 　　　　　長方形　の 面 積　= 　c x
　
　　　　　　　　　青 色 の 正方形　の 面 積　　と　長方形　の 面 積　が 等しい とすると

　　　　　　　　　　　　　　　　　　b² 　= 　c x　　　　　x 　= 　b² / c

　　　　　　　　　緑 色 の 正方形　一辺 の 長さ　a　　長方形 　タテ の 長さ　c　ヨコ の 長さ ( c - x )

　　　　　　　　　緑 色 の 正方形 の 面 積　= 　a²　　長方形 の 面 積　= 　c ( c - x )

　　　　　　　　　　　　　　　　　　a² 　= 　c ( c - x )

　　　　　　　　　　　　x 　= 　b² / c　　を代入すると　　a² 　= 　c ( c - b² / c) = c² - b²

　　　　　　　　　　従 っ て　　　a²　+　b²　=　c²　　　が 得られた　　　　証 明 　終わり


　　　　　　追　記　　等 積 変 形 と 三角形 の 合 同 により、図 の 同 じ 色 の 部 分 の 面 積 は 等しい　

　　　　　　　　　証 明　－1　　において　　二つの　三角形　が　合 同 であることは 理 解 できる

　　　　　　　ところが　青色 の 正方形 の 面 積 と 長方形 の 面 積 がそれぞれ 三角形 の 面 積 に 等しい　

　　　　　　　　　　　　　という　等積変形 は 自力 では 理 解 できなかった

　　　　　　　　　　　　　調べたら 分かりやすい 図 解 がありました

　　　　　　　　　　　　 　　　　　　　
　
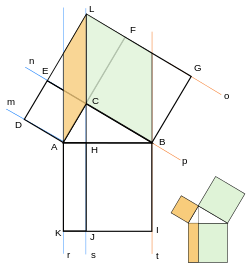
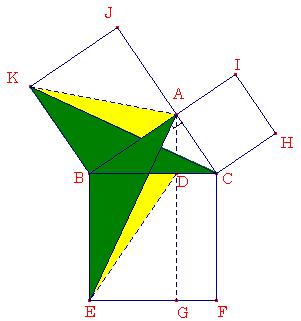
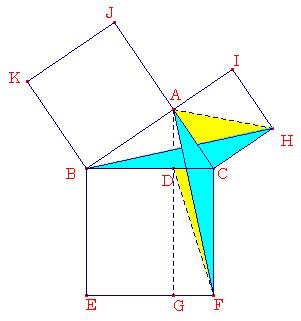
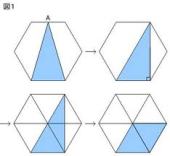
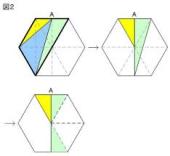
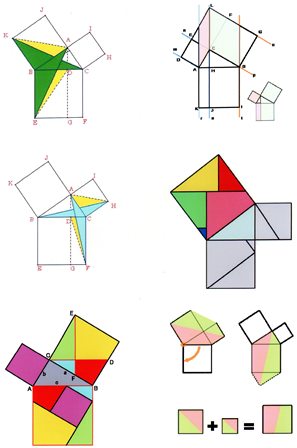
　　　　　　　　　　　　fig 1 　　　　　　　　　　fig 2 　　　　　　　　　　　fig 3 　　　　　　　　　　　　fig 4


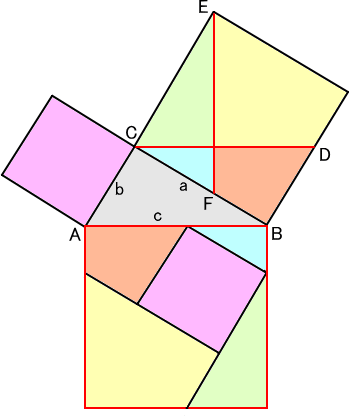
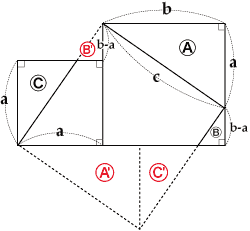
　　　　　　　　　◆　　　　fig - 2 　が 理 解 　し易かった


　　　　　　　　　　　　先ず、正方形　b ²　を　等積変形 して　橙 色　の　平行四辺形　を作る　

　　　　　　　　　　　　ここで　三角形　ABC LCF　は 合 同　　従って　AB = LC = c

　　　　　　　　　　　　次に　平行四辺形 を 等積変形 して　　　　長方形 を 作る

　　　　　　　　　　　　更に、　これを　下に　ずらせば　fig - 1　の　青色　長方形　が　得られる
　　　　　　　　

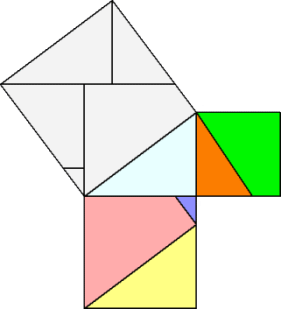
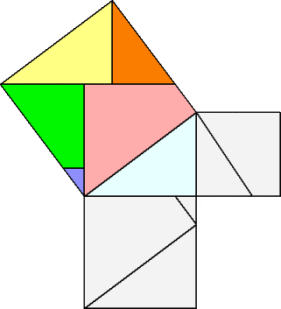
　　　　　　　　　◆　　　　fig - 3　　と　　fig - 4　　は　正方形 を　三角形 に　等積変形　する

　　　　　　　　　　　　　　　fig - 1　の　三角形　に　等しい

　　　　　　　　　　　　　　　 ようやく 、　fig - 1　が　理 解　できました


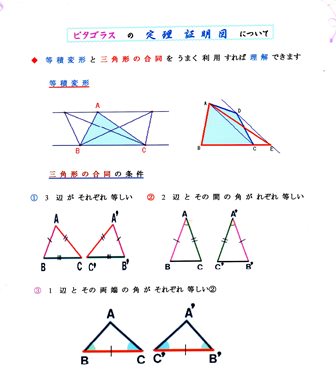
　　　　　　　　　◆　　　参 考 資 料　　等積変形 と　三角形 の 合 同　

　　　　　　　　　　 　　　　

　　　　　　　　　　　　　　　　　　　　　



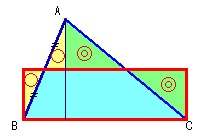
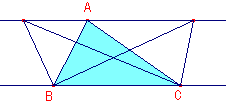
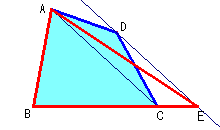
　　　　　　　　　　　　　　　　　三角形 の 合 同 の 条 件

　　　　　　　　　　　


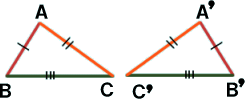
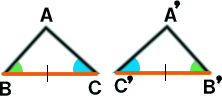
　　　　　　　　　　　　　 ①　　　3　辺 が それぞれ 等しい

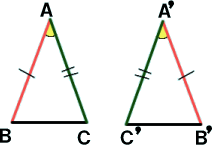
　　　　　　　　　　　　　②　　　2　辺 と その 間 の 角 が れぞれ 等しい

　　　　　　　　　　　　　③　　　1　辺 と その 両 端 の 角 が それぞれ 等しい



　　　　　　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★



　　　　　　◆　　　証 明 ー 2　　　 作 者　不 明

　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　2.1　図　　　　　　　　　　　　　　　2.2　図　　　　　　　　　　　　　　3.1　図　　　　　　　　　　　3.2　図

　　　　　　　　　2.1　図　において　外接正方形 の 面 積 は　( a + b ) ²

　　　　　　　　　　　　　　　　　　　内接正方形 の 面 積 は　　　c ²

　　　　　　　　　　　内接正方形 の 面 積　c ²　　は　外接正方形 の 面 積　( a + b ) ²　より

　　　　　　　　　　　4　個　の　直角　三角形　の 面 積　を 引 け ば 得られる

　　　　　　　　　　c ² = 　( a + b ) ²　- 4 (a × b / 2) = a ² + 2 a b + b ² - 2 a b

　　　　　　　　　　　　　　　c ² = a ² + b ² 　　が　成 立　する

　　　　　　　　　　また　　2.2　図　も　　同 様　　です

　　　　　　　　　　　　　　この　証 明　図　は　一番　理 解 しやすい　　


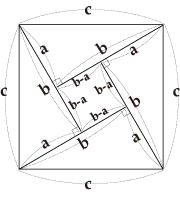
　　　　　　　　　　　尚 、　3.1　図　　3.2　図　は　江 戸 時 代 の 和 算 に　あったようです

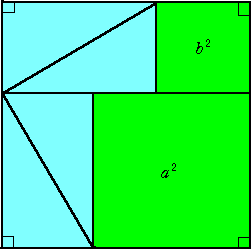
　　　　　　　　　　　　　　　3.1　図　は　一辺　が　c　の　正方形 の 面積 は

　　　　　　　　　　　　中 の　4 個 の 直角三角形　と　小 さい　正方形 の　面 積 を 足 せ ばよい

　　　　　　　　　　　　　　　
　　　　　　　　　　　　c ² = 4 (a .b / 2) + (b - a) ² = 2 . a b + b ² - 2 . a .b + a ²　= b ² + a ²

　　　　　　　　　　　　　　　　　　　　c ² = a ² + b ²　　　が 得 られる


　　　　　　　　　　さらに 、　 3.2　図　について　

　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　図　が　小さくて　交点　が　見にくいので　言葉で　説明します

　　　　　　　　　b　の　中にある三角形を　c　の正方形に　移します

　　　　　　　　　a　の　中にある三角形を　c　の正方形に　移します

　　　　　　　　　次に　b　の正方形　の中にあるちいさい　三角形　＠　を　c　に移します

　　　　　　　　　a　の　正方形と　b 　の　正方形　が　c　の　正方形に　移りました

　　　　　　　　　　　　　従って　　a ² + b ² = c ²　　　となります


　　　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★



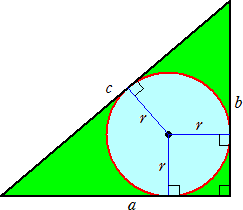
　　　　　　◆　　　証 明 ー 3　　　内 接 円 の 半 径 を 巧 妙 に 利 用 する 証 明

　　　　　　　　　　　　　　　　　　

　　　　　　　　上 図 に 記 号 を 追加　します　三角 の 頂 点 を　A B C　　円 の 中 心 を　0　とする

　　　　　　　　底 辺　AB = a 　高 さ　BC = b　　斜 辺　BC = c　

　　　　　　　　各 頂 点 から 中心　0 に 直 線 を 引 く　　すると　3 個 の 三角形 A0B B0C C0A ができる

　　　　　　　　ミドリ　色 の 三角形 の 面 積 は　a b / 2 　ABC = a r / 2 　B0C = b r / 2 　C0A = c r / 2

　　　　　　　　従って　a b / 2 = a r / 2 + b r / 2 + c r / 2 = (a + b + c) r / 2

　　　　　　　　　　　　　a b = (a + b + c) r

　　　　　　　　接 線 の 長さ はそれぞれ等しいので　c = (a - r) + (b - r) = a + b - 2 r 　　r = (a + b -c) / 2

　　　　　　　　　　　　 (a + b + c) (a + b - c) = 2 a b　　　a ² + b ² = c ² 　が 得られる

　　　　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★



　　　　　　◆　　　証 明 ー 4　　　上 図　－　4　　参 照


　　　　　　　　 　合 同 な 図 形 を 巧 妙 に 利 用 する 証 明

　　　　　　　( この 証明方法 は レオナルド. ダビンチ によるものと 言われております )


　　　　　　　　　　　レオナルド・ダ・ヴィンチ は

　　　　　　　1452年4月15日 - 1519年5月2日　は、イタリアのルネサンス期　を代表する　芸術家。

　　　　　　　絵画、彫刻、建築、音楽、科学、数学、工学、発明、解剖学、地学、地誌学、植物学など

　　　　　　　様々な分野に　顕 著 な 業 績　　を 残 し、「万能人 」 と　異名 などで親しまれている。

　　　　　　　　　　　　　　　　　　　　　



　　　　　　　　　　　　　　　　　　　　　　　

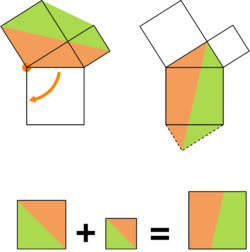
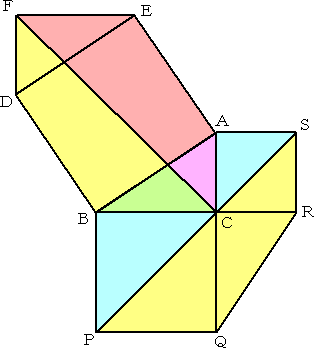
　　　　　　　　　　　　　　　　　　fig - 5 　　　　　　　　　　　　　　　　　　fig - 6

　　　　　fig - 5 において、四角形 ＥＦＣＡ、ＦＤＢＣ、　ＡＢＰＳ、ＰＱＲＳ の 面 積 は全て等しい。

　　　　　このことから、五角形 ＦＤＢＡＥ と 凹七角形 ＡＣＢＰＱＲＳ の 面 積 は 等しい。

　　　　　ここで、△ＥＦＤ と △ＱＣＲ の 面 積 は 等しいことに 注意。

　　　　　よって、正方形 ＤＢＡＥ の 面 積 は、　２つ の 正方形　ＢＰＱＣ　ＡＣＲＳ　の　面積の和

　　　　　　　に等しい。　とありましたが　理 解 できませんでした。

　　　　　fig -6　を　見つけたので　納 得　しました　　7角形 を 90度 回転 した 図 がわかりやすい


　　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★



　　　　　　◆　　　証 明 ー 5　　　上 図　－　5　　参 照

　　　　　　　　　　　　台 形 の 面 積 を 利 用 す る証 明

　　　　　【 この 証 明 は、ガモフィールド ( 米 第20代 大統領 ) によるものと言われている】

　　　　　　　　　　　　　→　妻　　


　　　　　　　この 台形 を 逆 にして 上 に 積 み重 ねる と 一辺 が　(a + b) の 正方形 が できます

　　　　　　　この 正方形 は 直角三角形 a b c 　4 個 と 一 辺 が c 　の 正方形 と　なっております

　　　　　　　　　(a + b) ² = 4 (a b / 2) + c ² = 2 a b + c ² = a ² + 2 a b + b ²

　　　　　　　　　　　　従って　　　c ² 　= 　a ² + b ² 　　　が 得られ ます

　　　　　　　　　　　　　　　 理 解 しやすい 　証 明 図 　です


　　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★



　　　　　　◆　　　証 明 ー 6　　　上 図　－　6　　参 照


　　　　　　　　　　　　　図 形 の 組 み 換 え による 証 明

　　　　　　　　　　( この 証 明 方 法 は 、パスカラ (インドの数学者) によるものと 言われて おります)

　　　　　　　　　　　　　　　　　　　　　　　　　　　

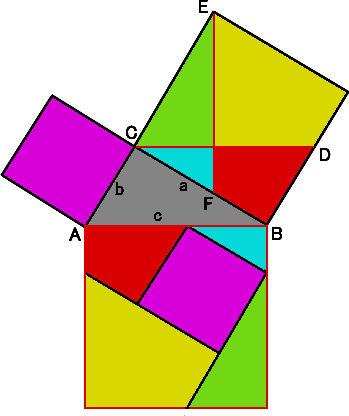
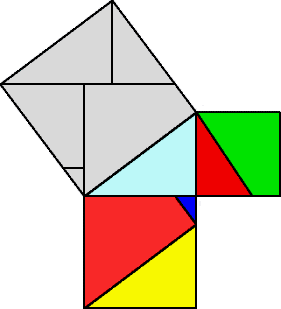
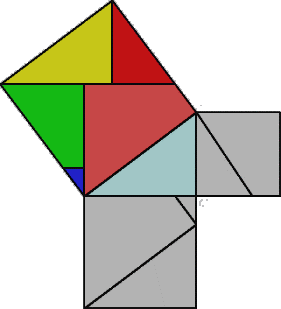
　　　　　　　　　　　　　 fig 6.1 　　　　　　fig 6.2 　　　　　　　　　　　 　 fig 6.3 　　　　　　　　 fig 6.4


　　　、　　　　　fig 6.1　 fig 6.2　 　この　説 明 図 は 眺 めて いるだけで 理 解 できる

　　　　　　　　直角三角形　A B C 　の 斜 辺　A B　に 平 行 な 直 線 を　 C 点 より 引 き

　　　　　　　　　　　　　　a　正方形 と 交 わる 点 を　 D とする　　　　fig 6.2

　　　　　　　　さらに　a　正方形　の 頂点　E より　平行線 に 直行する タテ 線 を 引くのが　 ミ ソ　fig 6.1

　　　　　　　　　a　正方形　は　2 個 の 直角三角形　と　2 個 の 四角形 に 分けられる

　　　　　　　　この　2 個 の 直角三角形 は 　A B C　と 合 同 である　従って、　C F = C D = b

　　　　　　　　図 形 の 面 積 は 　タテ ヨコ に ずらしたり 　裏 返 したり しても 変わらない。

　　　　　　　　a　正方形 の 4 個 の 図 形 は　c　正方形 　の 4 隅 に 移 動 　きる

　　　　　　　　すると　中に　四角い　空き地 ( 一 辺 が　b 　の正方形 )　が 残 る　

　　　　　　　　　この　空　き　地　に　b　正方形　を　スッボリ　はめ込む　ことができる

　　　　　　　　　　　　　c ² = a ² + b ²　　が　証 明 できた

　　　　　　　　　　　　　　fig 6.3 　も　ig 6.4　　同 様　で す


　　　　　　　　　　　　他 、　ピタゴラス の 定 理 　 アニメ 4　 による 証 明　　　　Youtube　より


　　　　　　　　　　　


　　　　　　　　　　　

　　　　　　 こ の 　ページ　 の 　Top　　へ　　　　http--kame3.org-ver6-newpage1.htm


　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★