Internet Surfing で Youtube を 楽 しん で おります
目 次
★ 積 分 で 面 積 を 求 め る
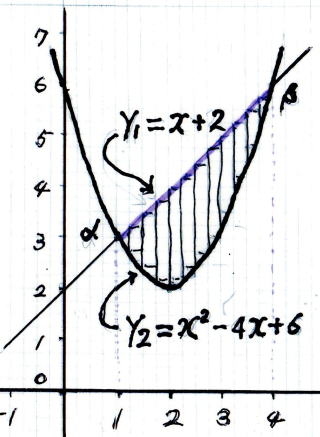
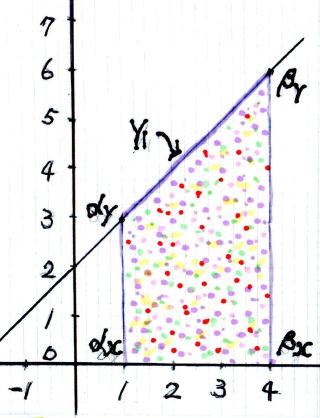
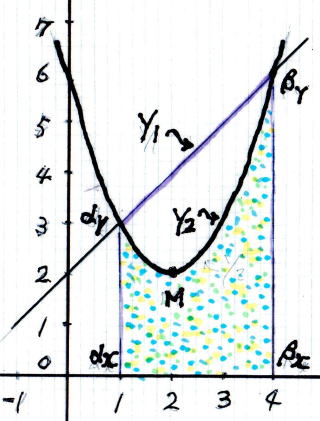
★ x α の 不 定 積 分 の や り 方 【 高校数学 Ⅲ 】 動 画 Youtube
微 分 ⇔ 積 分 x α の 微 分 → (1 / α) x ( α-1 )
x α の 積 分 → ∫ x a d x = 【 1 / ( d + 1 ) 】 x ( d + 1 )
∫ f ( x ) d x = F ( x ) 積 分 は F ( x ) 微 分 したら f ( x ) となる F ( x ) を 探 す ことである
● 計 算 例
1) ∫ x 4 d x = ( 1/5 ) x 5 + C
2) ∫ x - 3 d x = ( - 1/2 ) x - 2 + C
3) ∫ 3 √x d x = ∫ x 1/3 d x = ( 1/ ( (1/3) + 1) ) x 1/3) +1 d x = ( 4/3 ) x 4/3 + C = (4/3) x 3 √3 + C
4) ∫ ( 1 / 4 √x 2) d x = ∫ x - 2/4 d x = 2 x 1/2 + C = 2 √x + C
● 定 数 倍 関 数 の 積 分
∫ k f (x) d x = k ∫ (x) d x
● 関 数 の 和 および 差 の 積 分
1) ∫ f 1 (x) dx + ∫ f 2 (x) d x = ∫ ( f 1 (x) dx + ∫ f 2 (x) ) d x
2) ∫ f 1 (x) dx - ∫ f 2 (x) d x = ∫ ( f 1 (x) dx - ∫ f 2 (x) ) d x
● 関 数 の 置 換 積 分
1) ∫ x ( 1 - x ) 5 d x 1 - x = t と お く x = 1 - t d x / d t = - 1 d x = - d t
∫ x ( 1 - x ) 5 d x = ∫ ( 1 - t ) ｛ 1 - ( 1- t ) ｝5 ( - d t ) ｝
= - ∫ ( 1 - t ) t 5 d x = ∫ - ( t 5 - t 6 ) d x = - ( 1/6) t 6 + ( 1/7 ) t 7 + C
= - ( 1/42 ) t 6 ( 7 - 6 t ) + C = - ( 1/42 ) ( 1 - x ) 6 ( 6 x + 1 ) + C
2 ) ∫ f ( x ) d x = ∫ f ( g (t) ) g ´(t) d t x = g ( t ) という 置 き 換 え
| f(x) | F(x) = ∫f(x)dx | 備考 |
|---|---|---|
| xa | xa+1/(a+1) | a は -1 以外の実数 |
| 1/x | log e |x| | log は 自然対数 |
| sin (x) | -cos (x) | |
| cos (x) | sin (x) | |
| sec2 (x) | tan (x) | |
| exp (x) | exp (x) | |
| 1/(√(1 - x2)) | arc sin (x) | |
| -1/(√(1 - x2)) | arc cos (x) |
★ 部 分 分 数 分 解
○分数×分数＝分数－分数？
＜先 生＞ 今日は、最初に「かず遊び」をちょっとしてみようか。
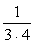なる分数の面白い性質として、
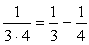
のように分解することができる。２つの分数の積が２つの分数の差と同じ値になるということだ。右辺を通分することで簡単に確認できるだろう。それでは同様に考えると、
①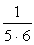 
② 
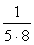
はどう分解できるだろうか。
＜まなぶ＞ はい、①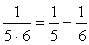 
，②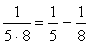 
でしょうか。
＜よしお＞ ②はおかしいよ。右辺を通分すると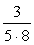 
だから左辺と一致しないだろう。
＜先 生＞ その通り。安易に差の形に分解できるわけではない。②の場合は、さらに分子の３を１に変えるために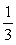 
を掛けておく必要がある。従って、
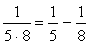となる。では、いったいどういうときに、単純に積の値が差の値と一致するのだろうか。
＜かず子＞ 右辺を通分したときに、分子の値が１になっていれば問題ないわけですから、
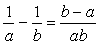
より左辺の分母にある２数の差が１のときだと思います。
＜先 生＞ そうだね。左辺の分母の２数の開きがキーになっている。①の場合は分母の２数の差をとると、
６－５＝１
だね。この値１が分子の値と一致していることが大事なんだ。これを
１＝６－５
と見てやる。そうすると、
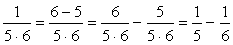
次に②の場合だが、分子の差は、
８－５＝３
左辺の分子の値１とは一致しない。だから３を１に変える必要が出てくる。
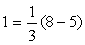
よって②は、
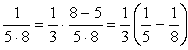
となるということだ。
結局、この分解のメカニズムは、分数の差の形に分解したあとに、左辺の分母の２数の差で右辺を割ってやればいいということだ。
まなぶ、自分で問題を考えて分解してごらん。
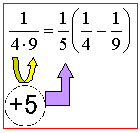＜まなぶ＞ はい、例えば、
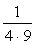は、分母の差が5だから、
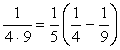
となります。
＜先 生＞ さて、それでは今日の本題だ。この変形を部分分数分解というが、このアイデアが数列の和の計算で実は応用できるんだ。
| ex) 次の数列{an}の初項から第n項までの和を求めよ。 (1) 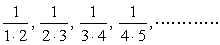 (2) 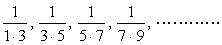 (3) 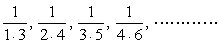 (4)  |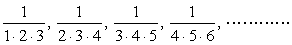
＜先 生＞ まず(1)からだ。どの項も部分分数分解されたがっているのが分かるだろうか。ひとつひとつやるのは大変だから、一般項で考えて分解してみよう。よしお、数列の一般項は何かな。
＜よしお＞ 分母の２数の積のうち、前の数の並びはn、後ろの数はn+1ですから、一般項は、
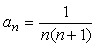
となります。
＜先 生＞
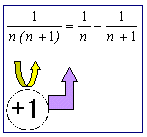ではこの一般項に対して部分分数分解をしてみようか、かず子。
＜かず子＞ はい、 (n+1)-n=1 ですから差は１、したがって、
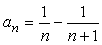
となります。
＜先 生＞ よって求める和は、
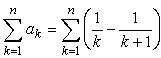
となるね。さて、あとはこの和を求めればいいのだけれど残念ながらベキ和の公式は使えない。そこで実際に書き抜くんだけど、さあここでちょっとノートの無駄遣いをすることになる。次のようにk=1，2，3，……，nを代入した項の値を縦に書いていこう。
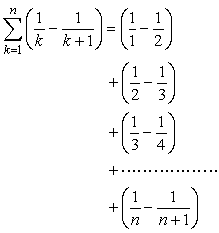
さあ、この計算をよくみてごらん。分解された項の中の数がその次に分解された項の数と相殺されて次々に消えていく。そうして最終的に残るのは、最初の項の1と最後の項の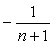 
だけだ。結局、
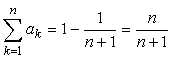
となるわけだ。
＜まなぶ＞ うわあ、なんかドミノ倒しみたいだな。
＜先 生＞ うん、いい表現だね。では次の(2)の問題にまなぶ命名のドミノ倒しを利用してみようか。まなぶどうなる。
＜まなぶ＞
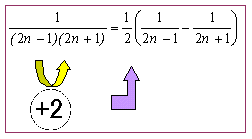えーと、まずは一般項からですよね。分母の積をみて前の数は、初項１公差２の等差数列より一般項は2n-1、後ろの数はそれより２多いんだから2n+1、だから一般項anは、
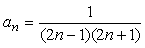
となります。次に、分母の２数の差は、(2n+1)-(2n+1)=2。よって２で割って、
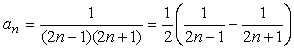
あとは和をドミノ倒しで求めるだけです。
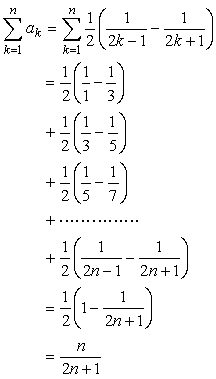
できました。
＜先 生＞ どうだろう。消え方も鮮やかだけど、和の値も随分美しくまとまるものだね。それでは(3)をよしおやってごらん。
＜よしお＞
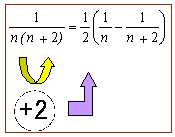まず一般項は、
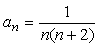
です。次に分母の２数の差は、(n+2)-n=2ですから式変形すると、
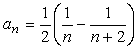
となります。よって、
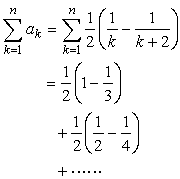
先生、上手く消えません。
＜先 生＞ そうだね。でも次の項は何だろう。
＜よしお＞ はい、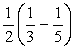
です。
＜先 生＞ そうすると、第１項目の部分分数分解された数のうち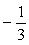 
と相殺されそうだね。もう少し頑張って、書きぬいてみよう。
＜よしお＞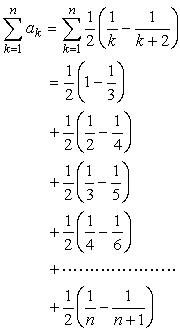 
となります。
＜先 生＞ どうだろう。少しは消え方が見えてきただろうか。実はこのドミノ倒し、倒れ方がちょっと凝っていて一つ置きになっているんだ。そこで、最後の方の項もk=n-2，n-1，n項ぐらいを書いてやらないと消え方がはっきりしない。 ＜よしお＞
★ 絶 対 値 ← Youtube 動 画
絶 対 値 Ⅰa Ⅰ Ⅰ- a Ⅰ は ゼ ロ からの 距 離 ゼ ロ からどれだけ 離れて いるか で
+ a で も - a で も 距 離 は a である
絶 対 値 を 含 む 方 程 式 不 等 式 習 っ た 記 憶 が ない
★ 因 数 分 解 基 本 編 高 校 数 - Ⅰ ← Youtube 動 画
基 本 編 は 中 学 で 習 っ た 公 式 を 使 う
( x + a ) ( x +b ) = x 2 + ( a + b ) + a b a 2 - b 2 = ( a + b ) ( a - b )
く く り 出 し
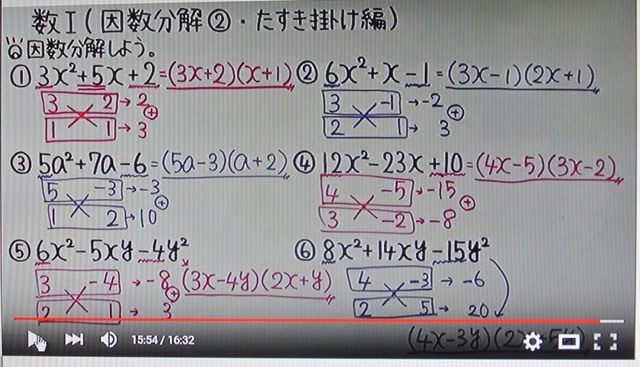
因 数 分 解 で たすき 掛 け の 裏 ワ ザ は 知 りません でした
応 用 編 は 文 字 を 含 む たすき 掛 け
★ 因 数 分 解 公 式
① ( x + y ) ( x - y ) = x 2 - y 2 青 字 は 証 明 展 開 式
x 2 + x y - x y - y 2 = x 2 - y 2
② ( x + y ) 2 = x 2 + 2 x y + y 2
x 2 + x y + x y + y 2 = x 2 + 2 x y + y 2
③ ( x - y ) 2 = x 2 - 2 x y + y 2
x 2 - x y - x y + y 2 = x 2 - 2 x y + y 2
④ ( x + y ) 3 = x 3 + 3 x 2 y + 3 x y 2 + y 3
⑤ ( x - y ) 3 = x 3 - 3 x 2 y + 3 x y 2 - y 3
⑥ x 3 + y 3 = ( x + y ) ( x 2 - x y + y 2 )
⑦ x 3 - y 3 = ( x - y ) ( x 2 + x y + y 2
⑧ ( x + y + z ) 2 = x 2 + y 2 + z 2 + 2 ( x y + x z + y z )
( A + z) 2 = A 2 + 2 A z + z 2 = ( x + y ) 2 + 2 ( x + y ) z + z 2
= x 2 + 2 x y + y 2 + 2 x z + 2 y z + z 2
= x 2 + y 2 + z 2 + 2 ( x y + x z + z z )
⑨ x 3 + y 3 + z 3 - 3 x y z = ( x + y + z ) ( x 2 + y 2 + z 2 - x y - x z - z x )
( x + y ) 3 - 3 x y ( x + y ) + z 3 - 3 x y z ( x + y ) 3 = x 3 + 3 x 2 y + 3 x y 2 + y 2
( x + y ) 3 + z 3 - 3 x y ( x + y ) - 3 x y z
A 3 + z 3 - 3 x y A - 3 x y z A = x + y
( A + z ) 3 - 3 A z ( A + z ) - 3 x y ( A + z )
( x + y + z ) 3 - 3 ( x + y ) z ( x + y + z ) - 3 x y ( x + y + z )
( x + y + z ) ｛ ( x + y + z ) 2 - 3 ( x + y ) z - 3 x y ｝
( x + y + z ) ( x 2 + y 2 + z 2 + 2 x y + 2 x z + 2 z x - 3 x y - 3 x z - 3 z x )
( x + y + z ) ( x 2 + y 2 + z 2 - x y - y z - z x ) E n d
● 私 の 展 開 式 力 づ く で やって おりました
x 3 + y 3 + z 3 - 3 x y z = ( x + y + z ) ( a1 + a2 + a3 + ・・・・ + an )
と 展 開 で き る こ と を 確 か め て み る
｛ x 3 + y 3 + z 3 - 3 x y z ｝ / ( x + y + z )
この式の割り算は、先ず x 3 + y 3 + z 3 - 3 x y z より x 2 ( x + y + z ) = x 3 + x 2 y + x 2 z を 引 き ます
さらに y 2 ( x + y + z ) を 引 き ま す
さらに z 2 ( x + y + z ) を 引 い て 完 了
◆ ｛ x 3 + y 3 + z 3 - 3 x y z ｝ - ( x 3 + y x 2 + z x 2 )
= y 3 + z 3 - 3 x y z - y x 2 - z x 2
◆ ( y 3 + z 3 - 3 x y z - y x 2 - z x 2 ) - ( x y 2 + y 3 + z y 2 )
= z 3 - 3 x y z - y x 2 - z x 2 - x y 2 - z y 2
◆ ( z 3 - 3 x y z - y x 2 - z x 2 - x y 2 - z y 2 ) - ( z 2 x + z 2 y + z 3 )
= - 3 x y z - y x 2 - z x 2 - x y 2- z y 2 - x z 2 - y z 2
= - 【 ( 3 x y z ) + x ( y 2 + z 2) + y ( x 2 + z 2 ) + z ( x 2 + y 2 )
① ② 式 に x y z ⇔ 1 2 3 を 代 入 し て 計 算 して み る
① 式 ｛ x 3 + y 3 + z 3 - 3 x y z ｝
= ( x + y + z ) ( x 2 + y 2 + z 2 - x y - x z - z y )
左辺 1 + 8 + 27 - 3 × 6 ＝ 18.
右辺 6 × ( 1 + 4 + 9－2－3－6 ) ＝ 18
② 式 ｛ x 3 + y 3 + z 3 - 3 x y z ｝
= ( x + y + z ) ( x 2 + y 2 + z 2 ) - 【 ( 3 x y z ) + x ( y 2 + z 2 ) + y ( x 2 + z 2 ) + z ( x 2 + y 2 ) 】
左辺 1 + 8 + 27 - 3 × 6 ＝ 18.
右辺 6 × ( 1 + 4 + 9 ) － 【 6 + 13 ＋ 20 + 15 】 ＝ 84 － 54 ＝ 30
左辺 ≠ 右辺
① 式 の よ う な スマート な 式 に な ら な か っ た
★ 因 数 分 解 １ 因 数 分 解 と は 展 開 の 逆 を すること
★ 因 数 分 解 公 式 集
★
★
★
★
