積分で面積 を求める
　　　　　　　　　　　　　　　　　　　三 輪 次 男

s - 35

★　　 1 次 関 数 の 直 線 と 2 次 関 数 の 曲 線 に 囲まれた 面 積 を求める

　　　　　　　　　　　　　1 次 関 数　　　　y₁ = x + 2

　　　　　　　　　　 　　2 次 関 数　　 　y₂ = x² - 4x + 6


　　●　　　数 十 年 前 に 習った 計 算 の 仕 方

　　　　　　　　　　　　　　

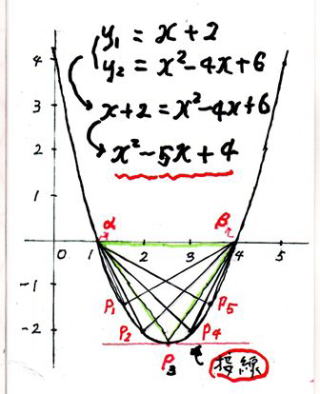
　　�@　　先ず、　1 次 関 数 　y₁ 　の 直 線 と 2 次 関 数　 y₂　の 曲 線 の 交 点 を求める

　　　　　　　　　　　　　　　　y₁ = y₂　　　x + 2 = x² - 4x + 6

　　　　　　　　　　　　　　　　x + 2 = x² -4x + 6　　　(x + 2) - (x² -4x+ 6) = 0

　　　　　　　　　　　　　　　- x² + 5x - 4 = - ( x² - 5x + 4 ) = 0

　　　　　　　　　　　　　　　　αx　・　βx　=　｛ ５ ± √(25 - 16)　｝ / 2

　　　　　　　　　　　　　　　　　　　　　　　=　｛ ５ ± √9　｝ / 2　 = 　1　，　4　　　　　　　　　　　

　　　　　　交 点の 座 標　　　(αx ・ αy)　　 (βx ・ βy)　　　⇒　　 　( 1 ・ 4 )　　 ( 4 ・ 6 )


　 �A　1 次 関 数 　y₁　で 囲まれた 面 積 　S₁ = αx → βx →βy → αy → αx　の 面 積 を求める

　　　　　　　　　　　　　　　　　S₁= ∫^β_α( x + 2 ) dx =［ ( x² / 2 + 2x ) ］^β_α

　　　　　　　　　　　　　　　　　　= ( 4² / 2 + 2×4 ) - ( 1²/ 2 + 2×1 )

　　　　　　　　　　　　　　　　　　　　　　　　= 16 / 2 + 8 - 2.5 =13.5　

　�B　2 次 関 数　で 囲まれた面 積　S₂ = αx → βx → βy → M →αy → αx　の 面 積 を求める

　　　　　　　　　　　　　　S₂ = ∫^β_α( x² - 4x + 6 ) dx =［ (1/3) x³ - 2x² + 6x ］^β_α

　　　　　　　　　　　　　　　　=［ (1/3) 4³ - 2×4² + 6×4 ］ - ［ (1/3) 1³ - 2×1² + 6×1 ］

　　　　　　　　　　　　　　　　= ［ (4³ / 3 -32 + 24) ］ - ［ 1/3 - 2 + 6 ］

　　　　　　　　　　　　　　　　= 4³ / 3 - 8 - 1/3 − 4 = 4³ /3 - 1/3 - 12 = 9
　　　　　�C　　　従って、　求める 面 積　　　S　= S1 - S2 = 13.5 - 9 = 4.5

　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
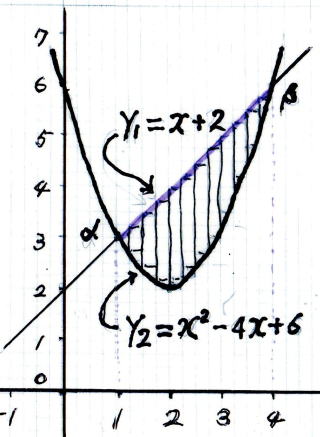
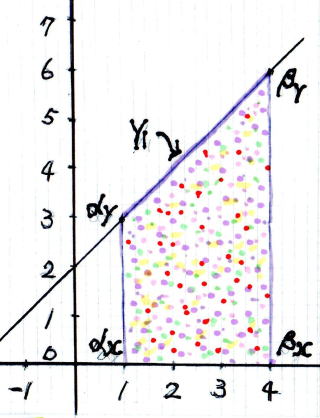
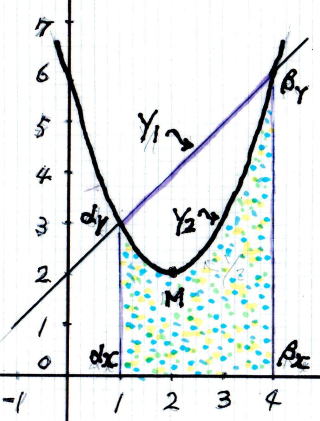
　　　　　　　　　　　　　A　　図 　　　　　　　　　B　　図　　　　　　　　　　　 C　　図



　　　　●　　　最 近 の 計 算 の 仕 方

　　　　　　　　　　　　　　Youtube 　　放 物 線 と 直 線 で 囲まれた 面 積　　　　三輪次男 の ホームページ よ り

A 　図 に示すように1次 関 数y₁ より 2次 関 数 y₂を引いて棒 柱のようにして 区分求積法的 に 積 分 で求める

　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　you tube より

　　　　　　　　　　　上の、画 像に　展 開 式 が示されていますが 見やすく 書き 変え ます。

　　　　　　　　　　　　　　　　　y₁ = x + 2　　　　 y₂ = x² - 4x + 6

　　　　　　　　　　　　　　　　S = ∫^β_α [ ( x + 2 ) - ( x² - 4x + 6 ) ] dx

　　　　　　　　　　［ ］ 内は　　1　次 関 数　 y₁　より　2　次 関 数 y₂　を引いた　棒 柱

　　　　　　　　　　　　　　= ∫^β_α ［ - ( x² - 5x + 4 ) ］ dx

　　　　　　　　　　　　　　= - ∫^β_α ［ ( x - α ) ( x - β ) ］ dx

　　　　　　　　　　　　　　= - ∫^β_α ［ ( x - α ) ( x - α + α - β ) ］ dx

　　　　　　　　　　　　　　　　　　- α + α 　を 挿 入 するのが 味 噌

　　　　　　　　　　　　　　= - ∫^β_α ［ ( x - α )　［ ( x - α) - ( β - α ) ］ dx

　　　　　　　　　　　　　　= - ∫^β_α ( x -α )²dx - ∫^β_α(x - α)( β - α ) dx

　　　　　　　　　　　　 　　　= - ∫^β_α ( x -α )²dx - ( β - α )∫^β_α(x - α) dx

　　　　　　　　　　　　　　　　=　［　1/3　( x -α )³ ］^β_α　-　［　1/2 ( β - α )　(　x - α　)²　］　^β_α

　　　　　　　　　　　　　　　　=　［　1/3　( β -α )³ ］^β_α　-　［　1/2 ( β - α )　(　β - α　)²　］　^β_α

　　　　　　　　　　　　　　　　=　［　1/3　( β -α ) ³ 　-　　1/2　(　β - α　)³　］　^β_α

　　　　　　　　　　　　　　　　 　　　＝　　　( β - α ) ³ / 6　　
　　　　　　　　　　　　　　　　　　S　=　 ( 4 - 1 ) ³ / 6 = 3 ³ / 6　=　 4.5

　　　　　　　【 結 果 】　　　　　　　

　1 次関数 の 直線　と　2 次関数 の 曲線 で囲まれた 面　積 は 直線　曲線 の交　点(α・β) を求めることで

　　　　　　　　　　　　　　　　上式の　簡単な　公　式　で 求める ことができる


　　　　　★　　追 記　−　�@　　　その後 、　Net Surfing　で 関 連 記 事 を 見つけ ました
　　　　　

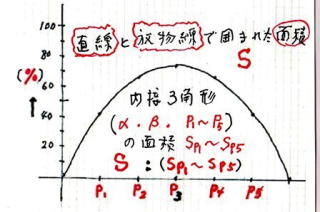
　　　　　『 放物線 の求積法 』 で アルキメデス は、放物線 が 直線 で切られた 部分 の 面 積 が、

　　　放物線 と 直線 の交点 α β と 直線 と 平行 な接 線 が 接触する P 3点 を 頂 点 とする

　　　三角形 の 面 積 の _4/3 倍 になる　ことを 証 明 した。

　　　これは、無限級数 と 公比(en) を用いる。最初の三角形の面積を 1 とし、

　　　この三角形の2辺を割線(en)とし、放物線の隙間に同様な手段で 2つ の新しい三角形を想定すると、

　　　この面積の和は 1/4 となる。これを 無 数 に繰り返して 放物線 の切片を取り尽くすと、面 積 は、

　　　　　　　　　　 　　　

　　　　　　　　　　　　　　　　　　　 　= 1 + 0.25 + 0.0625 + 0.0156 + 0.0039 + = 1.3320 = 4/3　　

　　　 　　　　　　

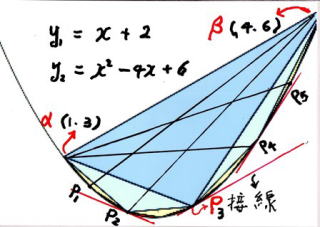
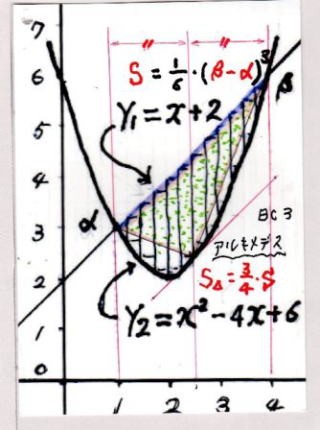
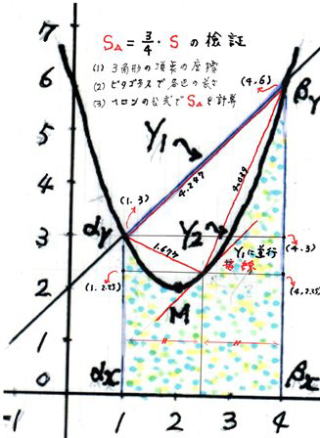
　　　　　　　　　　図　−　1　　　　　　　　　　　　　　図　−　2　　　　　　　　　　図　−　3

　　　　　　図　−　1　　は　　アルキメデス　の　 3 角 形　　( 青色 3 角 形 α β P₃ )

　　　　　　　　　　　　　　　　　　　　　　　 　アルキメデス


　　　　　　　　　　　　　　

　　　　　　ヘロン の 公 式　　T = √｛ s ( s - a ) ( s - b ) ( s - c ) ｝　　　s = ( a + b + c ) / 2


　　　　★　 　追 記 − �A 　　　球 の 体 積　　と　　球 の 表 面 積　　　　またまた　見つけました


　　　　　　　　　球 の 体 積　の 公 式 を 微 分 すると　球 の 表 面 積　の 公 式　となります

　　　　　　　　　更 に 、　球 を 内 接 す る 円 筒 の 側 面 関 と 等 し い

　　　　　　　　球 の 体 積　の 公 式　　V = (4/3) πr³　　　　dV/dr = 4 πr² = 球 の 表 面 積　の 公 式

　　　　　　　　　　
　　　　　　　　また 、　球 の 表 面 積　の 公 式　を 積 分 すると　球 の 体 積　の 公 式　になります

　　　　　　　　　　微 分　と　積 分 は　　陰　陽　　　裏　表　　の 関 係 にあることを 実 感 しました
　
　　　　　　　　　　　　　　　　　　この ペ−ジの　Top　　へ

H ・24 ・ 10 ・ 16　 Up