　　　　　頭の体操　認知症予　防　ボケ防止のために時々暗算をすると良いと聞きました。

　　　　　脳を刺激して脳細胞の劣化防止、抑制に役立つという。

　　　　　　そこで、暗算問題をいくつか準備しました。

　　　　　暗算問題を作るのも頭の体操の一つなので多角的というかできるだけ遠周りの

　　　　　　　ストーリーにしました。　　　　+

　　　　　　　　　　　　アロエの葉

　　　　　　　　　　　　カボチャの花 　　→

　　　　　　　　　　　　ゴーヤの実
　　　　　　　　　　　　　　　　　　　　　　

　　★　　　【暗算問題ー 1 】　　　簡単な足し算

　　　　　　∑ n 　　　n　は　自然数　で　　　1 ・　2 ・　3 ・・・ 10

　　　　　　　　　1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

　　　　　1　から　10　まで足した答えは　55　であることをみな覚えております。

　　　　　　　頭の体操なので答えを忘れたことにして暗算で計算してみます。

　　　　　　　　　　　　　暗算 の仕方には 4 通り程考えられますが、

　　　　　　　以前 My HP に載せたので参照してください。　こちら 【　暗　算　の　問　題　】

　　　　　　　【　暗算　の 問題　】　を開いて　またこのページ　に戻るときは　開いた画面の

　　　　　　左上隅の ← をクリックして戻ってください。外部リンクなので迷子になってしまいます。

　　★　　　【 暗算問題ー 2 】　１月～12月の月々の日数を足して一年の日数を計算する

　　　　　　　　　1月　　2月　　3月　　4月　　5月　　6月　　7月　　8月　　9月　　10月　　11月　　12月　

　　　　　　　　↓　　　　　　　　　　　　　　　　　　　　 ↓　　　　　　　　　　　　　　　　　　　↓　　

　　　　　　　　 31　　 28　　 31　　 30　　 31　　30　　　31　　30　　 31　　　31　　　30　　　31　

　　　　　　　　　30　　 30　　30　　 30 　　・　・　・　・　・　・　・　・　・　・　・　 30　　　30　

　　　　　　±　　+1　　 -2　　+1　　　±0　　+1　　±0　　+1　　±0　　+1　　　+1　　　±0 　　+1　　　　　

　　　　　　　　　　数字を羅列しましたがこの問題は足し算の計算の仕方を工夫します。

　　　　　　　　　　どの問題もそうですが、問題の内容をよく見て特徴点をさがします。　

　　
　　　　　　　　　　この問題では、数列の各項を眺めると 3 0 前後にばらついています。

　　　　　　　　　　そこで、計算の仕方は各項を ( 30 ± α ) として

　　　　　　　　　　∑(m ・day) = 31 + 28 + 31 + 30 + 　・・・・・・・　+ 30 + 31　(m ・day) は　各月の日数

　　　　　　　　　　　　　= (30 + 1) + (30 - 2) + (30 + 1) + 30 + 　・・・・・・・　+ 30 + (30 + 1)

　　　　　　　　　　　 = 30 × 12 + (1 - 2 + 1 + 0 ・・・・・・ + 0 + 1)

　　　　　　　　　　　　= 360 + 5 = 365

　 ★　　【暗算問題ー 3 】　　2　の　等比級数の和を計算する　

　　　　　　　　　　　　　　　∑2 ⁿ　　　n 　はできれば　1 ～ 10　まで

　　　　　　　　　　　　　　ここでは、自分の記憶力テスト用に使ってみる。

　　　　　　　　　　n をどこまで多く計算できるかで自分の記憶力レベルを知る

　　　　　　　　　　∑2 ⁿ　=　2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1024

　　　　　　　　　　　　　2　 6　 14 　30　 62 　126　　254　　510　　1022　　2046

　　　　　　　　　　　私は、　n ＝ 7　の　254　　　　までしかできませんでした

　　 ★　　　【暗算問題ー 4 】　　1/2　の等比級数 の和を計算 する

　　　　　　　　　　　　　　　　∑(1/2)ⁿ　　　　n　は　 1 → ∞　　　　　

　　　　　　　　　　　　　　　　

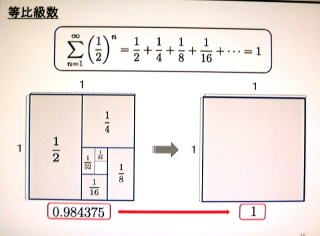
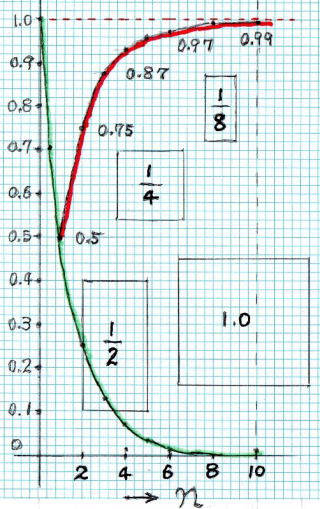
　　　　　　　　∑ (1/2)ⁿ　＝　0.5 +0.25 + 0.125 +0.0625 + ・・・・＝ 1

　　　　　　　　この問題は、暗算　計算するというよりは図形を眺めているほうがよい。

　　　★　　　【暗算問題ー 5 】　ネイピア 数　を 計算 で求める

　　　　　　　　∑1/ n!　　　n　は　0・ 1・ 2・ 3・ 4・ 5
　　　　　　　n!　= n(n-1)(n-2) ・・・ 1　　但し　0 ! = 1　(!=　階乗)

　　　　　　　　　　　

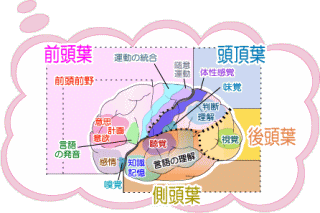
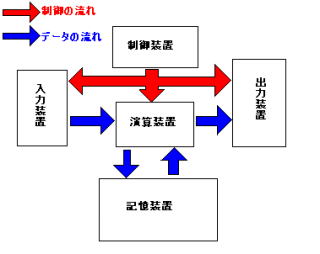
　　　　　　　　　　　　脳 の構造　　　　　　　　　　　　　cluster memory

　　　　　　　　　　　　　　　　

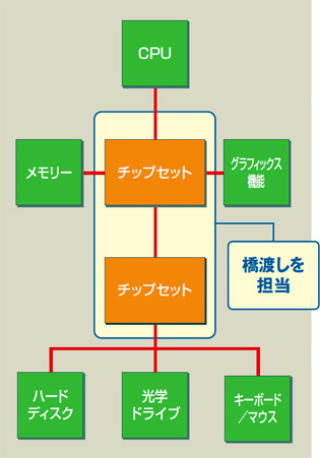
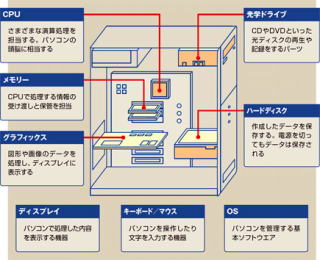
　　　　　　　　　　　　　　　　　　　　　パソコン　の構成

　　　　　　　ここで、人間の脳とパソコンを比較してみると、両者の機能はよく似ております。

　　　　　　　　　(計算する)　(暗算する)　ときの (脳の働き方) をイメージしてみます。

　　　　　　暗算しているときの脳の働きは、 3 っの機能を同時に並行して実行しております

　　　　　　指令機能 ( 計算しなさい、記憶しなさい、表示しなさい　等　パソコンの CPU　集中制御機能 )

　　　　　　　　計算機能、記憶機能 (一時的記憶　temporary me,ory ) 、の 3 っです。

　　　　　　暗算の計算では計算をしながら部分部分を記憶しながら進行していきますが、

　　　　　　人間の脳の記憶容量は小さいので計算容量が大きくなると記憶容量オーバーとなり

　　　　　　計算を断念せざるえなくなります。

　　　　　　　私は、脳の記憶容量を大きくする工夫をしてみました。

　　　　　　　　　上の画像に示す　cluster　memory　( ぶどう　の　房 )　です。

　　　　　　脳をぶどうの一粒～のように小分け (小区分)にします。この小区分に計算途中の部分記憶を

　　　　　　保存します。　この　小分け　(小区分)　を　cluster memory　 cm-1 cm-2 ・・・・　と名づけます。

　　　　　　　　記憶の呼び出しが小分けしてあるので容易になります。

　　　　　　　　　　　　　下の、計算例で説明します。

　　　　　　計算式のアンダーラインの部分をそれぞれ cm-1 cm-2 cm-3 に保存するやり方です。

　　　　　　　　∑1 /n ! = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120

　　　　　　　∑1 /n ! = (1 + 1) +(1/2 + 1/6) +(1/24 + 1/120)

　　　　　　　　= 2 + 2/3 +1/20 =2 + 0.66 +0.05= 2 + 0.71 = 2.71 = e
　　　　　　　　　　e　は　ネイピア数　　対数の底　　　　
　　　　　　　　　eは少数点以下無限に続く無理数である。
　　　　しかも、無理数の中でも数少ない超越数です。

　　　★　　【暗算問題ー6 】　　　平方根の 和

　　　　　　　　　　　∑√n = √1 + √2 + √3 + 　・・・・・　 + √9 + √10

　　　　　　　　　　　　 √1 = 1.000

　　　　　　　　　　　　√2 = 1.414 　21356　　　　一夜一夜　に人見ごろ

　　　　　　　　　　　　√3 = 1.732 　0508075　　　人並みに　おごれやおなご

　　　　　　　　　　　　　√4 = 2.000

　　　　　　　　　　　　√5 = 2.236 　0679　　　　　　富士山麓　オーム鳴く

　　　　　　　　　　　　√6 = 2.449 　4897　　　　　浪人よ良く　失敗苦難

　　　　　　　　　　　　√7 = 2.645 　7513110　　　　風呂で死後　の名残り勇んで 110番

　　　　　　　　　　　　√8 = 2.828 　427　　　　　にやにや死にな

　　　　　　　　　　　　√9 = 3.000

　　　　　　　　　　　　√10 = 3.162 　27766　　　　Get (3)　 a (1) 　pistol (6) 　to (2) 　me (2).

　　　　　　　　　　　　英語では語呂合わせの代わりにアルファベッツトの文字数で表します。

　　　　　　　　　∑√n = √1 + √2 + √3 + ・・・・・・ √9 + √10 =　 22.466

　　　　　　　　　　この問題も暗算、計算というよりも一桁の数字の平方根を語呂合わせで覚えることです。

　　　　　　　　　　　　　　　　　　　　　　　このページの　Top　へ

　