(√5−1)/2 〓 0.618 の黄金比 に近づくことを揚げた.
この黄金比の逆数の 小数点以下の部分が 黄金比と同じになるのもおもしろい.
1/0.618 〓 1.618
フィポナッチ数列をもう一度揚げておく
1、1、2、3、5、8、13、21、34、55、89、144、−−−−−−
先行する2項の和が 次ぎの数となることから、1、1、2、3、くらいを覚えておけば
その後の数は暗記する必要はない.また隣り合う2項間の比が 0.618 黄金比
フィポナッチ数列は自然のいたるいたるところに出現するという.
☆ 一本の枝に生える葉の数も フィポナッチ数列 に対応している.
☆ 花にも出てくる.
ほぼすべての花について、花弁の数は3、5、8,13,21,34,55,89
のいずれかとなる.ユリは3枚の花弁をもち、キンポウゲは 5枚、ヒエンソウは多くの
場合8枚、マリゴ−ルドは 13枚、アスタ−は 21枚、ディジ−は普通 34枚か
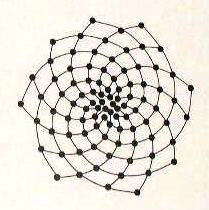
55枚か、89枚である.ヒマワリにも現れる.ヒマワリの頭部にある小花は一つは
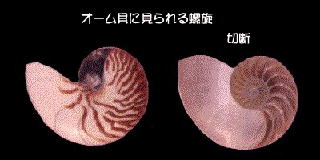
時計まわり、他方は反時計まわり方向の 二組の螺旋状 に配置されている.
時計まわり方向の螺旋の数はしばしば 34本であり、反時計方向の螺旋は 55本で
ある.それらの数は 55本と89本 のこともあれば、 89と144本 のこともある.
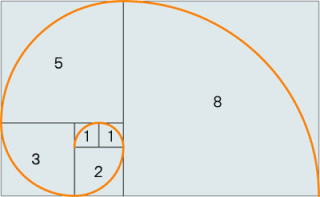
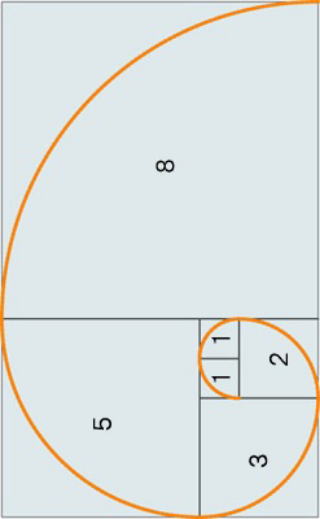
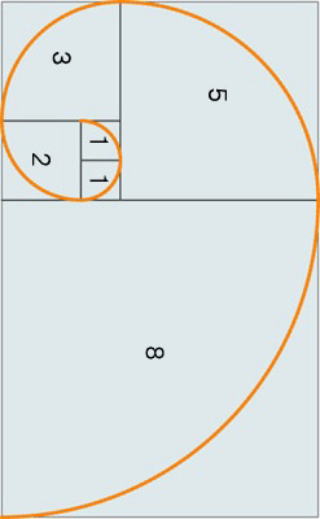
☆ タテとヨコの辺の比が黄金比(0.618)となるような長方形
その長方形は正方形と もう一つの長方形に分割できる.
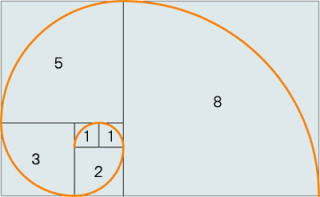

図のように二番目の長方形は最初の大きな長方形と相似ある.長方形の列の対応する
頂点を結んで描いた螺旋形は、貝殻にもよく見られる形という.
☆ 黄金比は芸術の世界にも “ 美の古典的理想 ” として現れる.
この数列にはどこか神聖なところがあるようで、今日も活動しいるフィポナッチ協会
はカリフォルニア州のセント.メアリ−ズ.カレッジに本拠地を置いている.
この協会は、黄金比はこの世に与えられた神の贈物だとという信念にもとづいて、
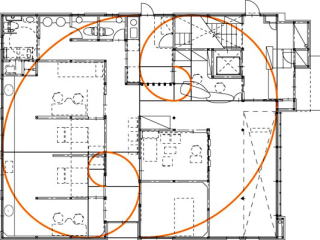
自然や芸術や建造物の中に黄金比とフィポナッチ数列の実例を探し出すことを使命としている.
沢山の事例が集められているようです.
☆ 黄金比を探し求めているある人が何組かの夫婦にたのんで
妻のヘソまでの高さ と 身 長 を
測ってもらった.ヘソまでの高さを身長で割ったら 黄金比の 0.618 に
近かったという.ちなみに我が山の神にはかってもらったら少し外れていました.
笑い話でしょうか
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆