sub - 13

ギリシャ の ３大 難 問　 つづき

３ 大難問 の 一つ　　［ 角 の 三 等 分 問 題　］

　　任意の与えられた 角 を　３ 等 分 せよ

　（ただし、コンパス と 目盛りのない 定 規 を使う）　

右上図　 のような ヒント 図 がありました。　説 明 がなかったので

どのような 手 順 で ３ 等 分 するのか　わかりませんでした。

ところが　net surfing　していたらたまたま

左 図 のような 小 道 具 を見つけました。

　　　　三 等 分 定 規 です。

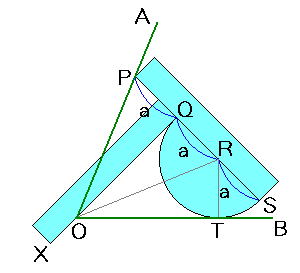
　　　　　　　　〔 三 等 分 定 規 　の　使 い 方 〕


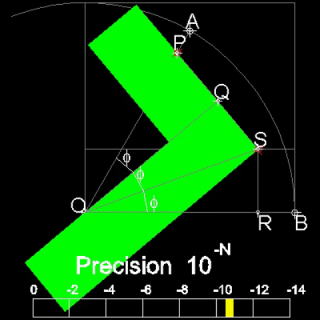
　与えられた 任 意 の　角　∠AOB　を　三等分定規　に　P. O. T　が 接するように

　　　　　合 わ せ る。

　　図 示　三等分定規 は　PQ . QR . RS　の 距 離 が　a　と 等 間 隔 にしてある。

　　　　　　　　更 に、R　を 中 心 とする 半 円 の 半 径 も　a　です。

　　　　　　　　　　　　　　　　　従って、 △POQ 　と　△QOR　は 合 同 で あ る。

　　　　　　　　　　　　　　　　更　 に、 △QOR　し　△ROT　も 合 同 で あ る。

　　　　　　　　　　　 　　　∠ AOB 　は　 　三 等 分　 　さ れ ま し た。



☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆　

★ １０１ ★　　　角 の 三 等 分 　定 規

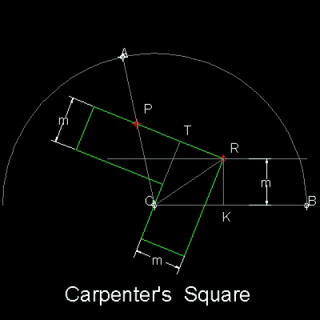
★ ２０２ ★　　　Carpenter’s　　Square　　　　　大工用　直角 定規


　　　　　　　　１９２８年　アメリカ の 数 学 誌 （ American Mathematical Monthly ）

　　　　　　　　　に　大工用 直角 定規　による ［ 角 の ３ 等 分 ］　が 発 表 された。

　　★ ３０３ ★　　［ コンパス と定 規 ］による 任 意 の 角 の ３ 等 分 法

　　　　　　　　　The trisection of an angle withruler and compass.

★ ４０４ ★　 　［コンパスと二箇所に印のついた定規による 角の３等分］

　［ 使　い　方 ］　

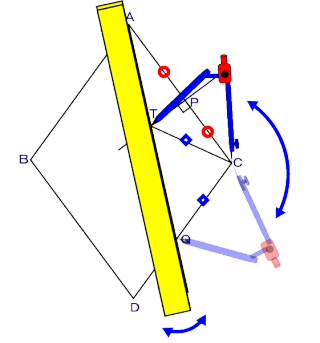
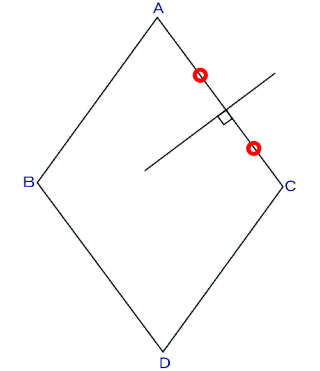
　右 図　記 号 に従って 説 明 します
　
　●　三等分する 角 を AOB　とする

　●　直角 定規 の 幅 は 両 方 とも m　とする

　　　　　［ 手 順 図　 �@〜�E　に 従って 説 明 します ］

　　　　　　　　　　　　　　　　　　　　　　　　　手　順　　�E の　拡　大　　→

　　　　◆　　手　順　　　�@　　　与えられた 任意 の 角　 ∠ BAC

　　　　◆　　手　順　　　�A　　　平行四辺形 を 作る

　　　　　　作り方　コンパスで点 B を中心に半径 AC の 円 弧 を書く

　　　　　　一方、点 C を中心に半径 AB の 円 弧 を書く、その交点を D と

　　　　 　する 　　B-D　を結ぶ C-D　を結ぶ と 平行四辺形 となる　

　　　　◆　　手　順　　　�B　　　辺 AC に　垂直 ２ 等分線 を 立てる

　　　　　垂直２等分線 の 立て方　　点 A 及び点 C を中心に適当な半径の

　　　　　円 弧 を書く　円 弧 の交点 ２つ を結べば　垂直　２等分線　となる

　　　　◆　　手　順　　　�C　　与えられた角　の　３ 分 の １　角　を作る

　　　　　定規の一辺が点 A を基点に 垂直二等分線　上　点 T と

　　　　　線 分 CD 上の 点 Q と が交わるように置く　

　　　　　C-T ＝ C-D　となるように 定 規 を 動かす

　　　　　コンパス で 点 C を中心 に 円 弧 を描いたとき T と Q が同時に

　　　　　交わるように 定 規 を 調 整 すればよい 　

　　　　　コンパス は C-T と C-Q の 長さ の 同 期 を取るために 使 用 します

　　　　　�E　の　拡大図　を　参照　　　この 操 作 が この 問 題 の ポイント です


　 【 この図で、与えられた角の《 １／３角∠CAQ 》が得られました 】

　　　♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪　　　

●　内 側 の 辺 の 延 長 が 外 側 の 辺 と

　　 交わる 点 を T とする

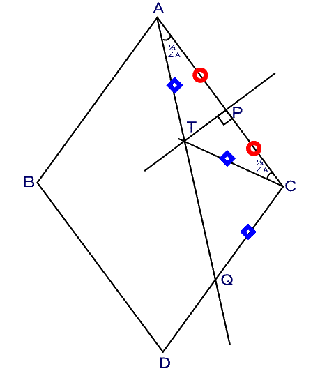
　　外 側 の 辺 の 交 点 を　Ｒ　とする

　　点 R と T の 距 離 を m とする

●　外 側 の 辺 上 に R から 2 m の

　　幅 の 距 離 に 点 P の 目 印 を 付 ける

●　この 定 規 を使って OB から m の 幅 の 平 行 線 を引く

●　定 規 の 内 側 の 辺 が 点 0 を通り、コーナー R がこの平 行 線 上 を動くように　定 規 を 動 かす

　　点 P が 線 分 OA の上 に来たとき R と O を 結ぶ線 が ∠AOB の ３ 等 分 線 になっている


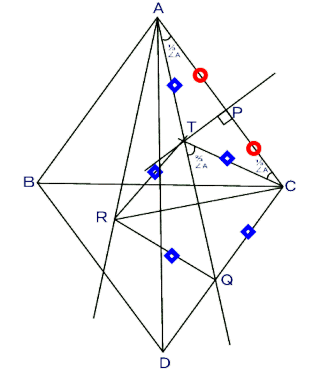
　　　　　　　［ 理 由 ］　　　△OPT，　△ORT，　△ORK　は　合 同　である



◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎◎

〔　角 の 3 等 分　 手 順 図　］　　　　　�@ 〜 �E

�@

�A

�B

�C

�E

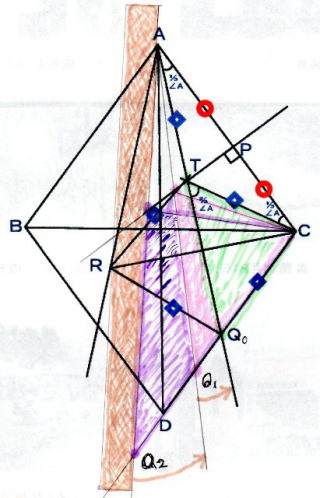
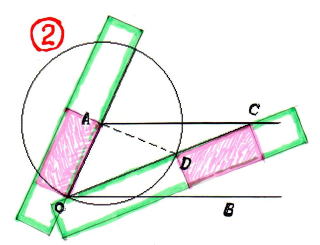
　　◆　　手　順　　　�E　　拡 大 図　で　全 体 説 明


　　　　この図 ができれば後は、三角形 の 定 理、 平行四辺形 の 定 理　等の

　　　　　おきまりの 幾 何 学 の 勉 強 となります。


　　∠CAT ＝ θ　とする。　　 △TCA　と　 △CTQ　が共に　二等辺三角形でありから

　　　 　　　　∠CQT ＝ ∠CTQ + ∠ACT ＝ 2 θ

　　　　　　 線 分 AB　と 線 分 CD　は 平 行 だから、

　　　　　　　∠BAT ＝ ∠CQT ＝ 2 θ　　　　よって

　　　　　　　　∠BAC ＝ ∠BAT + ∠CAT ＝ 3 θ

　　　　　　　　　　　　∴　∠BAC ： ∠CAT ＝ 3 ： 1


◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆

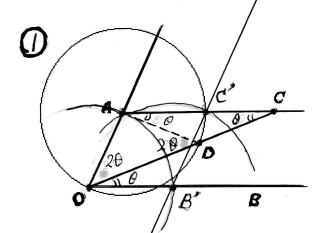
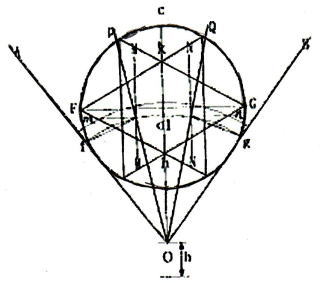
アルキメデス　による　方 法　といわれいおります

〔　説　明　〕

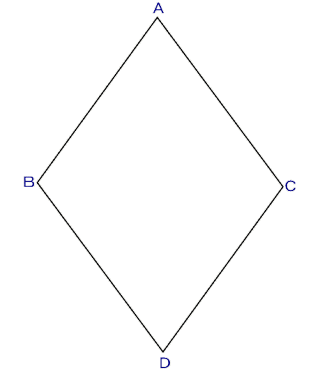
　　　　▼　　与えられた角を ∠AOB　とする。　　 OA　は 定 規 の二カ所の印の長さ にとる

　　　　　　　　点　A　から OB 　に 平行線 を引く
　　　　　　　 　A　を中心として、半径 OA の 円 を描く

　　　　▼　　先に A　から引いた平行線上に点 C　をとり、OC との 交点 を D とするとき、
　　　　　　　　CD　が OA　と 等しい長さ になるようにする

　　　　▼　　このとき　　OA ＝ AD ＝ DC であるから ∠ACD ＝ ∠CAD ， ∠ADO ＝ ∠AOD
　　　　　　　　明らかに　∠AOD ＝ ∠ADO ＝ ∠ACD + ∠CDA ＝ 2 ∠ACD

　　　　　　　一方 錯 角 で　∠BOC ＝ ∠ACO ＝ ∠ACD
　　　　　　　よって　∠AOB ＝ ∠BOC + ∠AOD ＝ ∠ACD + 2 ∠ACD ＝ 3 ∠BOC

　　　　　　　　　　　　　　即ち　三 等 分　できたわけである。

　　〔 注 〕　　平行線 の引き方と，CD の長さと AO の長さ を等しくとる 方 法 は

　　　　　　　 　 補 助 線 を入れておいたので 参 考 にしてください。

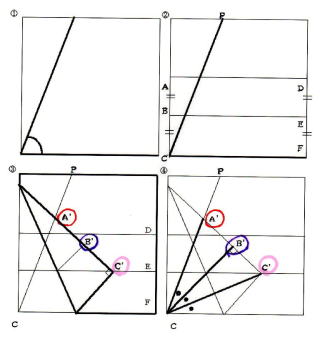
　　　★ ５０５ ★　　　〔 折 り 紙 を 使った 角 の 三 等 分 〕


　　　　　　コンパス と 定 規 のみを用いて任意の 角 の 三等分 はできないが、

　　　　　　　　　　折 り 紙 を用いると、０ 度 から ９０ 度の任意の 角 の 三等分 は

　　　　　　　　　　可能であることが知られている。

　　　　　　　　　　但し、折　り　紙　とは、一辺の長さが　１０ �p　の 正方形 とする。


　　　 　　�@　折 り 紙 を適当に折って、任意 の 角 を作くる。

　　　　　�A　同じ間隔で ２ 回 折り、折 り 目 をつける。

　　　　　�B　A が PC 上 A‘、C が BE 上 C’ になるよおに折り、折 り 目 をつける。

　　　 　　�C　A’ C’の中点 B’に関して、A’ B’ と　C’ B’が重なるように折ると、その 折り目 は C を通る

　　　　　�D　�C において、CB’　、　CC’が 角 の 三等分 を与えている。

　　　　　　　　 　　　　　（　�A　と　�B　が、角 の 三 等 分　の　ポイント　である　）