

お遊び の 数学 (そのー2)
s - 19
頭の体操として数学問題の計算を暗算で行い脳細胞を刺激して認知症予防、
ボケ防止にやくだてます。
なお、お遊びなので数学の問題を計算で求めることを手品、Magic になぞらえて
計算は 手品 の 種明かし とします。
( 例 題 ) 自然対数 y = logex の底 e (ネイピア数) を計算で求める
e = 2.71828182845905 鮒 一鉢 二鉢 一鉢 二鉢 至極 美味しい
★ 【 Magic - 1 】 e = 1 +1 + 1/2 + 1/6 + 1/24 + 1/120 + ・・+ 1/( 1・2・3・・ n ) ①
( 種 明かし ) 上式の生まれをたどる
関 数 は 無 限 級 数 で表せる y = f (x) = ∑an ・ xn n = 0 → ∞
y = f (x) = a0 + a1・x1 + a2・x2 + a3・x3 + ・ ・ + an・xn ②
f (x) = ex とすると
y =f (x) = ex = a0 + a1・x1 + a2・x2 + a3・x3 + ・ ・ + an・xn
x = 0 とおくと f (0) = e0 = 1 = a0 よって a0 = 1
ex は 微 分 しても 積 分 しても 変わりません
y = ex = y ′= (ex) ′= ex
y′= f (x) ′= (ex) ′= a1 + 2a2x + 3a3x2 + ・・・ + nanxn-1
x = 0 とおくと f (0)′ = e0 = 1 = a1 よって a1 = 1
y ″= f (x) ″= (ex) ″= 2a2 + 3・2a3x + ・・・ + n(n-1)anxn-2
x = 0 とおくと f (0)″ = e0 = 1 = 2a2 よって a2= 1/2
y3′= f (x) 3′= (ex) 3′= 3・2a3 + ・・・ + n(n-1)(n-2)anxn-3
x = 0 とおくと f (0)3′= e0 = 1 = 3・2a3よって a3 = 1/3・2
以下 同様にこれを続けます
前記、無限級数 ② 式に a0 a1 a2 a3 ・・・ を代入して、更に x = 1 とすると
① 式 e = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + ・・・・・+ 1/n!
= 1 + 1 + 0.5 + 0.166 + 0.041 + 0.008 + ・・・・= 2.718281828
が 得られます
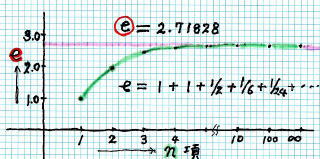
無限級数 の 第 n 項 まで足したときの e の値を グラフ に描く
★ 【 Magic - 2 】 e = 2.71828 は y = logax を微 分 した答 え の中 に現れます
( 種 明かし ) y = logax を 微 分 する 展 開 式
dy/dx = lim△x→0〔 loga(x + △x) - logax〕 / △x
= lim△x→0(1/△x) loga(x + △x) / x
= lim△x→0(1/△x)loga(1 + △x/x)
△x/x = h とおくと △x = hx
= limh→0(1/hx)loga(1 + h)
= limh→0(1/x)loga(1 + h) 1/h =(1/x) logae
a = e のとき y ′= dy/dx = (logex) ′= 1/x
e= limh→0 ( 1 + h ) 1/h = 2.71828
なお、 △x/x = 1/k とおくと △x = x/k
e = limk→∞(1 + 1/k)k = 2.71828
h および k に いろんな数 を入れて計算した結果をプロットしてグラフ を描く
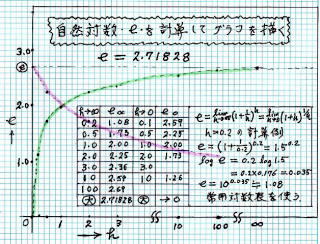
頭の体操 数学の問題を、手品 Magic として 表現してみました
お遊び とはいえ、少し品がないといわれましょうか
この ページ の Top へ
♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪

一次方程式 の 直 線 と 二次方程式 の 二 次 曲 線 で 囲まれた 面 積 の 公 式
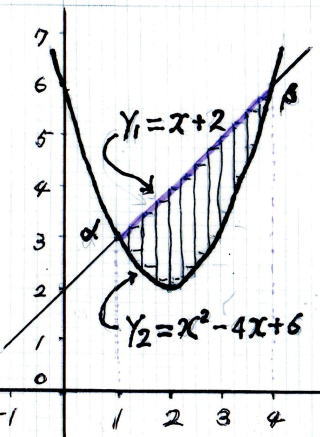
y1 = a x + b y2 = c x2 + d x + e
y3 = y1 - y2 = (a x + b) - (c x2 + d x + e) = - c x2 + (a - d) x + (b - e)
α = - 1/2c 【 - (a - d) +〔 (a -d)2 - 4 ( - c) (b - e) 〕1/2 】
β = - 1/2c 【 - (a - d) -〔 (a -d)2 - 4 ( - c) (b - e) 〕1/2 】
二次方程式 y3 = -c x2 + (a - d) x + (b - e) の 解 α β は
一次直線 y1 と 二次曲線 y2 の 共有点 交点 である
S = (β - α) 3 / 6
= 《 - 1/2c 【 - (a - d) -〔 (a -d)2 - 4 ( - c) (b - e) 〕1/2 】
- 1/2c 【 - (a - d) +〔 (a -d)2 - 4 ( - c) (b - e) 〕1/2 】 》 / 6
この 公 式 を導く 展 開 式 を以下に記します
積分して閉曲面の面積を求める公式