

三次方程式 の お 勉 強
s - 21
三次方程式 に 関して はこれまでにも 勉 強 して My HP Up してきました。
高校時代 に 三次方程式 は あまり 勉 強 しませんでした。 補 充
していきます。
● 三次方程式 の 解 フォンタナ ・ カルダノ の 公式
( My HP ) 外部リンク t-miwa2
http://members.jcom.home.ne.jp/t-miwa2/newpage65.htm
● 三次方程式 の 練習問題 解 と 係数 の 関係式 を作る
外部リンク t-miwa2
http://members.jcom.home.ne.jp/t-miwa2/newpage79.htm
● 四次方程式 の 解 展開式 の 項 数 が 多くて 目眩 がします
外部リンク t-miwa3
http://members.jcom.homene.jp/t-miwa3/4jieq.html
● n 次方程式 の お 遊 び 外部リンク t-miwa3
http://members.jcom.home.ne.jp/t-miwa3/cubiceq.html
★ 三次方程式 の 極 大 ・ 極 小
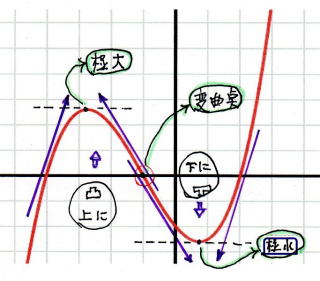

★ 三次方程式 の 変 曲 点
変 曲 点 とは、関 数 の 凹 凸 が 変 化 する 点 をいう
三次方程式 は 変 曲 点 を 一つ 持つ。
y = ax3 + bx2 + cx + d
変 曲 点 は 関 数 y を 二階 微分 して y〝= 0 のときの ( x ・y ) 座 標 として求まる
y ' = 3 a ・ x2 + 2 b ・ x + c y " = 6 a ・ x + 2 b = 0 x = - b / 3 a
y に x = - b / 3 a を代入して y = a ( -b/3a )3 + b ( -b/3a )2 + c ( -b/3a ) + d
y = ( 2 b3 - 9 abc + 27 a2d ) / 27 a2
変 曲 点 の 座 標 は x = - b / 3a ・ y = ( 2 b3 - 9 abc + 27 a2d ) / 27 a2
【 y = x3 - 3 x2 】 の ときの グ ラ フ
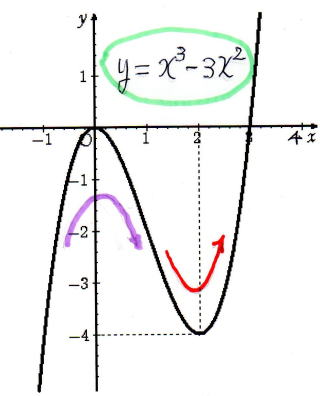
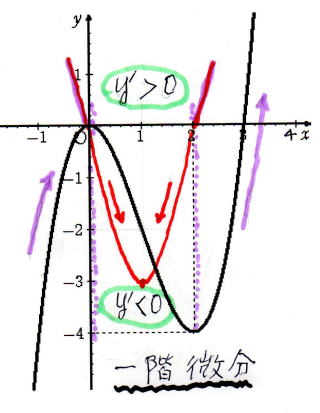
関 数 y = x3 -3 x2 を 一階微分 ・ 二階微分 して分かること
● 一階微分 のとき y ' は 二次方程式 y ' = 3 x2- 6 x
y ' > 0 のとき 関 数 y の 曲 線 は x < 0 及び x > 2 で 単 調 増 加 ↑
y " < 0 のとき 関 数 y の 曲 線 は 0 < x < 2 で 単 調 減 少 ↓
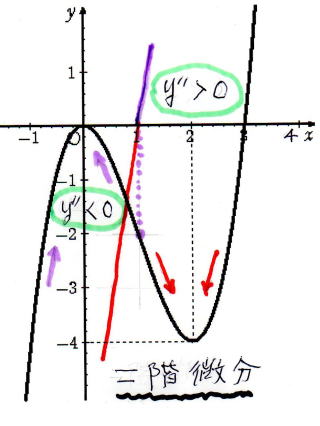
● 二階微分 のとき y " は 一次方程式 y " = 6 x- 6
y " = 0 のとき 曲 線 の 変 曲 点 x = 1 y = - 2
y " > 0 のとき 関 数 y の 曲 線
は 下 に 凸
y " < 0 のとき 関 数 y の 曲 線
は 上 に 凸
変曲点 ・極大値 ・極小値 には 次の ような 性 質 ・ 特 徴 がある
① 変曲点 は 極大値 と 極小値 の 中点 にある
② ( 極大値 と 変曲点 の x座標 の 差 ) と
( 変曲点 と 極小値 の x座標 の 差 ) は等しい
③ ( 極小値 と 変曲点 のy 座標 の 差 ) と
( 変曲点 と 極大値 の y 座標 の 差 ) は等しい
★ 代数方程式 の判 別 式
代数方程式 が与えられたとき、異なる 実数解 を持つのか、重 解 を持つのか、それとも
異なる 虚数解 を持つのかを 判別する式 を 代数方程式 の 判 別 式 と 呼びます。
n 次多項式 F (x) = a0 xn + a1 xn-1 + ・・・・ + an-1 x + an
方程式 F (x) = 0 の 根 を、 α1、α2、 ・・・・ αn とする
【 代数学 の 基本定理 】
n 次方程式 は 複素数 内に 、重 根 を含めて n 個 の 解 が 存在する
この α1 ・ α2 ・・ αn の異なる i 、j すへぼての、根 の 差 分 の 平 方
( αi - αj ) 2 の 積 を考えて
P 2 = П (αi - αj) 2 = (α1 - α2) 2 (α1 - α3) 2 ・・・ (α1 - αn) 2
×(α2 - α3) 2 (α2 - α4) 2 ・・・ (α2 - αn) 2
・・・・・・・・・・・・・・・・・・・・
×(αn-1 - αn) 2
もし 、 重 解 を持つとすれば、 p 2 に含まれる 括 弧 のうち、どれかが 零 になり、
p2 は 零 になるはずです。 逆に、p2 が 零 でないのは、全ての 解 が 異なる 場合だけです。
なお、p 2 二乗 が 負 になれば、共 役 な 虚数解 が 奇数 組 含まれているということです。
方程式 F (x) = 0 判 別 式 D = a02(n-1) П ( αi - αj) 2
D = 0 ならば 重 解 D > 0 ならば 異なる 実 数 解 D < 0 ならば 異なる 虚 数 解
● 二次方程式 の 判 別 式
a x 2 + b x + c = 0 の場合 解 を α β とおくと
解 と 係 数 の 関 係 から α + β = - b / a α β
= c / a
判 別 式 D = a 2 (α - β) 2
= a 2 { (α + β) 2 - 4αβ } 注 ; 完成平方 ( ◎◎◎ ) 2 = 実 数
チルンハウス 変 換 ともいう
= a 2 { b 2 / a 2 - 4 c / a } = b 2 - 4 a c
● 三次方程式 の 判 別 式
a x 3 + b x 2 + c x + d = 0
判 別 式 D = b2c2 + 18 abcd - 4 ac3 - 4 b3d - 27 a2d2
判 別 式 を 作る
3 次方程式 に x = x - b / 3 a を代入して チルンハウス変換 立体完成 する
展 開 式 は 長 く なるので 一 部 省 略 します
a x3 + b x2 + c x + d = 0 ⇒ x3 + p x + q = 0
p = c - b2 / 3 a q = - b3 / 27 a2 + b3 /9 a2 - bc / 3 a + d
a x3 + b x2 + c x + d = 0 の 3っ 解 を α、β、γ とおくと 、解 と 係 数 の 関 係 から
α + β + γ = 0 、 αβ + βγ + γα = p
、 αβγ = - q
判 別 式 は D = (α - β) 2 (α - γ) 2 (β - γ) 2 なので
ここで、 (α - β) (β - γ) = α2 - (β + γ) α + βγ
β + γ = - α --------→ = α2 - (- α) α + p - (αβ + γα)
β γ = - (αβ + γα) --→ = α2 + α2 + p - (β + γ) α
= 2α2 + p - (- α) α
= 3 α2 + p
同 様 に 、 (β - γ) (β - α) = 3 β2 + p (γ - α) (γ - β) = 3 γ2 + p
これらの 3 式 を 辺 々掛 け ると、
- (α - β) 2 (α - γ) 2 (β - γ) 2
= (3α2 + p) (3β2 + p) (3γ2 + p)
= p3 + 3 (α2 + β2 + γ2) p2 + 9 (α2β2 + β2γ2 + γ2α2) p + 27 α2β2γ2
ここで α2 + β2 + γ2 = (α + β + γ) 2 - 2 (αβ + βγ + γα) = - 2 p
⇒ 0 ⇒ p
α2β2 + β2γ2 + γ2α2 = (αβ + βγ + γα) 2 - 2 αβγ (α + β + γ) = p2 なので
- (α - β) 2 (α - γ) 2 (β - γ) 2 = p3 - 6 p3 + 9 p3 + 27 q2 = 4 p3 + 27 q2
したがって、 3次方程式 x3+ p x + q= 0 の
判 別 式 D = - 4 p3 - 27 q2 が 得 ら れ ました
★ 三次方程式の因 数 分 解
● 三次方程式 の 解 を 因数分解 で 求める
① x3 - 1 = 0 ② x3 - a3
① の場合 ( x3 - 1 ) / ( x - 1 ) = ( x2 + x + 1 )
( x3 - 1 ) = ( x - 1) ( x2 - x + 1 ) = 0
x - 1 = 0 x2 + x + 1 = 0
x1 = 1 x2 = { - 1 + √( 1 - 4 x 0 ) } / 2 = { - 1 + i √3} / 2
x3 = { - 1 - √( 1 - 4 x 0 ) } / 2 = { - 1- i √3 } / 2
x2 = ω x3 = ω2 と 表 す こともある ω2 = 【 { - 1+ i√3} / 2 】 2
② の場合 ( x3 -a 3) / ( x -a3 ) = ( x2 + x + 1 )
( x3 - 1 ) = ( x - 1 ) ( x2 - x + 1 ) = 0
x - a = 0 x2 + a x + a2 = 0
x1 = a x2 = { - 1 + √( 1 - 4 x 0 ) } / 2 = a { - 1 + i √3} / 2 = ω ・ a
x3 = { - 1 - √( 1 - 4 x 0 ) } / 2 = a { - 1 - i √3 } / 2 = ω2 ・ a
【 注 】 三次方程式の解の公式 カルダノの公式 展開式 説明の中に
三次方程式 の 3 っの 解 の求め方に、この 因数分解 で 求める方法 を 引 用 しています
● 三次方程式 の 解 と 係 数 の 関 係
x3 + a x2 + b x + c = 0 解 を α ・ β ・ γ とする
解 と 係 数 の 関 係 の 式 を 因 数 分 解 によって 求める
上の三次方程式 は (x - α) (x - β) (x -γ) = 0 となる
【 x2 - (α + β) x + αβ】 ・ (x -γ) = x3 - (α + β + γ) x2 + (αβ + αγ + βγ) x - αβγ = 0
三次方程式の 【 解 と 係 数 の 関 係 式 】 ができました
a = - ( α + β + τγ ) b = ( αβ + αγ + βγ ) c = - αβγ
ちなみに、 三次方程式 の 解 を α β γ を 1 ・ 2 ・ 3 としたとき
上の関係式を使って x3 - 6 x2 + 11 x - 6 = 0 となる
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
この ページ の Top へ
H 24・09・25 Up