sub - 8
お遊び の 数学 ( 頭 の 体 操 )
自然 対数 の 底 e を計算してみる
e の計算方法には 2 通り あります
一つは、指数 関数 を 無限 級数、テーイラー 展 開 して 求める
もう一つは、対数関数 を 微 分 したとき、その 解 の 式 に 現れます
![]() 指数関数 を テーイラー展開 して求める方法
指数関数 を テーイラー展開 して求める方法
f(x) = Σ[〈f(n)(a)〉/n!](x-a)n n = 0 → ∞ n! = 1×2×3・・・×n
a = 0 のとき Σ[〈f(n)(0)〉/n!] xn マクローリン展開 という
f(x) = e x = 1 + (1/1!)x +( 1/2!)x2 + (1/3!)x3+ ・・ + (1/n!)xn + ・
この展開式は ex が 微分しても、積分しても ex となる 特徴が生かされている
ここで x = 1 とすると e1 = e で e の値が計算できます
f(x) = e1 = e = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + ・・・・・
e = 1 、 2 、2.5 、2.666 、2.674、 ・・・・・・ 、2.71828 ・・・・・
展開式の 弟 n 項 まで足したときの e の値は n を大きくしていくほど e の近似値の
正しい桁数 は多くなる
e = 2 .71828 18284 59045 23536 02874 71352 ・・・・・・
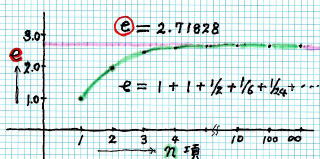
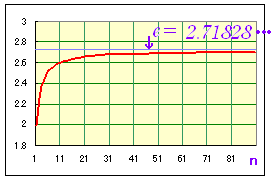
e = 2.71828 に 収 束 する 曲 線
![]() 対数関数 を 微分したときの 解の式 の中に現れる e
対数関数 を 微分したときの 解の式 の中に現れる e
対 数 関 数 f(x) = log a x
f’(x) = (log a x)’ = lim 〔log a (x + △x) - log a x〕 / △x
= 1/Δx ・lim 〔log a (x + △x) - log a x〕 △x → 0
= 1/△x ・lim log a (x + △x) / log a x
= 1/△x ・lim log a 〔(x + △x) / x〕
= 1/△x ・lim log a (1 + △x / x )
ここで △x / x = h or △x/x = 1/ h とおく
h → 0 h → ∞
= 1/( x .h) lim log a (1 + h )
= 1/ x .lim log a (1 + h) 1/h = 1/x.lim log a (1 + 1/h)h = 1/ x ・log ae
( 1 + h ) 1/h = e = 2.71828 = ( 1 + 1/h )h
h → 0 無 限 小 にしたときと h → ∞ 無 限 大 にしたとき
同 じ e = 2.71828 に 収束する ことに 驚 き ました
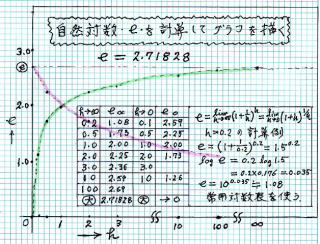
計 算 結 果 を グラフ に描いてみました
![]() 対 数 e の 歴 史
対 数 e の 歴 史
対 数 e は 17〜18 世紀頃 に 世界 の 数学者達 に 発 見 され、育てられてきました。
対 数 e = 2.71828 は ネイピア数 と呼ばれる 数学定数 の一つです。
最初に世に公表されたのが1618年 ネイピア の著書 “ 対数の研究の付録 ”に表として
載せられました。
はじめてネイピア数をそのものを見いだしたのは ヤコブ.ベルヌーイ だとされています。
lim .〔1 + (1/n)〕n n → ∞ 利子 の 複利計算 との 関 連 で言及されていたという。
日本では同時期、1720年頃に、和算家 建部賢弘 によって テイラー 級 数 が使用されている。
正1024角形 のみを用いた 40 桁程度の 円 周 率 を導き出している。
π2 = 9 〔 1 + 12 / 3.4 + (12 + 22)/ 3.4.5.6 + (12 - 22 + 32)/ 3.4.5.6.7.8 +
実質は ( sin-1 x ) 2 / 2 の 級 数 に x = 1/2 を代入したもの
鎖国時代のこと西欧文化が日本に導入されることはないので建部自身が、これが テイラー 展開 の
一つ とは知る由もなかったことでしょう。
建部賢弘 は和算家として世界的に有名な 関 孝和 に師事、将軍 吉宗 に 関 孝和 共々
認められて優遇されたとのことです。
ここで敢えて日本の数学者を引き合いに出したのは別々の国の人間がほぼ同時期に、交流もなし、
談合もなしに、同じ数学のジャンルで、同じ研究をしていたことを 不思議 に思ったからです。
ライプニッツ の 微分積分、関 孝和 も 微分積分 そして 建部賢弘 は テイラー 展開 と
摩 訶 不 思 議
 対 数 e の 素 晴 らしさ
対 数 e の 素 晴 らしさ
対数 e の 発見 は特に 高等数学 の 世界でその 発 展 に大きな 威力を発揮しました
e = 2.71828 18284 59045 鮒 一鉢二鉢 一鉢二鉢 至極 美味しい
★ 指 数 関 数 y = ex は 微分しても積分しても同じ形となる めずらしい関数です
dy / dx = ( ex )’ = ex ∫ex d x = ex ( + C = 0 )
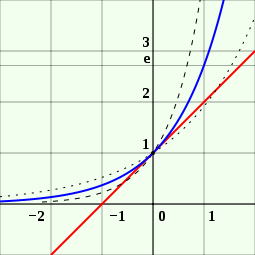
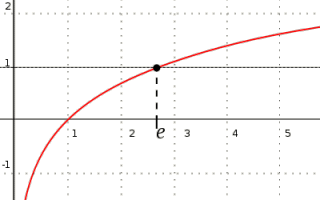
関数 y = ex の グラフ y = log e x の グラフ
★ オイラー の 公 式 e i θ = cos θ + i sin θ
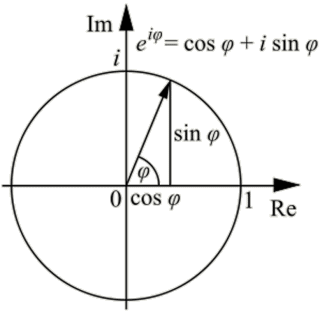

複素数平面 極座標表示 オイラー
この公式は、ロジャー.コーツ によって1714年に提出されたが、その証明は曖昧だった。
その後 オイラー によって1748年に再発見され、有名になったという。
ノーベル物理学賞受賞者 リチャード.ファインマン はこの 公式 を評して
「我々の至宝 」 かつ 「すべての数学のなかでもっとも素晴らしい公式 」 だと述べている。
★ オイラー の 等 式
e π i = - 1 , e π i - 1 = 0
e i θ = cos θ + i sin θ において θ = π のとき
= cos π + i sin π = (cos π =-1) + i (sin π =0) = -1 + i .0
e π i = ( 無理数 ) の( 無理数×虚数 ) 乗 = ー1 = 実 数
数学者 堀場芳数 さんによれば e π i = - 1
「 e イイ オッ π の i 人 アイジン は ただ 1 人 」 という
e .π .i の 「 三 角 関 係 」



時間をかけて 資料 集め しました。 少しは 頭の体操 になったでしょうか
この ぺーじ の Top へ