

���E���� �� �O���t�E�} �`
H�E24�E8�@ Up�@�@ s - 44
�@�@�@�� �� �E �� �� �� �O���t �E �} �` �� ���Ă݂�� �� �� �I �� �� �� ���₷���B
�� �@�� ���@�@��n�@�G�@��2�@�@��3�@�@��4�@�@��5�@�@��6�@�@��7�@�@��8�@�@��9�@�@��10
�@�@�@�@�@�@�@��1�@���@1.000�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@ ��6�@���@2.449�@�@�@�Q�l��ǂ�
�@�@�@�@�@�@�@��2�@���@1.414�@�@������@�@�@�@�@�@�@�@��7�@���@2.645�@�@�@���C�Ŏ����@�@�@
�@�@�@�@�@�@�@��3�@���@1.732�@�@�l���݂��@�@�@�@�@�@�@�@��8�@���@2.828�@�@�@�ɂ�ɂ�
�@�@�@�@�@�@�@��4�@���@2.000�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��9�@���@3.000�@�@�@
�@�@�@�@�@�@�@��5�@���@2.236�@�@�x �m �R �[�@�@�@�@ �@�@�@��10���@3.162�@�@�@�O�F
�@�@�@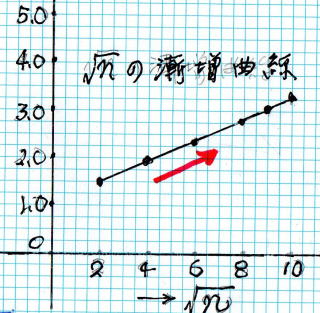 �@�@ �@�@�@�@�@�@�@�@�@�@�@
�@�@ �@�@�@�@�@�@�@�@�@�@�@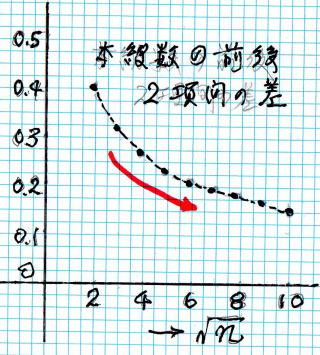
�@ ��1 = 1.000�@��3 = 1.732�@��10 = 3.162�@�@�@�@�@ �@�@�@�@��2-��1 = 0.414�@��10-��9 = 0.162
�@�@�@�@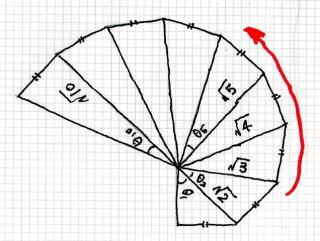 �@
�@  �@�@
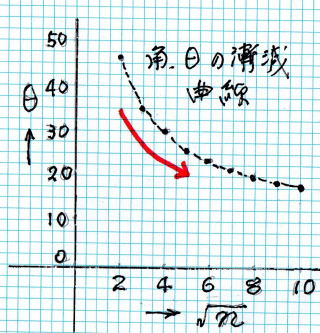
�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�I�I���@�L�@�@�Ɂ@��������
�@�@�s�^�S���X �� �� �� �� ��n �������ɂł���@�@sin��1�@=�@1/�� 2 �@=�@0.71 �@��1�@= 45���@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@���Ȃ݂ɁA�� �� �� �� �a �����߂Ă݂��
�@�@�@�@�@�@����n�� ��1 + ��2 + ��3 + �E�E�E�E�E�E + ��9 + ��1 0 �� 22.466
�@�@�@������������������������������������������������������������������������������������������������������
���@�@�t�B�|�i�b�`���� �E������ �E������@�ɂ��Ă� �} �`
�@�@�����ł́A������ �� �� �� ���� �t�B�|�i�b�`���� �� �W �� �[���̂� �O �� �ɒu��
�@�@�@�@�@�@�@ �@�@������� ���܂��E �v���~�A�� �Ƃ��܂����B
�@�@���@�t�B�|�i�b�`�� ���@�@�@�@�@( 10 �N�O �� �ڂ����@�t�B�|�i�b�`���� )�@�Q ��
�@�@�@�@�@�� ���@ �G�@�@ 1 �E 1 �E 2 �E 3 �E 5 �E 8 �E 13 �E 21 �E 34 �E 55 �E 89 �E 144
�@�@�@�@�@�@�@�@�@�@���́@�� �� �� �����@�@�E�c�M�@�Y�@(�Z)�@�� �� �� �� �� ���܂�
�@�@�@�@�@�@�@�@�@�@�ЂƂ����@�́@�A�T�M�@�� �� �� �ЂƂ��� �� �E�T�M �� �Y ��
�@�@�@�@�@�@�@�@�@�@�������A�Y�܂ꂽ�@�E�T�M�� 2� �� �� ���� �Y �� �͂��߂�
�@�@�@�@�@�@�@�@�@���́@�ЂƂ����@�� �E�T�M �� �Ȍ� �Y�܂�Ă��� �E�T�M �� ������
�@�@�@�@�@�@�@�@�@��N�� �ɎY�� ������ �́@Total 144�@�����@�ƂȂ�܂�
�@�@�@�@�@�@�@�@�@�����āA�y �e �� �� �Y�܂����� �� �z �� ���ׂ� �� ��L �� �� ���ł��܂�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�y �t�B�|�i�b�`���� �� �� �� �z
�@�@�@�@�@�@�@��� �ȍ~ �� �e�� �� ��s����@��� �� �� �� �a�@�ɂ���� �����邱��
�@�@�@�@�@�@�@�@�@�@�@1 + 1 �� 2�@ �@1 + 2 �� 3�@ �@2 + 3 �� 5�@�[�[�[�[�[
�@�@�@�@�@�@�@�@�@�@�� n �� �̃t�B�|�i�b�` �� ���@ Fn �@�Ƃ���Ɓ@�@�@�@
�@�@�@�@�@�@2�� �� �������� ������ �Q�����@ �@Fn�� Fn-1 + Fn-2�@�@�ƕ\����
�@�@�@�@�@�@�@�@�@�@F2 �� F1 + F0�@ �@F3 �� F2 + F1 �@�@F4 �� F3 +F2�@�|�|�|�|
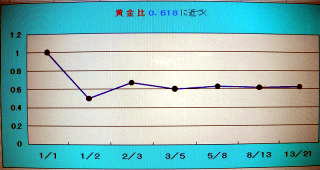
�@�@�@�@�A�@�@������ �� �� �ׂ荇���@�� �́@�� �� ������ 0.618�@ �� �߂Â��� ����
�@�@�@�@�@�@�@�@�@�@�@1 / 1 �E�@1 / 2 �E�@2 / 3 �E�@3 / 5 �@�|�|�@(��5�|1)
/ 2 �� 0.618�@�@
�@�@ �@�@�@ �@
�@�@�@ �@ �@�@�@�@
�@�@�@�@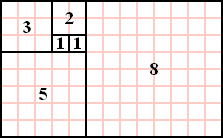
�@�@�@�@�@�@�t�B�|�i�b�`�����́@1202�N �� �t�B�|�i�b�` ���s�@�� �w �Z�Ԃ̏� �x �� ����
��������������������������������������������������������������������������������������������������
�@�@�@�@���@�@�� �� ���@�@�@�@�@�@�@ �@�@(�@1�@0�N�O�@�Ɂ@�ڂ����@������ )�@�Q ��
�O �L�A�t�B�|�i�b�`�����ɂ����ėׂ荇�� 2 �� �� �� �� �� �������E 1.618�@�ɋ߂������Ƃ�g����
�@�@�@�@�@�@�@�@�@������ �� �| �p�� �� �E �� �� �� �� �ÓT�I �� �z�� �@�Ƃ�����
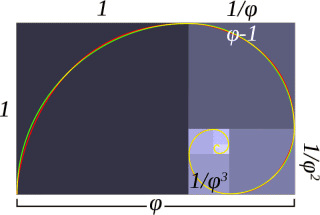
�@�@�@�@�@�@�@�@�@�y �� �� ��@�� �� �z�@�� �W�߂� �݂܂��@�@��������@�lj�
�@�t�B�|�i�b�` �����@�������@�́@�|�p �� ���E �� �� ���R�E �� ���@�E �A�@���� ���E�����鏊��
�@�@�@�@�@�@�@�@�@�@�@�@�@�� ����܂�
�@ �@�@�@�@�@
�@�@�@�@�@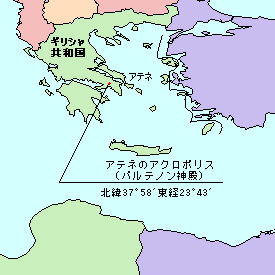 �@�@�@�@�@
�@�@�@�@�@
�@�@�@�@�p���e�m�� �_ �a�@�@�@�@�@�@�� �M���V�� �A�e�l�@�@�@�@�@�@���J�~�G�@���E�����������
�@ �@�@�@�@�@
�@�@�@�@�@ �@�@�@�@�@
�@�@�@�@�@
�@�@�@�@�@�@�s���~�b�h�@�@�@�@�@�@�@�@�@�@�@�@�@�@�K�@ �N�@�@�@�@�@�@�@�@�@�@�@�@�@�@�I�I���K�C
 �@�@�@�@
�@�@�@�@ �@�@�@�@�@�@
�@�@�@�@�@�@1.jpg) �@�@�@�@�@
�@�@�@�@�@
�@�@�@�@���@�� �� ���@���@�@�� ��
�@ �@�@�@�@ 
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� ���@�@2���@�R �s�[�@�q ���@���̂܂�
�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@
�@�@�@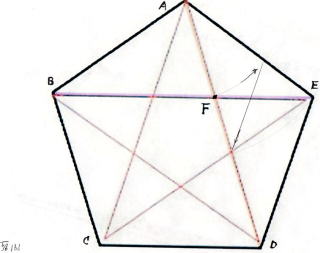
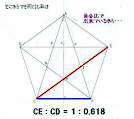
�@�@�@�@�@�@�@�@�@�@�@�@�� �� �����`�@�@�@�@�@�� 5 �p�` �� ��� �� �Ίp�� �� �� �� �� �� ��
�@�@�@�@�@�@�@���@�� �� �����` �ł� �� ��
�@�@�@�@�@�@�@�@�@�@��ӂ̒����@1�@�́@a �Eb �Ec �Ed�@�� �����`
�@�@�@�@�@�@b - c�@�� ���_ �@o�@�� ���S�� ���a�@o - d �� �~ �� ��`�� b - c �� �������� �� e �_
�@�@�@�@�@�@�@�@�@od2 �� (1/2)2 + 12 �� 1/4 + 4/4 �� 5 / 4�@�@�@���@od �� ��5 / 2
�@�@�@�@�@�@�@�@�@ab �Fbe �� ���� �F (bo + oe) �� 1 �F �o1 + �i��5�j/2�p �� 1 �F 1.618
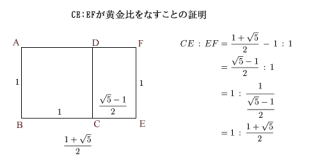
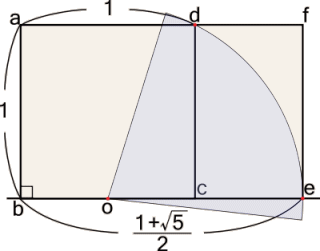
�@�@�@�@�@�@�@���@�� 5 �p �` �ł� �� ���@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@��ӂ̒����@1�@�Ίp�� �� �����@x�Ƃ���
�@�@�@�@�@�@�@�@�@�@�@�@�@���@AFE ���@ADF�@�� �� �� �Ȃ̂�
�@�@�@�@�@�@�@�@�@AF �F AE �� AE �F AD �@�@AF �� ( AD-FD ) �� ( x- 1 )�@�@�@ AE �� 1�@�@ AD �� x
�@�@�@�@�@�@�@�@ ( x- 1 ) �F 1 �� 1 �F x�@�@�@�@( x- 1 ) �E x �� x2 - x �� 1�@�@�@�@ x2- x - 1 �� 0
�@�@�@�@�@�@�@�@�@���́@2�������������@�@x�� �o 1+ ��(1 + 4) �p / 2 �� (1+��5) / 2 �� 1.618
�@������������������������������������������������������������������������������������������������
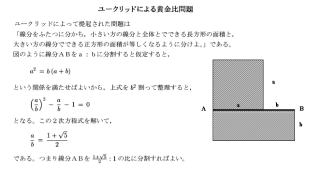
�@�@�@�@���@�@�� �� ���@�� �A�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ȉ��A���ꂼ��@2�������� �� �� �Ƃ��� �^������
�@�@�@�@�@�@�@�� �� ���@�@x2 - x - 1 �� 0�@�@�@�@1�@�F�@( 1 + ��5 ) / 2�@�@�@�@�@�� �� �� �� ��
�@�@�@�@�@�@�@�� �� ���@�@�@x2 - 2x - 1 �� 0�@�@ �@1 �F ��2 �@�@�@�@�@�@�@�@�@�@�@�� �j �� �� ��
�@�@�@�@�@�@�@�� �� ���@�@�@x2 -3x - 1 �� 0�@�@�@�@1 �F �o ( 3 + ��13 ) �p / 2�@�@ �� �O �� �� ��
�@
�@�@�@�@�@�@�@�@�@�@�@���@�@�� �� ���@�ɂ���
�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �� �� 2 �� ����܂�
�@�@�@�@�@�@1�@�@�@1�@�F�@1�@+�@��2�@�@�@�@�@�M���� �� �� �ЂƂ@(�� �� �M���� ��)�@
�@�@�@�@�@�@2�@�@�@1�@�F�@��2�@�@�@�@�� �� ���@ �Ȃǂɗp�����A���{�ł� �Â����� �������� �Ƃ����
�@�@�@ �@�@�@�@
�@�@�@�@
�@�@�@�@�@�@�@�@�@ �� ���@�@�� �d ���@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� ��
�� �� �t
�@�@�@�@�@�@�@�@�@�@�@�@�@�@���j�I �� �� �ɂ� ������ ���� �� �a �� �� �Ă��
�@�@�@�@������������������������������������������������������������������������������������������������
�@���@�� ��@�G�@�� ���@log10 n �@�� �O���t ��
�@�@�@�@�@�@�@�@�@�@�@�@�A ���A�@�@�� �@���@ 1 �E 2 �E 3 �@��[�[�@10�@�@�́@�� �R ���@�Ƃ���
�@���� �� �� ���@�����V �с@�E�@�� �� �� �� ��( �F �m �ǁA�s �� �� �\�h ) �Ȃ̂� �� �� �� �W �J ��
�@�@�@�@�����āA�� �� ������ �� �g�ݗ��Ă� ����܂�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ł́A�n�߂܂��B
�@�@�@�@�@�@�@log10 n�@�@ n �� 1�@����@ n �� 10�@�́@10 �|�C���g �� �O���t�@ �� �` �� �Ƃ�
�@�y �� �� �̑��z �Ȃ̂� �ΐ��\ �����Ȃ��ł������ �� �Z �ŋ��� �� �O���t �� �v���b�g ���܂�
�@���́A�K���� �@log101�@�� 0�@�@ log10 2�@�� 0.3�@�@log10 10 �� 1 �@�� �Y�ꂸ �o���� �����̂�
�@�@�@�@�@�@�@�@����� ����� �c �� �� 7�_ �� �� �Z �� ���߂܂��B
log10 n�@�́@ 3 �_ �� �Y�ꂸ �ɂ������Ƃ� �U �� �Ԃ��� �݂܂��ƁA
log101 �� 0 �́@ a0 �� 1�@�@�w���� �� �ΐ��� �� ���E�\ �� �W �ɂ���̂� �o���₷��
log10 2�@�Ɓ@ log10 10�@�́@�@log�@�v �Z�� ��_�I ���� �Ȃ̂� �L �� ���� �����Ȃ�
�@�@�d�C�W �ł́@�f�V�x���@�@db�� 20 log10 a/b�@���悭�g���܂��B
�@�@�@�@�@�@�@�@�Ⴆ�A�@�@�@a/b �� 2 �@�@�@a/b �� 10�@�@�̂Ƃ�
20 log10 2 �� 20�~0.3 �� 6�@�f�V�x��(db) �@�@�@�@�@20 ������10 10 �� 20�~1 �� 20�@�f�V�x��
2�{ �� 6 �f�V�x���@�@�@�@4�{ �� 6 + 6 �� 12 db �@�@�@�@�@�@8�{ �� 6 + 6 + 6 �� 18�@�f�V�x��
10�{ �� 20 �f�V�x���@�@100�{ �� 20 + 2 0�� 40 db �@�@�@1000�{ �� 20 + 20 + 20 �� 60 db
�Ƃ����悤�ɁA�ΐ� �� ���� �ł���@�|���Z �� �����Z �ɒu������ ���A�܂� �� �� �� �傫�� �� ��
�@�@�@�@�R���p�N �g �� �� �� �u������ ���܂��B
�@�@�@�@�� ( ���� ) �� �傫���@�@�@�d�C�M�� �� �傫���@�ł� �@�f�V�x�� �\ ��
�@�@�@�@��s�@ �� �� ��80�f�V�x���A �d�C�M���� 10���{ �� �� �����Ƃ� 100 �f�V�x�� �� �� �� �Ƃ���
�@�@�@�@�@�@�@�@�@�@�@�啪�A�E �� ���܂����@�ł� �{ �� �� �O���t �� �v���b�g �� �߂�܂�
�@�@�@�A�I�@�悸�A�o���Ă��� 3 �_ ( log10 1�E log10 2 �E log10 10 ) �@�� �O���t �� �v���b�g ���܂�
�@�@�@�@�@�@�@���ɁA �c���@7�_�@�� �� �� �v���b�g ���Ă���
�@�@�@�@�@�e�_ �� �� �v �� �� ���@log �� ���� �E �� �� �� ���p ���Ăꂼ��� �_ �� �� �Z �ŋ��߂܂��B
�C�@log10 4�@�Ɓ@log10 8�@�́@�A�@�� ���@log�@�́@�|���Z �� �����Z �ɒu������ ���邱�Ƃ� ���p����@
�@�@log10 4 �� log10 2�~2 �� log10 2 + log10 2 �� 0.3 + 0.3 �� 0.6�@�@�O���t�� 0.6 �� �v���b�g ���܂�
�G�@log10 8 �� log10 2�~2�~2 �� log10 2+ log102+ log10 2 �� 0.3�~3 �� 0.9�@�@�@�v���b�g�@���܂�
�D�@log10 5�@�́@�A�@�� ���@�́@����Z �� �����Z �� �u������ ���邱�Ƃ� ���p���܂��B
�@�@�@log10 5 �� log1010/2 �� log10 10 - log10 2 �� 1 - 0.3 �� 0.7�@�@0.7�@���@�v���b�g�@���܂�
�B�@log10 3�@�́@3�@�� �f �� �� �|���Z�E ����Z �� �� �� �ł��Ȃ��̂� �O �� 2 �_ ��� �� �v ����B
�@�@log10 3�@�́@ log10 2�@�Ɓ@ log10 4 �@�� �� �� �ɂ���̂� ���ϒl ���藝 �E �z���@ �� ���v����B
�@�@log10 3 �� (log10 2 �{ log104) / 2 �� (0.3 + 0.6) / 2 �� 0.45�@�@�@�@���@0.47
�@�@�O���t �� �� �� �ł������ 0.45 �ł悢�����܂ł� �v���b�g ���� �O���t �� �S �e �������
�@�@�@���A����@���@�� �` �����Ă���B �����ŁA�� �� �q �� + �� ���� 0.47 �Ƃ���B
�@�@�@�@�@�@�Q�@�l�@�@�@�@�@���}�@ ( Interpolation ) �@�E�@�O�}�@ ( Extrapolation )
�@�@����A���@����@�Ȑ��@�� �Ł@�f�[�^ �� ���� �������� ������Ƃ��A ���� �f�[�^ ��
�@�@�@�@�@�@�@�@�@�@�@�@����A����l �����߂�
�@�@�@�E�@log106 �� log10 2�~3 �� log10 2 + log10 3 �� 0.3 + 0.47 �� 0.77
�@�@�@�H�@log109�� log10 32 �� 2 log10 3 �� 2�~0.47 �� 0.94�@
�@�@�@�F�@log10 7�@�́@log103 �� �� �l �Ɂ@3 �� �f �� �Ȃ̂� �O �� �� 2�_ �@log10 6 �@log10 8�@��萄�v
�@�@�@�@�@�@�@�@�@log10 7�� (log10 6 + log10 8) / 2 �� (0.77 + 0.9) / 2 �� 0.83
�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�ȏ� �� 10 �_ �v���b�g �ł��܂���
�@�@�@�@�@�@�@�@�@�@�@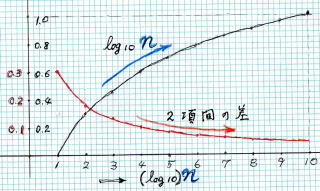
�@�@�@�@�@�@�@�@�@�@�@�@�@�y ���ꂢ���@�O���t�@�@���@�` ���@���Ƃ� �ł��܂��� �z
�@�@�@�@�@�@�@�@�@�@�@�@�@���V�сA���� �� �� �� �I���܂�
�@�@�@�@�@�@�@�@�@�@ �@�@�@�����y�[�W ���s�����@��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2014�@11�@12�@�@�@�@Input Test